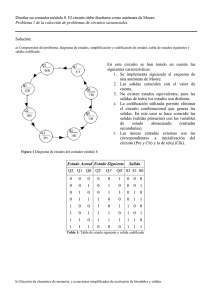
Universidad Tecnológica Nacional Facultad Regional Tucumán Técnicas Digitales I – Departamento Electrónica MÁQUINAS DE ESTADO Un circuito secuencial es aquel cuyas salidas son función, tanto de las salidas, como de la evolución anterior del circuito. O sea, decimos que estos circuitos tienen memoria, identificada en los biestables. Si un circuito tiene n biestables, cada valor concreto de los biestables define un estado del sistema. Un circuito con n biestables tiene 2n estados. Un circuito en estas condiciones puede tener cualquier estructura, pero siempre se podrá llevar al modelo de Moore (introducido por E. F. Moore), o Mealy (introducido por G. H. Mealy). Una máquina de Moore tiene la siguiente estructura: Con n variables de entrada, m bits de salida, por lo tanto 2 m estados y p variables de salida. Su diagrama de estados se representa de la siguiente forma: Donde Ei es el nombre del estado, Zi es la salida que corresponde a dicho estado y Xi la entrada que provoca el salto a otro estado. La máquina de Mealy difiere de la de Moore en que las salidas no son solo función del estado de la máquina, sino también de las entradas. Su modelo y el diagrama de flujo son los siguientes: Igual que en el caso anterior E0 es el nombre del estado, Xi la entrada que provoca el salto a otro estado, y Zi es la salida que corresponde a dicho estado cuando la entrada es X i. Como las salidas dependen de las entradas, una determinada salida estará asociada a la entrada correspondiente. 1 Prof. Ing. Ramón A. Oris Universidad Tecnológica Nacional Facultad Regional Tucumán Técnicas Digitales I – Departamento Electrónica Una consecuencia es que en una máquina de Moore las salidas son síncronas, es decir, solo cambian en los flancos de reloj. En cambio, en las máquinas de Mealy cambiarán con las entradas, es decir en cualquier instante. Cualquier circuito se podrá diseñar con cualquiera de las dos estructuras. De hecho siempre se puede convertir una estructura Moore en una de Mealy y a la inversa. Sin embargo uno de ellos puede ser más simple que el otro. Generalmente una estructura de Mealy suele presentar circuitos más simples. Los contadores síncronos que se estudiaron son un caso particular de máquinas de Moore, por lo tanto el procedimiento de diseño ya es conocido. El único paso que ofrece dificultad es la interpretación del problema planteado, hasta llegar a un diagrama de estados y transiciones que realice lo que plantea el enunciado. Este es el único paso para el que no se puede establecer reglas o procedimientos. Ejemplo 1 Diseñar un autómata de Moore, capaz de detectar 3 o más “1” consecutivos en una entrada serie. a) Diagrama de estados y transiciones Se sugiere, para empezar, identificar una situación estable, o de reposo, y comenzar por dicho estado que llamaremos E0. Aquí está claro cuál es: la situación en que esperamos el primer bit. Identifiquemos este estado con: E0 Espera_Primer_bit Si ahora llega el primer bit por la entrada, y este es un “0”, según el enunciado no tenemos que hacer nada, seguiremos esperando el siguiente como si fuese el primero. Ya tenemos el primer estado y la primera condición de salto. Naturalmente la salida debe ser “0”. Solo será “1” cuando detectemos 3 “unos” seguidos. Si los siguientes son “0”, seguiremos estando aquí. Si llega el primer “1”, la salida seguirá siendo “0”, y aquí llega la primera decisión: ¿podemos quedarnos en este estado, o tenemos que pasar a un nuevo estado? Solo hay una forma de averiguarlo: plantear ambas posibilidades y “ver si funciona”. Veamos: 2 Prof. Ing. Ramón A. Oris Universidad Tecnológica Nacional Facultad Regional Tucumán Técnicas Digitales I – Departamento Electrónica • Cuando llega el primer “1” la salida sigue siendo “0”, correcto. • Llega el segundo “1” y la salida sigue siendo “0”, correcto. • Llega el tercer “1” y la salida sigue siendo “0”, no es correcto. Se ve fácilmente que cuando llega el primer “1” ha de cambiar a otro estado. También se intuye que desde este, si el siguiente es también “1” habrá que saltar a otro estado, etc. El segundo estado podría llamarse: No es difícil deducir que si estando en este estado, llega un “0” volveríamos a E0, y todo vuelve a comenzar. Se nos vuelve a plantear la disyuntiva: si llega el segundo “1”, ¿volvemos a este mismo estado hemos de saltar a otro nuevo? Podemos probar a quedarnos pero se ve fácilmente que hay que saltar a otro estado que llamaríamos: Y a un tercero lo llamaríamos: En E3 la salida es “1”, como dice el enunciado. Si en E3 llega otro “1”, el cuarto, seguiremos en el mismo estado, puesto que el enunciado dice que la salida será “1” cuando se presenten 3 o más unos consecutivos. Una vez alcanzado este punto conviene someter el diagrama a todo tipo de test frente al enunciado, para estar seguros que es coherente, y no nos hemos olvidado ninguna condición. Un test muy sencillo es mirar el diagrama de estado y transiciones, y confirmar que de cada uno de los estados salen tantos grafos como condiciones de entrada haya. Dos en nuestro caso, puesto que hay una sola entrada, 4 si hubiese 2 entradas etc. También es inmediato comprobar que no hay estados en los que “se caiga”, pero nunca se pueda salir. b) Codificación de estados y salidas Se trata de asociar el nombre del estado al valor de los biestables, y al valor de la salida. 3 Prof. Ing. Ramón A. Oris Universidad Tecnológica Nacional Facultad Regional Tucumán Técnicas Digitales I – Departamento Electrónica Estado E0 E1 E2 E3 Codificación Q1 Q0 0 0 0 1 1 0 1 1 Salida Z 0 0 0 1 c) Funciones de salida Normalmente habrá varias salidas. Se trata de obtener las funciones de las salidas simplificadas. Z=Q0*Q1 d) Tabla de transiciones Esta tabla muestra la evolución del circuito para cada estado, con todas las combinaciones de las entradas. Estado actual E0 E1 E2 E3 Entrada I 0 1 0 1 0 1 0 1 Estado siguiente E0 E1 E0 E2 E0 E3 E0 E3 e) Tabla de excitación Es la tabla de las excitaciones de los biestables considerados, según los valores de las salidas antes de la conmutación, Q y después de ella, Q*. 4 Prof. Ing. Ramón A. Oris Universidad Tecnológica Nacional Facultad Regional Tucumán Técnicas Digitales I – Departamento Electrónica f) Funciones de excitación Son las funciones simplificadas que relacionan las excitaciones de los biestables considerados, con las entradas de nuestro circuito y las salidas de los biestables, obtenidas de la tabla anterior. g) Implementación Ejemplo 2 Diseñar un autómata de Mealy, capaz de detectar 3 o más “1” consecutivos en una entrada serie. a) Diagrama de estados y transiciones 5 Prof. Ing. Ramón A. Oris Universidad Tecnológica Nacional Facultad Regional Tucumán Técnicas Digitales I – Departamento Electrónica b) Codificación de estados y salidas Se trata de asociar el nombre del estado y las entradas al valor de los biestables, y al valor de la salida. c) Tabla de transiciones y Funciones de salida Esta tabla muestra la evolución del circuito para cada estado, con todas las combinaciones de las entradas. Puede haber varias salidas. Se trata de obtener las funciones de las salidas simplificadas. ̅̅̅̅𝑄0 + 𝐼𝑄1𝑄0 ̅̅̅̅ = 𝐼(𝑄1 𝜃 𝑄0) 𝑍 = 𝐼𝑄1 d) Tabla de excitación Es la tabla de las excitaciones de los biestables considerados, según los valores de las salidas antes de la conmutación, Q y después de ella, Q*. 6 Prof. Ing. Ramón A. Oris Universidad Tecnológica Nacional Facultad Regional Tucumán Técnicas Digitales I – Departamento Electrónica e) Funciones de excitación Son las funciones simplificadas que relacionan las excitaciones de los biestables considerados, con las entradas de nuestro circuito y las salidas de los biestables, obtenidas de la tabla anterior. f) Implementación Bibliografía Martin Sergio, Castro Manuel E, Acha Santiago, Riosera Miguel A. (2015). Electrónica Diigital. Naucalpan, México: ALFAOMEGA GRUPO EDITOR S.A. 7 Prof. Ing. Ramón A. Oris