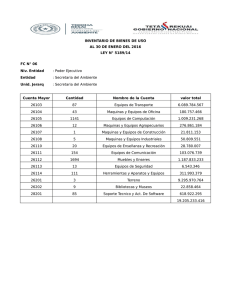
DISEÑO DE ELEMENTOS DE MAQUINA T1. RESISTENCIA A LA FATIGA ANEXO 1: Tablas y figuras M. en C. JOSÉ JAZÁN AVENDAÑO ZÁRATE TABLA A1.1 Resistencia determinísticas mínimas a la tensión y a la fluencia ASTM de algunos aceros laminados en caliente (HR) y estirados en frío (CD) [Ref. 1.2] DISEÑO DE LEMENTOS DE MAQUINAS 2 M. en C. José Jazán Avendaño Zárate 3 DISEÑO DE LEMENTOS DE MAQUINAS TABLA A1.2 Valores de KIC de algunos materiales de ingeniería a temperatura ambiente. M. en C. José Jazán Avendaño Zárate DISEÑO DE LEMENTOS DE MAQUINAS 4 TABLA A1.3 Valores para la constante de Neuber para aceros. TABLA A1.4 Valores para la constante de Neuber para aluminio recocido TABLA A1.5 Valores para la constante de Neuber para aluminio endurecido. M. en C. José Jazán Avendaño Zárate DISEÑO DE LEMENTOS DE MAQUINAS 5 𝑇𝑐 𝜏𝑜 = 𝐽 𝜋𝑑 4 𝐽= 32 Fig. A1.1 Barra redonda ranurada en torsión [Ref. 1.2] M. en C. José Jazán Avendaño Zárate DISEÑO DE LEMENTOS DE MAQUINAS 6 Fig. A1.2a Sensibilidad a la muesca (q) sometidos a flexión inversa de cargas axiales inversas. Para radios de muescas más grandes, use los valores de q correspondiente a la ordenada r=0.16 plg (4mm) [Ref. 1.2] M. en C. José Jazán Avendaño Zárate DISEÑO DE LEMENTOS DE MAQUINAS 7 Fig. A1.2b Sensibilidad a la muesca de materiales sometidos a torsión inversa. En el caso de radios de muescas más grandes use los valores de 𝑞𝑐𝑜𝑟𝑡𝑎𝑛𝑡𝑒 correspondientes a la ordenada 𝑟 = 0.16 𝑝𝑙𝑔 4 𝑚𝑚 [Ref. 1.2] M. en C. José Jazán Avendaño Zárate 8 DISEÑO DE LEMENTOS DE MAQUINAS FIGURA A1.3 Grieta transversal excéntrica en una placa a tensión longitudinal. Curvas continuas corresponde a la punta de la grieta en A, curvas discontinuas son para la punta de la grieta en B. M. en C. José Jazán Avendaño Zárate 9 DISEÑO DE LEMENTOS DE MAQUINAS FIGURA A1.4 Grieta en el borde de una placa a tensión longitudinal. Curva continua no tiene restricción para la flexión, curva discontinua se obtuvo agregando restricciones a la flexión. M. en C. José Jazán Avendaño Zárate 10 DISEÑO DE LEMENTOS DE MAQUINAS FIGURA A1.5 Vigas de sección transversal rectangular con grieta transversal en el borde. M. en C. José Jazán Avendaño Zárate DISEÑO DE LEMENTOS DE MAQUINAS 11 FIGURA A1.6 Placa en tensión que contiene un agujero circular con dos grietas. M. en C. José Jazán Avendaño Zárate DISEÑO DE LEMENTOS DE MAQUINAS 12 FIGURA A1.7 Cilindro sometido a tensión axial, con grieta radial de profundidad, que se extiende por completo alrededor de la circunferencia del cilindro. M. en C. José Jazán Avendaño Zárate 13 DISEÑO DE LEMENTOS DE MAQUINAS FIGURA A1.8 Cilindro sometido a presión interna r, con una grieta radial en la dirección longitudinal y profundidad a. M. en C. José Jazán Avendaño Zárate DISEÑO DE LEMENTOS DE MAQUINAS 14 FIGURA A1.9 Determinación del valor de concentración de esfuerzos para una sección elíptica M. en C. José Jazán Avendaño Zárate DISEÑO DE LEMENTOS DE MAQUINAS 15 FIGURA A1.10 Gráfico para determinar la constante de Neuber para acero y aluminio M. en C. José Jazán Avendaño Zárate DISEÑO DE LEMENTOS DE MAQUINAS 16 FIGURA A1.11 Curvas de sensibilidad a la muesca para aceros M. en C. José Jazán Avendaño Zárate DISEÑO DE LEMENTOS DE MAQUINAS 17 FIGURA A1.12 Curvas de sensibilidad a la muesca para aluminios con tratamiento térmico M. en C. José Jazán Avendaño Zárate DISEÑO DE LEMENTOS DE MAQUINAS 18 FIGURA A1.13 Curvas de sensibilidad a la muesca para aluminio recocido y deformado en caliente. M. en C. José Jazán Avendaño Zárate 19 Sensibilidad a la muesca. DISEÑO DE LEMENTOS DE MAQUINAS Los materiales tienen diferente sensibilidad a la concentración de esfuerzos, lo cual se conoce como sensibilidad a la muesca del material. Cuanto más dúctil sea el material, tendrá menos sensibilidad a la muesca, los materiales frágiles son mas sensibles a la muesca. La sensibilidad a la muesca también depende del radio de la muesca, conforme se aproximan a cero disminuye la sensibilidad a la muesca de los materiales y también se aproximan a cero. M. en C. José Jazán Avendaño Zárate 20 Neuber hizo el primer estudio metódico de los efectos de la muesca y publicó una ecuación para el factor de concentración de esfuerzos de fatiga en 1937. Kuhn revisó más tarde la ecuación de Neuber y desarrollo datos experimentales para la constante de Neuber (propiedad del material)- Peterson refinó posteriormente el procedimiento y desarrollo el concepto de sensibilidad a la muesca q. DISEÑO DE LEMENTOS DE MAQUINAS K f −1 q= Kt −1 Donde Kt es el factor de concentración de esfuerzos teóricos (estático) de la geometría particular y Kf es el factor de concentración de esfuerzo por fatiga (dinámico). La sensibilidad a la muesca q varía entre 0 y 1. K f = 1 + q(K t − 1) M. en C. José Jazán Avendaño Zárate 21 Primero se determina la concentración de esfuerzos teóricos Kt para la geometría y carga en particular, posteriormente se establece la sensibilidad a la muesca adecuada para el material seleccionado con el fin de obtener el factor de concentración de esfuerzos dinámico Kf. El esfuerzo dinámico nominal para cualquier situación se incrementa, entonces, por el factor Kf para esfuerzos por tensión (Kfs para el esfuerzo cortante). DISEÑO DE LEMENTOS DE MAQUINAS = K f nom = K fs nom La sensibilidad a la muesca q también se puede definir a partir de la formula de Kuhn-Hardrath en términos de la constante a de Neuber y del radio r de la muesca, ambos expresado en pulgadas. q= 1 a 1+ r M. en C. José Jazán Avendaño Zárate DISEÑO DE LEMENTOS DE MAQUINAS 22 M. en C. José Jazán Avendaño Zárate DISEÑO DE LEMENTOS DE MAQUINAS 23 M. en C. José Jazán Avendaño Zárate 24 CASO 2. En voladizo, carga intermedia DISEÑO DE LEMENTOS DE MAQUINAS CASO 1. En voladizo, carga en extremo FIGURA A1.14 Formulas y diagramas para cortantes, momentos y deflexión en vigas M. en C. José Jazán Avendaño Zárate CASO 3. En voladizo, carga uniforme DISEÑO DE LEMENTOS DE MAQUINAS 25 FIGURA A1.14 Formulas y diagramas para cortantes, momentos y deflexión en vigas (continuación …) M. en C. José Jazán Avendaño Zárate 26 DISEÑO DE LEMENTOS DE MAQUINAS CASO 4. En voladizo, carga de momento FIGURA A1.14 Formulas y diagramas para cortantes, momentos y deflexión en vigas (continuación …) M. en C. José Jazán Avendaño Zárate CASO 5. Apoyos simples, carga central DISEÑO DE LEMENTOS DE MAQUINAS 27 FIGURA A1.14 Formulas y diagramas para cortantes, momentos y deflexión en vigas (continuación …) M. en C. José Jazán Avendaño Zárate CASO 6. Apoyos simples, carga intermedia DISEÑO DE LEMENTOS DE MAQUINAS 28 FIGURA A1.14 Formulas y diagramas para cortantes, momentos y deflexión en vigas (continuación …) M. en C. José Jazán Avendaño Zárate CASO 7. Apoyos simples, carga uniforme DISEÑO DE LEMENTOS DE MAQUINAS 29 FIGURA A1.14 Formulas y diagramas para cortantes, momentos y deflexión en vigas (continuación …) M. en C. José Jazán Avendaño Zárate 30 DISEÑO DE LEMENTOS DE MAQUINAS CASO 8. Apoyos simples, carga de momento FIGURA A1.14 Formulas y diagramas para cortantes, momentos y deflexión en vigas (continuación …) M. en C. José Jazán Avendaño Zárate 31 DISEÑO DE LEMENTOS DE MAQUINAS CASO 9. Apoyos simples, cargas idénticas FIGURA A1.14 Formulas y diagramas para cortantes, momentos y deflexión en vigas (continuación …) M. en C. José Jazán Avendaño Zárate CASO 10. Apoyos simples, carga en voladizo DISEÑO DE LEMENTOS DE MAQUINAS 32 FIGURA A1.14 Formulas y diagramas para cortantes, momentos y deflexión en vigas (continuación …) M. en C. José Jazán Avendaño Zárate 33 DISEÑO DE LEMENTOS DE MAQUINAS CASO 11. Un apoyo fijo y el otro simple, carga central FIGURA A1.14 Formulas y diagramas para cortantes, momentos y deflexión en vigas (continuación …) M. en C. José Jazán Avendaño Zárate CASO 12. Un apoyo fijo y el otro simple, carga intermedia DISEÑO DE LEMENTOS DE MAQUINAS 34 FIGURA A1.14 Formulas y diagramas para cortantes, momentos y deflexión en vigas (continuación …) M. en C. José Jazán Avendaño Zárate 35 DISEÑO DE LEMENTOS DE MAQUINAS CASO 13. Un apoyo fijo y el otro simple, carga uniforme FIGURA A1.14 Formulas y diagramas para cortantes, momentos y deflexión en vigas (continuación …) M. en C. José Jazán Avendaño Zárate CASO 14. Apoyos fijos, carga central DISEÑO DE LEMENTOS DE MAQUINAS 36 FIGURA A1.14 Formulas y diagramas para cortantes, momentos y deflexión en vigas (continuación …) M. en C. José Jazán Avendaño Zárate CASO 15. Apoyos fijos, carga intermedia DISEÑO DE LEMENTOS DE MAQUINAS 37 FIGURA A1.14 Formulas y diagramas para cortantes, momentos y deflexión en vigas (continuación …) M. en C. José Jazán Avendaño Zárate 38 DISEÑO DE LEMENTOS DE MAQUINAS CASO 16. Apoyos fijos, carga uniforme FIGURA A1.14 Formulas y diagramas para cortantes, momentos y deflexión en vigas (continuación …) M. en C. José Jazán Avendaño Zárate