Sesión 2 INTERVALO DE CONFIANZA PARA LA MEDIA

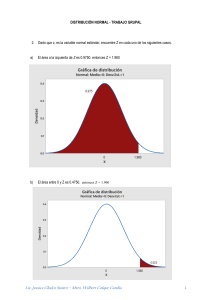
ESTADÍSTICA II
SESIÓN 2: INTERVALO DE CONFIANZA PARA LA
MEDIA DE UNA POBLACIÓN
AUTORES
:
Lic. Jessica Elizabeth Chalco Suárez
:
Mtro. Wilbert Colque Candia
Intervalos de confianza
ESTADÍSTICA II
DISTRIBUCIONES MUÉSTRALES
Una estadística muestral proveniente de una muestra aleatoria simple tiene un patrón de
comportamiento (predecible) en repetidas muestras. Este patrón es llamado la distribución muestral
de la estadística.
Si conocemos la distribución muestral podemos hacer inferencia. Las distribuciones muéstrales
adoptan diferentes formas según las estadísticas investigadas y las características de la población
estudiada.
DISTRIBUCIÓN MUESTRAL DE LA MEDIA
La distribución muestral de la media es la distribución de los valores de las medias muéstrales
de todas las posibles muestras del mismo tamaño n tomadas de la misma población
Si sacamos muestras aleatorias de tamaño n de una población con media μ y desviación estándar σ,
entonces la distribución muestral de la media muestral tiene las siguientes propiedades:
1. El promedio de todos los valores posibles de medias muéstrales es igual al parámetro μ. En otras
palabras, la media muestral x̅ es un estimador insesgado de μ.
μx̅ = μ
2. Error estándar de la media muestral: Es la desviación estándar de las posibles medias
muestrales.
σx̅ =
σ
√n
El error estándar disminuye si el tamaño de la muestra aumenta.
Se puede interpretar como el grado de variabilidad que tiene la media muestral con respecto
a la media poblacional. En otras palabras, es una medida de la incertidumbre que existe al
estimarla media poblacional a partir de la media muestral
3. Si la muestra es obtenida sin remplazo de una población finita de tamaño N, entonces el error
estándar es
σx̅ =
El coeficiente
N−n
N−1
σ
N−n
√
√n N − 1
es denominado factor de corrección para población finita. Se observa que
cuandoN → +∞el factor de corrección tiende a uno.
4. Si la población original tiene distribución Normal, entonces para cualquier tamaño muestral "n"
la distribución de la media muestral es también Normal
Lic. Jessica Chalco Suárez – Mtro. Wilbert Colque Candia
2
Intervalos de confianza
ESTADÍSTICA II
Si
X ~ N(μ, σ) ⇒ x̅ ~ N (μ,
σ
√n
)
5. Si la población de origen no es Normal, pero podemos calcular su media y desviación estándar y
el tamaño muestral (n) es “suficientemente” grande la distribución de la media muestral es
aproximadamente Normal
Aun si X no es N(μ, σ) ⇒ x̅ ~ N (μ,
σ
√n
)
Este resultado se conoce como el Teorema del Límite Central.
TEOREMA DEL LÍMITE CENTRAL
Este es uno de los teoremas más importantes en probabilidad y en general en estadística. Si x̅ es
la media de una muestra de tamaño n que se toma de una población normal con media μ y
x̅−μ
varianzaσ2 entonces la variable Z = σ
tiende a la distribución normal estándar a medida que n
⁄ n
√
tiende a infinito. Es decir:
x̅ − μ (x̅ − μ)√n
Z=σ
=
~ N(0,1)
σ
⁄ n
√
Observación: cuando se desconoce la varianza poblacional y se tiene que estimar a partir de los
datos de la muestra como S 2 =
̅ )2
∑(Xi −X
n−1
x̅−μ
entonces la estadísticaT = s
⁄ n
√
tiene una distribución t
de Student con n –1 grado de libertad.
Lic. Jessica Chalco Suárez – Mtro. Wilbert Colque Candia
3
Intervalos de confianza
ESTADÍSTICA II
INTERVALOS DE CONFIANZA PARA LA MEDIA POBLACIONAL
La estimación de la media poblacional se hace mediante la variable aleatoria Z, así el intervalo de
estimación es:
1.1
Intervalo de confianza para una población infinita
➢ Intervalo de confianza para 𝝁 (𝒏 ≥ 30)
𝐼𝐶(𝜇)(1−𝛼)% : 𝑥̅ − 𝑒 ≤ 𝝁 ≤ 𝑥̅ + 𝑒
𝐼𝐶(𝜇)(1−𝛼)% : 𝑥̅ − 𝑍0 ∗ 𝜎𝑥̅ ≤ 𝝁 ≤ 𝑥̅ + 𝑍0 ∗ 𝜎𝑥̅
𝐼𝐶(𝜇)(1−𝛼)% : 𝑥̅ − 𝑍0 ∗
𝜎
√𝑛
≤ 𝝁 ≤ 𝑥̅ + 𝑍0 ∗
𝜎
√𝑛
Error estandar o desviación estandar = 𝜎𝑥̅ =
𝜎
√𝑛
Con un error máximo de: 𝑒 = 𝑍0 ∗ Error estandar ⟹
𝑍0
𝜎
e = 𝑍0 ∗
√𝑛
Es el valor teórico de la distribución normal estándar, depende del nivel de
confianza(1 − 𝛼)
Nivel de confianza
90%
91%
92%
93%
94%
95%
96%
97%
98%
99%
𝑍0
1,645
1,695
1,751
1,812
1,881
1,96
2,054
2,17
2,326
2,576
➢ Intervalo de confianza para 𝝁 (𝒏 < 30)
𝐼𝐶(𝜇)(1−𝛼)% : 𝑥̅ − 𝑒 ≤ 𝝁 ≤ 𝑥̅ + 𝑒
𝐼𝐶(𝜇)(1−𝛼)% : 𝑥̅ − 𝑡0 ∗ 𝜎𝑥̅ ≤ 𝝁 ≤ 𝑥̅ + 𝑡0 ∗ 𝜎𝑥̅
𝐼𝐶(𝜇)(1−𝛼)% : 𝑥̅ − 𝑡0 ∗
𝑆
√𝑛
≤ 𝝁 ≤ 𝑥̅ + 𝑡0 ∗
𝑆
√𝑛
Error estandar o desviación estandar = 𝜎𝑥̅ =
𝑆
√𝑛
Con un error máximo de: 𝑒 = 𝑡0 ∗ Error estandar ⟹
e = 𝑡0 ∗
𝑆
√𝑛
𝑡0 Es el valor teórico de la distribución T- Student, depende del nivel de confianza(1 − 𝛼)
y los grados de libertad de la distribución. (grado de libertad: 𝜈 = 𝑛 − 1)
1.2
Intervalo de confianza para una población finita
𝐼𝐶(𝜇)(1−𝛼)% : 𝑥̅ − 𝑒 ≤ 𝜇 ≤ 𝑥̅ + 𝑒
𝐼𝐶(𝜇)(1−𝛼)% : 𝑥̅ − 𝑍0 ∗ 𝜎𝑥̅ ≤ 𝜇 ≤ 𝑥̅ + 𝑍0 ∗ 𝜎𝑥̅
𝐼𝐶(𝜇)(1−𝛼)% : 𝑥̅ − 𝑍0 ∗
𝜎
𝑁−𝑛
𝜎 𝑁−𝑛
√
√
≤ 𝜇 ≤ 𝑥̅ + 𝑍0 ∗
√𝑛 𝑁 − 1
√𝑛 𝑁 − 1
Error estandar o desviación estandar = 𝜎𝑥̅ =
𝜎
𝑁−𝑛
√
√𝑛 𝑁 − 1
Lic. Jessica Chalco Suárez – Mtro. Wilbert Colque Candia
4
Intervalos de confianza
Donde√
𝑁−𝑛
𝑁−1
ESTADÍSTICA II
es denominado factor de corrección para poblaciones finitas
Con un error máximo de: 𝑒 = 𝑍0 ∗ Error estandar ⟹ e = 𝑍0 ∗
𝜎
𝑁−𝑛
√
√𝑛 𝑁−1
𝑍0 Es el valor teórico de la distribución normal estándar.
Caso práctico de intervalo de confianza para una población infinita (𝒏 ≥ 𝟑𝟎)
Ejemplo 1
La asociación de productores de azúcar desea calcular el consumo medio de azúcar por año. Una
muestra aleatoria de 75 personas revela que el consumo medio anual es de 12 kilos por persona,
con una desviación estándar de 2.4 kilos. Determine el intervalo de confianza de 95% para la
media poblacional (interprete), es razonable concluir que la media poblacional es de 15 kilos.
Procedimiento 1: (Utilizando calculadora)
Tamaño de la muestra
𝑛=
Media o promedio
𝑥̅ =
Desviación estándar
𝜎=
Error estándar
𝜎𝑥̅ =
Nivel de confianza
1−𝛼 =
𝑍0
Error máximo
𝜎
√𝑛
𝑍0 =
𝑒 = 𝑍0 ∗ 𝜎𝑥̅ =
𝐿𝐼
𝑥̅ − 𝑒 =
𝐿𝑆
𝑥̅ + 𝑒 =
𝐼𝐶(𝜇)1−𝛼% : 𝐿𝐼 ≤ 𝜇 ≤ 𝐿𝑆
=
≤𝜇≤
Interpretación:
Lic. Jessica Chalco Suárez – Mtro. Wilbert Colque Candia
5
Intervalos de confianza
ESTADÍSTICA II
Para calcular 𝑍0
Grafica – Grafica de distribución de distribución probabilidad – Aceptar
Gráfica de distribución
Normal; Media=0; Desv.Est.=1
0,4
Densidad
0,3
0,2
0,1
0,025
0,0
0,025
-1,960
0
X
1,960
El valor de 𝑍0 = 1,96 (solo se considera el valor positivo)
Procedimiento 2: (Utilizando Minitab)
Estadísticas - Estadísticas básicas – Z de una muestra
Lic. Jessica Chalco Suárez – Mtro. Wilbert Colque Candia
6
Intervalos de confianza
ESTADÍSTICA II
Ejemplo 2
Con objeto de estimar la cantidad media que gasta un cliente en un almuerzo, El administrador
del restaurante típico de la región “El sabor de casa”, registro los datos de una muestra de 85
clientes. Suponga que la desviación estándar de la población es S/15. Si la media poblacional es
S/45
a)
¿El error máximo al 90% de confianza?
b)
¿El intervalo de confianza de 90% para la media poblacional?
c)
El Restaurant puede esperar que un cliente gaste en promedio S/70
Solución
𝑛=
𝑥̅ =
𝜎=
1−𝛼 =
Lic. Jessica Chalco Suárez – Mtro. Wilbert Colque Candia
7
Intervalos de confianza
ESTADÍSTICA II
Ejemplo 3
En la ciudad de Cusco se desea conocer las utilidades anuales (Miles de soles) de las empresas
dedicadas al transporte de carga, para lo cual se obtuvo información de una muestra de 60
empresas. Estimar:
a)
¿El error máximo al 99% de confianza?
b)
¿El intervalo de confianza de 99% para la media poblacional?
c)
Una empresa puede esperar una utilidad promedio de S/85
33
53
66
48
35
55
66
68
65
74
67
59
35
42
60
80
41
91
73
64
88
65
76
81
57
77
69
85
59
64
53
85
37
84
73
41
97
61
73
77
58
52
74
45
41
46
55
77
50
65
76
68
30
65
59
76
71
60
98
64
Lic. Jessica Chalco Suárez – Mtro. Wilbert Colque Candia
8
Intervalos de confianza
ESTADÍSTICA II
Caso práctico de intervalo de confianza para una población infinita (𝒏 < 𝟑𝟎)
Ejemplo 4
La oficina de marketing de toda una red de empresas dedicadas a la venta de productos vía online,
está preocupada por la aceptación de sus productos, una muestra aleatoria de 25 llamadas indico
un gasto promedio en compras de S/380 con una desviación estándar de 60 nuevos soles.
a)
Determine el intervalo de confianza de 99% para la media poblacional. interprete
b)
Es razonable concluir que la media poblacional es de S/450.
Procedimiento 1: (Utilizando calculadora)
Tamaño de la muestra
𝑛=
Media o promedio
𝑥̅ =
Desviación estándar
𝜎=
Error estándar
𝜎𝑥̅ =
Nivel de confianza
1−𝛼 =
𝑡0
𝑔𝑙: 𝜈 = 𝑛 − 1 =
Error máximo
𝜎
√𝑛
𝑡0 =
𝑒 = 𝑡0 ∗ 𝜎𝑥̅ =
𝐿𝐼
𝑥̅ − 𝑒 =
𝐿𝑆
𝑥̅ + 𝑒 =
𝐼𝐶(𝜇)1−𝛼% : 𝐿𝐼 ≤ 𝜇 ≤ 𝐿𝑆
=
≤𝜇≤
Interpretación:
Lic. Jessica Chalco Suárez – Mtro. Wilbert Colque Candia
9
Intervalos de confianza
ESTADÍSTICA II
Para calcular 𝑡0
Grafica – Grafica de distribución de distribución probabilidad – Aceptar
Seleccionar la distribución t
Gráfica de distribución
T; df=24
0,4
Densidad
0,3
0,2
0,1
0,0
0,005
0,005
-2,797
0
X
2,797
𝑡0 = 2.797
Procedimiento 2: (Utilizando Minitab)
Estadísticas - Estadísticas básicas – t de una muestra
Lic. Jessica Chalco Suárez – Mtro. Wilbert Colque Candia
10
Intervalos de confianza
ESTADÍSTICA II
Ejemplo 5
Una Empresa quiere ofrecer el servicio de guardería para sus empleados. Como parte del estudio
de viabilidad del proyecto, desean calcular el costo medio semanal por el cuidado de los niños.
Una muestra de 10 empleados que recurren al servicio de guardería revela las siguientes
cantidades gastadas(soles) la semana pasada.
107
110
100
95
107
130
125
150
125
104
Determine el intervalo de confianza de 90% para la media poblacional, Interprete.
Ejemplo 6
Las cajas de un cereal producidos en una fabrica deben tener un contenido de 16 onzas. Un
inspector tomo una muestra que arrojo los siguientes pesos en onzas
15.7
16.3
15.7
15.8
16.1
15.9
16.2
15.9
15.8
15.6
Indicar si es razonable que el inspector usando un coeficiente de confianza del 95% ordene que
se multe al fabricante.
Lic. Jessica Chalco Suárez – Mtro. Wilbert Colque Candia
11
Intervalos de confianza
ESTADÍSTICA II
Ejemplo 7
La secretaría de admisiones en un programa de máster en administración de empresas ha
observado que los solicitantes tienen una calificación media en los estudios que se distribuyen
normalmente con una desviación típica de 1,95. Se ha extraído una muestra aleatoria de 27
solicitudes cuya calificación media ha resultado ser 15,90.
a)
Halle el intervalo de confianza de la media poblacional al 99 por ciento.
b)
Basándose en estos resultados muestrales, un estadístico calcula para la media poblacional
el intervalo de confianza que va de 15,18 a 16,62. Halle el nivel de confianza
correspondiente a este intervalo.
Ejemplo 8
Se obtiene una muestra de edades de 20 estudiantes de una escuela nocturna, la edad media de
estudiantes de escuelas nocturnas. 𝑋̅ = 25.3 años. La varianza de la población es 16.
a)
El margen de error al 95%
b)
Encuentre el intervalo de confianza de 95% para 𝜇.
c)
El margen de error al 99%
d)
Encuentre el intervalo de confianza de 99% para 𝜇.
Lic. Jessica Chalco Suárez – Mtro. Wilbert Colque Candia
12
Intervalos de confianza
ESTADÍSTICA II
Caso práctico de intervalo de confianza para una población finita
Ejemplo 9
El ingreso mensual de 600 microempresas de metal mecánica de la ciudad del Cusco, se asume es
una variable aleatoria con distribución normal. Obtenga un intervalo de estimación para el ingreso
promedio mensual con un nivel de confianza del 97%, si una muestra de 120 microempresas
escogidas al azar dio una media de S/9540, con una desviación estándar de S/1530.
Procedimiento 1: (Utilizando calculadora)
Tamaño de la población
𝑁
Tamaño de la muestra
𝑛=
Media o promedio
𝑥̅ =
Desviación estándar
𝜎=
Error estándar
𝜎𝑥̅ =
Nivel de confianza
1−𝛼 =
𝑍0
Error máximo
𝜎
𝑁−𝑛
=
√𝑛 𝑁 − 1
√
𝑍0
𝑒 = 𝑍0 ∗ 𝜎𝑥̅ =
𝐿𝐼
𝑥̅ − 𝑒 =
𝐿𝑆
𝑥̅ + 𝑒 =
𝐼𝐶(𝜇)1−𝛼% : 𝐿𝐼 ≤ 𝜇 ≤ 𝐿𝑆
Interpretación:
Lic. Jessica Chalco Suárez – Mtro. Wilbert Colque Candia
13
Intervalos de confianza
ESTADÍSTICA II
Ejemplo 10
Un parque de recreaciones. En el mes de Julio fue visitado 600 familias, el administrador tomo
una muestra de 73 familias y determino que la desviación estándar es de $175 y la media de
gastos por familia fue $332
a)
¿Con 95% de confianza cuál es el margen de error maximo?
b)
¿Cuál es el intervalo de confianza de 95% para estimar la media poblacional?
c)
El administrador puede esperar que el proximo mes las familias gasten en promedio
$500.
Ejemplo 11
Un analista de investigacion de mercado escoge una muestra aleatoria de 140 clientes de un
conjunto 1500, de una gran tienda que declararon ingresos mayores a S/. 7000. El encuentra que
los clientes de la muestra gastaron en la tienda un promedio S/. 960 si con este valor de la muestra
se estima que el gasto promedio de la poblacion finita varia de S/. 929,9 a S/. 990,1 ¿Qué nivel
de confianza se utiliza? Suponga que la desviacion estándar de la poblacion es de S/. 200.
Lic. Jessica Chalco Suárez – Mtro. Wilbert Colque Candia
14