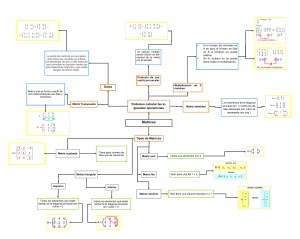
2a. Unidad. Matrices y determinantes.
2.1 Definición de matriz, notación y orden
Definición de MATRIZ: es una tabla cuadrada o rectangular de datos (llamados elementos ó
componentes) ordenados en filas y columnas, donde una fila es cada una de las líneas horizontales de la
matriz y una columna es cada una de las líneas verticales. A una matriz con m filas y n columnas se le
denomina matriz m-por-n (escrito m × n). Las dimensiones de una matriz siempre se dan con el número
de filas primero y el número de columnas después.
NOTACIONES más usuales de matriz son los paréntesis ( ) y los corchetes [
], dentro de los cuales
van los elementos de la matriz.
Comúnmente se dice que una matriz m-por-n tiene un ORDEN de m × n ("orden" tiene el significado
de tamaño). Dos matrices se dice que son iguales si son del mismo orden y tienen los mismos elementos.
O de orden 4, significando de 4 filas y 4 columnas.
Ejemplo:
1
1
Dada la matriz: 𝐴 = [
4
6
La matriz:
𝑅 = [1
2
2
9
0
2 3
3
7
] que es una matriz 4x3. El elemento A [2,3] es el 7
2
5
4 5 6
7 8 9] es una matriz 1 × 9, o un vector fila con 9
elementos.
La matriz:
1
𝐶 = [2] es una matriz 3 × 1, o un vector columna con 3 elementos.
3
2.2 Operaciones con matrices
Las operaciones usuales con matrices, son las siguientes: suma, resta, multiplicación con un
escalar y
multiplicación de matrices.
SUMA
𝑎11
si 𝐴 = [𝑎
21
𝑎12
𝑏11
𝑎22 ] y 𝐵 = [𝑏21
𝑏12
] son matrices del mismo orden, entonces [A]+[B]=
𝑏22
[C]
luego
𝑐11
𝐶 = [𝑐
21
𝐶=[
para
una
𝑐12
𝑐22 ] , si cada uno de ellos es de 2° orden, así:
𝑎11 + 𝑏11
𝑎21 + 𝑏21
suma
𝑎11 + 𝑏11 + 𝑐11
[𝑎21 + 𝑏21 + 𝑐21
𝑎31 + 𝑏31 + 𝑐31
de
𝑎12 + 𝑏12
],
𝑎22 + 𝑏22
matrices
𝑎12 + 𝑏12 + 𝑐12
𝑎22 + 𝑏22 + 𝑐22
𝑎32 + 𝑏32 + 𝑐32
de
3er.
Orden
𝐷=
𝑎13 + 𝑏13 + 𝑐13
𝑎23 + 𝑏23 + 𝑐23 ] y así
𝑎33 + 𝑏33 + 𝑐33
sucesivamente hacia matrices de orden “n”, quedando en el siguiente formato:
𝐷=
𝑎11 + 𝑏11 + ... + 𝑛11
𝑎21 + 𝑏21 + ... + 𝑛21
.
.
.
[𝑎𝑚1 + 𝑏𝑚1 + ... + 𝑛𝑚1
𝑎12 + 𝑏12 + ... + 𝑛12
𝑎22 + 𝑏22 + ... + 𝑛22
.
.
.
𝑎𝑚2 + 𝑏𝑚2 + ... + 𝑛𝑚2
... 𝑎1n + 𝑏1𝑛 + ... + 𝑛1𝑛
... 𝑎2n + 𝑏2𝑛 + ... + 𝑛2𝑛
...
.
...
.
...
.
... 𝑎𝑚𝑛 + 𝑏𝑚𝑛 + ...𝑛𝑚𝑛 ]
RESTA
para la resta de matrices, si [A] y [B] son matrices del mismo orden, entonces [A]-[B]=[C],
donde
𝐶=[
𝑎11 − 𝑏11
𝑎21 − 𝑏21
𝑎12 − 𝑏12
]
𝑎22 − 𝑏22
Multiplicación con un escalar
si k es un escalar y [A] una matriz., entonces k[A], resultando la multiplicación de k por cada
elemento
de la matriz. Quedando para una matriz de 2o. Orden, así:
𝑘 ∗ 𝑎11
𝑘[𝐴] = [
𝑘 ∗ 𝑎21
𝑘 ∗ 𝑎12
]
𝑘 ∗ 𝑎22
Multiplicación de matrices
SI [A] y [B] son matrices teniendo ordenes de m x n y p x q respectivamente.
Luego si n = p, es decir “si el número de columnas de la primera matriz es igual al número
de filas de la
segunda” se puede realizar la multiplicación de matrices, de otra manera no. Resultando el
producto
una matriz de orden m x q.
Si n = p entonces [𝐶]𝑚𝑞
la multiplicación se lleva a cabo de la siguiente forma:
[𝐴][𝐵] = [𝑎11
𝑎12
de orden
𝑎13
𝑏11
𝑏21
𝑎15 ] 𝑏31 = resultando, como:
𝑏41
[𝑏51 ]
𝑎14
1x5
5x1
columnas de [A]:
5 = 5 filas de [B], por tanto si se pueden multiplicar,
luego
𝐶 = [𝑎11 ∗ 𝑏11 + 𝑎12 ∗ 𝑏21 + 𝑎13 ∗ 𝑏31 + 𝑎14 ∗ 𝑏41 + 𝑎15 ∗ 𝑏51 ] = [C11]
de orden 1
filas: 1 x 1 columna, o de un
solo elemento.
Así, una multiplicación de matrices, será:
𝑎
[𝐴] = [𝑎11
si
[
21
𝑎11 ∗ 𝑏11 + 𝑎12 ∗ 𝑏21
𝑎21 ∗ 𝑏11 + 𝑎22 ∗ 𝑏21
de orden
2x2
2 columnas de [A] y
𝑎12
𝑎22 ]
y
𝑏
[𝐵] = [ 11
𝑏21
𝑏12
]
𝑏22
=
𝑎11 ∗ 𝑏12 + 𝑎12 ∗ 𝑏22
]=
𝑎21 ∗ 𝑏12 + 𝑎22 ∗ 𝑏22
2x2
2 filas de [B]. portanto se cumple la condición de columnas
de [A] =
filas de [B], de manera que si se puede efectuar la multiplicación de matrices
obteniendo una matriz de la forma
𝑐
[𝐶] = [𝑐11
21
𝑐12
𝑐22 ] resultando en una matriz de orden 2 x 2. o de 2o. Orden.
Y así, la multiplicación de 2 matrices de orden “n”, resultará:
𝑎11 ∗ 𝑏11 + 𝑎12 ∗ 𝑏21 + ... + 𝑎1𝑛 ∗ 𝑏𝑚1
𝑎21 ∗ 𝑏11 + 𝑎22 ∗ 𝑏21 + ... + 𝑎2𝑛 ∗ 𝑏𝑚1
.
𝐶=
.
.
[𝑎𝑚1 ∗ 𝑏11 + 𝑎𝑚2 ∗ 𝑏21 + ... + 𝑎𝑚𝑛 ∗ 𝑏𝑚1
𝑎11 ∗ 𝑏12 + 𝑎12 ∗ 𝑏22 + ... + 𝑎1𝑛 ∗ 𝑏𝑚2
𝑎21 ∗ 𝑏12 + 𝑎22 ∗ 𝑏22 + ... + 𝑎2𝑛 ∗ 𝑏𝑚2
.
.
.
𝑎𝑚1 ∗ 𝑏12 + 𝑎𝑚2 ∗ 𝑏22 + ... + 𝑎𝑚𝑛 ∗ 𝑏𝑚2
Ejemplos:
6
−7
a) Si A= [1 -2 3 4 5] y B= 8 , encontrar [A]*[B]
9
[0]
entonces C= [1(6) +(-2) (-7) +3(8) +4(9) +5(0)] = [6+14+24+36+0] =
C = [80]
b) Si C=(
1 −2
−5 6
) yD=(
), luego (C)*(D)=(E)
3 4
7 0
...𝑎11 ∗ 𝑏13 + 𝑎12
...𝑎21 ∗ 𝑏13 + 𝑎22
...𝑎𝑚1 ∗ 𝑏13 + 𝑎𝑚
1(−5) + (−2)(7) 1(6) + (−2)(0)
entonces E = (
)
3(−5) + 4(7)
3(6) + 4(0)
−5 − 14
−15 + 28
= (
6−0
−19
) =(
13
18 + 0
6
)
18
2.3 Clasificación de las matrices
las matrices se clasifican en:
Matrices iguales: dadas 𝐴 = [𝑎𝑖 𝑗 ]𝑦 𝐵 = [𝑏𝑖 𝑗 ] , 2 matrices son iguales [a] = [b] si y sólo sí:
A y B tienen el mismo tamaño y
𝑎𝑖 𝑗 = 𝑏𝑖 𝑗 para todo i, j.
Matriz cero: es aquella de tamaño m x n se define como aquella que tiene las m x n
componentes
nulas; esto es.
Ҩ = [𝑎𝑖 𝑗 ] donde 𝑎𝑖 𝑗 = 0 para toda i, j. Asi por ejemplo.
0
Ҩ=[
0
0 0
] Que es la matriz cero 2 x 3.
0 0
Matriz identidad n x n:
1 0 ... 0
0 1 ... 0
1,
. . ... .
𝐼𝑛 =
; es decir, 𝐼𝑛 = [𝑎𝑖 𝑗 ], 𝑑𝑜𝑛𝑑𝑒 𝑎𝑖 𝑗 = {
0,
. . ... .
. . ... .
[0 0 ... 1]
𝑠𝑖
𝑠𝑖
𝑖 = 𝑗;
}
𝑖 ≠ 𝑗.
Así, por ejemplo.
1 0 0
𝐼3 = [0 1 0] Es la matriz identidad 3 x 3.
0 0 1
Matriz fila: 𝐴 = [𝑎11
𝑎12
... 𝑎1n ]
𝑏11
𝑏21
.
Matriz columna: 𝐵 =
.
.
[𝑏𝑚1 ]
Matriz cuadrada: se les llama a las matrices de tamaño n x n de orden n y al conjunto formado
por éstas
se denotará por ℳ𝑛
Diagonal de la matriz: si 𝐴 = [𝑎𝑖 𝑗 ] es una matriz cuadrada de orden n, se dice que los
elementos
𝑎11 , 𝑎22 , 𝑎33 ,..., 𝑎𝑛𝑛 forman o están en la diagonal de la matriz A. Y si 𝐴 = [𝑎𝑖 𝑗 ] pertenece
aℳ𝑚 𝑥 𝑛 .
se dirá que los elementos 𝑎𝑖 𝑗 con i = j forman la diagonal principal de la matriz A.
Si
−1 5
7
3
𝑀=[
3
0
1 −5
0
−1
4
9
2
1
]
2
7
entonces 𝑚11 = −1,𝑚22 = 3,𝑚33 = 4,𝑚44 = 7 son los
elementos de la
diagonal de la matriz cuadrada M.
Matriz triangular superior: es una matriz cuadrada A de orden n, si los componentes que están
por
debajo de la diagonal son todas nulas.
−1
0
𝐴=[
0
0
5 0 2
3 −1 1
]
0 4 2
0 0 7
Matriz triangular inferior: es aquella si las componentes que están por arriba de la diagonal,
son
todas iguales a cero.
−1
−5
𝐵=[
2
6
0
3
0
0
0
0
4
4
0
0
]
0
0
Matriz diagonal: sea A una matriz cuadrada de orden n, si todas las componentes fuera de su
diagonal
son nulas. Si 𝑎𝑖𝑖 = 𝜆𝑖 , i = 1, 2, ..., n. son las componentes de la diagonal de esta matriz se
escribe
𝐴 = 𝑑𝑖𝑎𝑔(𝜆1 , 𝜆2 ,..., λ𝑛 ) para representar a la matriz diagonal A.
4 0 0
La matriz cuadrada [0 3 0] es diagonal. Esto es,
0 0 8
A = diag (4,3,8)
Matriz traspuesta: de A. Si A = [𝑎𝑖 𝑗 ] pertenece a mxn se define como 𝐴𝑡 = [𝑏𝑖 𝑗 ], donde 𝑏𝑖 𝑗 =
𝑎𝑗 𝑖
para i= 1, 2, ..., n y
j = 1, 2. ..., m. De la definición se desprende que 𝐴𝑡 tiene tamaño n x
m y que en
la matriz traspuesta la primera columna es la primera fila de A, la segunda columna es la
segunda fila de
A, etcétera.
1
Si 𝐴 = [
5
2 3
6 7
4
],
8
1
2
𝐴𝑡 = [
3
4
5
6
]
7
8
Matriz simétrica: de A, es cuando 𝐴𝑡 = 𝐴
la matriz 𝐴 = [
−1 2
]
2 3
es simétrica pues claramente 𝐴 = 𝐴𝑡 .
7 8 9
a) obtener la matriz simétrica de 𝐸 = (6 5 4)
1 2 3
E sim
7
= (8
9
6 1
5 2)
4 3
se cumple A = At
2.4 Transformaciones elementales por reglón. escalonamiento de una matriz. núcleo y
rango de una matriz.
Operaciones elementales de renglón para matrices
1. Intercambio de filas (Renglón): R i ←→ R j.
2. Cambio de escala: R i ←→ α R i (α ≠ 0).
3. Suma de filas: R i ←→ α R i + βR j (α ≠ 0).
Las cuales significan, respectivamente:
• La fila i se intercambia con la fila j.
• La fila i se cambia por la misma fila multiplicada por α.
• La fila i se cambia por la suma de α-veces la fila i con β-veces la fila j.
Escalonamiento de una matriz:
Definición 2.4.b La matriz A ∈ ℳ m×n está en forma escalonada si se cumplen las siguientes
dos condiciones. Donde ℳ m×n : son matrices genéricas de orden, m filas por n columnas.
• Las filas nulas (si existen)1 están por debajo de las filas no nulas.
• El primer elemento distinto de cero de cada fila no nula está a la derecha del primer
elemento diferente de cero de las filas precedentes.2
Ejemplo 2.4.b Si
0 −1
0 0
A= 0 0
0 0
[0 0
2 3 −5 3
−10 2 4
00 0 1
00 0 0
0 0 0 0]
y
−1
0
B= 0
0
[0
2 4
1 2
0 1
0 2
0 0
0
−3
0
−3
0
3
4
2
0
0]
A está en forma escalonada pero B no.
1 Una fila es nula si todas sus entradas son ceros; una fila es no nula si por lo menos una de
sus componentes es distinta de cero.
2 En el caso que el primer elemento distinto de cero esté en la primera fila, se sobreentiende
que la condición se cumple por vacuidad.
Definición 2.4.b.1 Al primer elemento distinto de cero de cada fila no nula, de una matriz en
forma escalonada, se le llama pivote.
Definición 2.4.b.2 Un sistema H 𝑥⃗ = 𝑐⃗ está escalonado si la matriz ampliada [ H | 𝑐⃗ ] es una
matriz escalonada. A las variables que correspondan a pivotes en un sistema escalonado se
les llamarán variables ligadas (o principales o básicas) y a las restantes variables libres (o
no básicas)
Ejemplo 1.24 En el sistema escalonado 4 × 6
𝟏
[(0
0
0
0 3−2 1
0 𝟓0 1
0 00 𝟕
0 00 0
5 −2
1| 3 )] ,
6 7
𝟓 0
hay pivotes en las columnas 1, 3, 5 y 6; que corresponden, respectivamente, a las variables
x1, x3, x5 y x6. Así que estas variables son ligadas y x2, x4 son variables libres.
Núcleo y rango de una matriz.
Definicion
Si A 𝑝𝑒𝑟𝑡𝑒𝑛𝑒𝑐𝑒 𝑎 𝑙𝑎𝑠 𝑚𝑎𝑡𝑟𝑖𝑐𝑒𝑠 𝑑𝑒 𝑚 𝑓𝑖𝑙𝑎𝑠 𝑦 𝑛 𝑐𝑜𝑙𝑢𝑚𝑛𝑎𝑠. ℳ mxn. se definen:
1. Rango fila de A: Rf (A) es igual a la dimensión del espacio de filas de A.
dim (Ef (A).
2. Rango columna de A: Rc (A) es igual a la dimensión del espacio de columnas
de A. dim (Ec (A).
3. Nulidad de A. nul(A). como la dimensión del espacio nulo de A.
Teorema Sean A ∈ ℳ m x n y H una forma escalonada equivalente, entonces:
1. El rango fila de A es el número de filas no nulas de H.
2. El rango columna de A es el número de columnas con pivote de H.
3. Rf (A) = Rc (A).
4. La nulidad de A es el número de columnas sin pivote de H.
Ejemplo Hallar:
1. Rf (A).
2. Rc (A).
3. Nul (A).
Si A es la matriz
1
1
2
3
[1
Solución
1
0
𝐴 → 0
0
[0
2
3
5
6
5
0
1
1
0
3
−1 1
1 −1
0 0
0 −6
5 −5]
llevando la matriz a forma escalonada
2
1
1
0
3
0
1
1
0
3
−1 1
2 −2
2 −2
3 −9
6 −6]
→
1
0
0
0
[0
2
1
0
0
0
0
1
0
0
0
−1 1
2 −2
1 −3
0 0
0 0]
1. Las filas distintas de cero de la forma escalonada, luego Rf (A) = 3, a saber
las filas 1, 2 y 3.
2. Las columnas de A correspondientes a columnas con pivote en la forma
escalonada y Rc(A) = 3. a saber las columnas 1, 2 y 4.
3. La solución al sistema homogéneo es:
x1
2
10
2𝑠 + 10𝑟
𝑥2
−1
−4
−𝑠 − 4𝑟
𝑠
𝑥3 =
=𝑟 0 +𝑠 1
3𝑟
𝑥4
3
0
[
]
[𝑥5]
[1]
[0]
𝑟
Entonces Nul (A) = 2. A saber las columnas 3 y 5.
Teorema
Si A ∈ ℳ m×n, entonces Rang(A) + Nul(A) = n.
Equivalentemente para el sistema A𝑥⃗ = ⃗0⃗:
1. Rang(A) = número de variables ligadas.
2. Nul(A) = número de variables libres.
3. Rang(A) + Nul(A) = n
Del ejemplo anterior
Rang(A) + Nul(A) = n
3
+ 2
=5
2.5 Cálculo de la inversa de una matriz.
Es conocido que:
5-1 * 5 = 1
y
5 * 5-1 = 1
luego de forma análoga en notación
matricial (del recíproco o inverso multiplicativo) de un número diferente de cero.
Se dice que una matriz A de n × n es invertible si existe otra matriz C de n × n tal que
CA = I y AC = I
donde I = 𝐼𝑛 , la matriz identidad n × n.
Este inverso único se denota mediante 𝐴−1 , de manera que,
A-1A = I y AA-1 = I
Una matriz que no es invertible algunas veces se denomina matriz singular, y una matriz
invertible se denomina matriz no singular.
La generalización matricial requiere ambas ecuaciones y evita la notación con diagonales
(para indicar una división) debido a que la multiplicación de matrices no es conmutativa.
Más aún, una generalización completa sólo es posible si las matrices involucradas son
cuadradas.
Teorema
𝑎
Sea 𝐴 = [
𝑐
𝑏
]. Si ad − bc ≠ 0, entonces A es invertible y
𝑑
1
𝐴−1 = (𝑎𝑑−𝑏𝑐) [
𝑑
−𝑐
−𝑏
]
𝑎
Si ad – bc = 0, entonces A no es invertible.
Ejemplo
1
hallar 𝐴−1 , si A = [
3
−2
] , entonces a d -b c = 1(0)-(-2)(3) = 0 + 6 = 6 ,
0
entonces A es invertible y:
−1
𝐴
0
0 2
= 6[
]=[ 1
−3 1
−2
1
1
3
1]
6
2.6 Definición de determinante de una matriz.
Se define el determinante de una matriz A = [a] de 1 x 1 como
det A = | a | = a
𝑎11
Recordando que la inversa de una matriz es: [𝑎
21
𝑎12 −1
𝑎22
1
]
=
[
𝑎22
𝑎11 ∗𝑎22 −𝑎12 ∗𝑎21 −𝑎21
−𝑎12
𝑎11 ]
donde
𝑎11 ∗ 𝑎22 − 𝑎12 ∗ 𝑎21 se le llama el determinante de A o det A. ó | A |
ADVERTENCIA: No confundir con el valor absoluto.
𝑎11
Definición. Sea 𝐴 = [𝑎21
𝑎31
𝑎22
det A = |A| = 𝑎11 ∗ |𝑎
32
𝑎12
𝑎22
𝑎32
𝑎13
𝑎23 ] . Entonces el determinante de A es el escalar
𝑎33
𝑎23
𝑎21
𝑎33 | − 𝑎12 ∗ |𝑎31
𝑎23
𝑎21
𝑎33 | + 𝑎13 ∗ |𝑎31
𝑎22
𝑎32 | (1)
entonces, se
puede abreviar como
𝑑𝑒𝑡𝐴 = 𝑎11 𝑑𝑒𝑡𝐴11 − 𝑎12 𝑑𝑒𝑡𝐴12 + 𝑎13 𝑑𝑒𝑡𝐴13
= ∑3𝑗=1(−1)1+𝑗 𝑎1 j 𝑑𝑒𝑡𝐴1 𝑗
Para cualquier matriz cuadrada A, det A i j se llama menor - (i, j) de A-.
Esto se extiende naturalmente a matrices cuadradas arbitrarias.
Definición 1: sea 𝐴 = [𝑎𝑖𝑗 ] una matriz de n x n, donde n ≥ 2. entonces el determinante de A
es el escalar
𝑑𝑒𝑡𝐴 = |𝐴| = 𝑎11 𝑑𝑒𝑡𝐴11 – 𝑎12 𝑑𝑒𝑡𝐴12 + ... + (−1)1+𝑛 𝑎1n 𝑑𝑒𝑡𝐴1𝑛
= ∑𝑛𝑗=1 (−1)1+𝑗 𝑎1j 𝑑𝑒𝑡𝐴1𝑗
es conveniente combinar un menor con su signo más o menos. Para este fin, se define el
cofactor - (i, j)- de A como
𝐶𝑖 𝑗 = (−1)î+𝑗 𝑑𝑒𝑡 𝐴𝑖 𝑗
con esta notación, la definición 1 se convierte en
𝑛
𝑑𝑒𝑡𝐴 = ∑ 𝑎1j 𝐶1j
𝑗=1
Teorema 2.6 Teorema de expansión de Laplace
El determinante de una matriz A de n x n, donde n ≥ 2, puede calcularse como
det A = a i1 C i1 +a i2 Ci2 + ... + a i n C i n
= ∑𝑛𝑗=1 𝑎𝑖 𝑗 𝐶𝑖 𝑗 que es la expansión por cofactores a lo largo del iésimo renglón y también como
𝑑𝑒𝑡𝐴 = 𝑎1𝑗 𝐶1j + 𝑎2𝑗 𝐶2j + ... + 𝑎𝑛𝑗 𝐶𝑛𝑗
= ∑𝑛𝑖=1 𝑎𝑖 𝑗 𝐶𝑖 𝑗 que es la expansión por cofactores a lo largo de la
j-ésima columna.
Teorema 2.6
El determinante de una matriz triangular es el producto de las entradas en su diagonal
principal.
Específicamente, si A = [a i j] es una matriz triangular de n x n, entonces
det A = a11 a22 ... a n n
1
a) si 𝐴 = (4
7
= 1|
2 3
5 6) cual es su determinante?
8 9
4 6
5 6
4 5
| −2|
| + 3|
| = 1[5(9)-6(8)]-2[4(9)-6(7)]+3[4(8)-5(7)]
7 9
8 9
7 8
= 1[45-48]-2 [36-42]+3 [32-35]
= -3+12-9 = 0
2.7 propiedades de los determinantes
Teorema 2.7
Sea 𝐴 = [𝑎𝑖 𝑗 ] una matriz cuadrada.
a. Si A tiene un renglón (columna) cero, entonces
det A = 0.
b. Si B se obtiene al intercambiar dos renglones (columnas) de A, entonces det B = - det A.
c. Si A tiene dos renglones (columnas) idénticos, entonces
det A = 0.
d. Si B se obtiene al multiplicar un renglón (columna) de A por k, entonces det B = k det A.
e. Si A, B y C son idénticas, excepto que el i-ésimo renglón (columna) de C es la suma de los
i-ésimos renglones (columnas) de A y B, entonces
det C = det A + det B.
f. Si B se obtiene al sumar un múltiplo de un renglón (columna) de A a otro renglón
(columna), entonces
det B = det A.
Ejemplos:
a.1
𝑎𝑏𝑐
0
0 0
si 𝐴 = (000) entonces |A| =𝑎 |
|−𝑏|
𝑔
ℎ 𝑖
𝑔ℎ𝑖
0
0
|+𝑐|
𝑖
𝑔
0
|
ℎ
= a[0(i)-0(h)]-b[0(i)-0(g)]+c[0(h)-0(g)] = 0
b.1
7
si𝐴 = (4
1
8 9
5 6) si c1 ↔ c2
2 3
4
luego |B| = 8 |
1
5
Entonces |A| = 7 |
2
8 7
entonces𝐵 = (5 4
2 1
9
6)
3
6
5 6
5 4
| − 7|
| +9|
| = 8[12-6] -7[15-12]+9[5-8] = 48 -21-27 = 0
3
2 3
2 1
4
6
| − 8|
1
3
6
4 5
| + 9|
| = 7[15-12]-8[12-6]+9[8-5] = 21-48+27 = 0
3
1 2
por tanto |B| = - |A|
c.1
7
𝐶 = (7
1
8 9
8
8 9) entonces |C| = 7 |
2
2 3
9
7 9
7 8
| − 8|
| +9|
| = 7(24-18) -8(21-9) +9(143
1 3
1 2
8)
= 42 - 96 + 54 = 0
por lo que se cumple |C| = 0 cuando las filas 1 y 2 se repiten.
d.1
si 𝐴 = [
1 2
1
] y k = 5. entonces R1↔k*R1, luego |B| = R1↔5* R1 =5 |
3 4
3
2
5 10
|=|
|y
4
3 4
= (20-30) = -10
e.1
1 2 3
1 2
si 𝐴 = 𝐵 = [3 4 5] y 𝐶 = [3 4
5 6 7
4 6
3
5]
8
entonces |C| = |A| + |B|
4
1|
6
3
3|
5
5
3
| − 2|
8
4
4
|
6
3
5
| + 3|
4
8
por lo que
4
3 4
4 5
3 5
4
|= 1|
| − 2|
| + 3|
| +1 |
6
5 6
6 7
5 7
6
5
3
| − 2|
7
5
5
|+
7
1(32-30)-2(24-20) +3(18-16) = [1(28-30)-2(21-25) +3(18-20)] + [1(28-30)-2(21-25) +3(1820)]
2-8+6 = [-2+8-6] + [-2+8-6]
0
=
0
+
0
0 = 0 por lo cual queda demostrada la propiedad
f.1
si
1
𝐴 = [3
5
2 3
4 5] entonces
6 7
1
R 1 ↔ 3 + R 1 [3
5
luego
2 3
4 5]
6 7
4 5 6
𝐵 = [3 4 5 ]
5 6 7
|B|=|A|
desarrollando
4 5
3
4|
| − 5|
6 7
5
3
5
| + 6|
5
7
4
3 4
4 5
3 5
| = 1|
| − 2|
| + 3|
|
6
5 6
6 7
5 7
[4(28-30)-5(21-25) +6(18-20)]
[-8+20-12]
0
= [1(28-30)-2(21-25) +3(18-20)]
= [-2+8-6]
=
0
por lo que queda demostrada la propiedad.
2.8 Inversa de una matriz cuadrada a través de la adjunta.
Definición. Sea A una matriz cuadrada de orden n. Se definen:
• La matriz de cofactores de A como Cof (A) = [ c i j], donde c i j es el cofactor del elemento i
j de A.
• La matriz adjunta de A por Adj (A) = [ Cof (A)] t; es decir, la matriz adjunta de A es la
transpuesta de la matriz de cofactores.
Teorema (Método de la adjunta) Si A ∈ ℳ n x n, entonces
𝐴 𝐴𝑑𝑗(𝐴) = 𝑑𝑒𝑡(𝐴)𝐼𝑛.
𝑎11
𝑎21
⋮
= 𝑎𝑖1
⋮
[𝑎𝑛1
𝑎12
𝑎22
⋮
𝑎𝑖2
⋮
𝑎𝑛2
… 𝑎1𝑛
… 𝑎2𝑛
⋱ ⋮
… 𝑎𝑖𝑛
⋱
⋮
… 𝑎𝑛𝑛]
𝑐11
𝑐12
[
⋮
𝑐1𝑛
… 𝑐𝑗1 …
… 𝑐𝑗2 …
⋮
⋮
𝑐2𝑛 … 𝑐𝑗𝑛 …
𝑐𝑛1
𝑐𝑛2
𝑐21
𝑐22
⋮
]
𝑐𝑛𝑛
El elemento en el i-ésimo renglón y la j-ésima columna de este producto es
ai1 Cj1 + ai2 Cj2 +… + ain Cjn.
Si i = j, entonces la suma es simplemente la expansión por cofactores de A a lo largo de su iésimo renglón, lo que significa que la suma es el determinante de A. Por otra parte, si i ≠ j,
entonces la suma es cero.
det(𝐴)
A[Adj(A)] = [ 0
⋮
0
0 … 0
det(𝐴) … 0
] = det(A)I
⋮ ⋱ ⋮
0 … det(𝐴)
Luego, A es invertible si y sólo si det (A) ≠ 0 y en tal caso
1
det(𝐴)
1
A[Adj(A)] = I o A [det(𝐴) 𝐴𝑑𝑗(𝐴)] = 𝐼.
Se sigue que
1
𝐴−1 = | 𝐴 | 𝐴𝑑𝑗(𝐴).
Ejemplo
−1
Hallar A-1, donde A = [ 0
1
3 2
−2 1 ]
0 −2
SOLUCIÓN
Desarrollando por la columna 1
Det A = -1((-2)(-2)-0) + 1(3+4) = -1(4-0) +1(7) = -1(4) +7= 3
−2 1
C11 = (-1)2[
]= 4;
0 −2
0 −2
C13 = (-1)4[
] = 1(2) = 2
1 −0
C12 = (-1)3[
C21 = (-1)3[
3 2
] = -1(-6) = 6;
0 −2
−1 3
C23 = (-1)5[
] = - 1(-3)= 3
1 0
C22 = (-1)4[
3 2
] = 1(3+4)= 7;
−2 1
−1 3
C33 = (-1)6[
] = 1(2 − 0) = 2
0 −2
C32 =(-1)5[
C31 = (-1)4[
0 1
]= -1 (– 1) = 1;
1 −2
−1 2
] = 1(2-2)=0 ;
1 −2
−1 2
] = -1(-1-0)= 1;
0 1
4
−1
𝐴
1
= | 𝐴 | 𝐴𝑑𝑗(𝐴) =
1
3
4
[1
2
6 7
0 1] =
3 2
3
1
3
2
2
0
[3 1
7
3
1
3
2
3]
2.9 Aplicación de matrices y determinantes.
Aplicación de matrices
Del Premio Nobel Wassily Leontief, el modelo económico descrito es la base de
modelos más complejos usados actualmente en muchas partes del mundo.
Suponga que la economía de una nación se divide en n sectores que producen bienes o
servicios, y sea X un vector de producción en ℝn que enlista lo producido por cada sector en
un año. También, suponga que otra parte de la economía (llamada sector abierto) no produce
bienes ni servicios, sino que solamente los consume, y sea D un vector de demanda final (o
relación de demandas finales) que enlista los valores de los bienes y servicios demandados a
los diversos sectores por la parte no productiva de la economía. El vector “d” puede
representar la demanda del consumidor, el consumo del gobierno, la producción sobrante, las
exportaciones, u otras demandas externas.
Conforme los diversos sectores producen bienes para satisfacer la demanda del
consumidor, los productores crean por sí mismos una demanda intermedia adicional de
bienes que necesitan como insumos para su propia producción. Las interrelaciones de los
sectores son muy complejas, y la conexión entre la demanda final y la producción no es clara.
Leontief se preguntó si hay un nivel de producción x tal que las cantidades producidas (o
“suministradas”) equilibren exactamente la demanda total de esa producción, de modo que
𝑐𝑎𝑛𝑡𝑖𝑑𝑎𝑑
𝑑𝑒𝑚𝑎𝑛𝑑𝑎
𝑑𝑒𝑚𝑎𝑛𝑑𝑎
{𝑝𝑟𝑜𝑑𝑢𝑐𝑖𝑑𝑎} = {
} + { 𝑓𝑖𝑛𝑎𝑙 } ........(1)
𝑖𝑛𝑡𝑒𝑟𝑚𝑒𝑑𝑖𝑎
𝑋
𝐷
Ejemplo:
Suponer que la economía (abierta) consiste en tres sectores: manufactura, agricultura y
servicios. con los vectores unitarios de consumo C1, C2, C3 mostrados en la tabla siguiente:
Insumos consumidos
por unidad
de producción
Comprado por :
Manufactura
Agricultura
Servicios
Manufactura
.50
.40
.20
Agricultura
.20
.30
.10
Servicios
.10
.10
.30
↑
↑
↑
C1
C2
C3
La demanda intermedia total de los tres sectores está dada por {demanda intermedia}
= X1C1 + X2 C2 + X3 C3
= CX
donde C es la matriz de consumo [ C1
.50 .40
𝐶 = [.20 .30
.10 .10
C2
......(2)
C3], a saber,
.20
.10] ..........(3)
.30
Las ecuaciones (1) y (2) producen el modelo de Leontief.
EL MODELO DE LEONTIEF DE ENTRADA-SALIDA, O ECUACIÓN DE PRODUCCIÓN
X
=
CX
+
D
Cantidad
Demanda
Demanda
producida
intermedia
final
...... (4)
Si se escribe X como IX y se utiliza álgebra de matrices, es posible reescribir (4):
IX − CX
=D
(I − C) X
=D
....... (5)
a)
Considere la economía cuya matriz de consumo está dada por (3). Suponga que la demanda
final es de 50 unidades para manufactura, 30 unidades para agricultura, y 20 unidades para
servicios. Encuentre el nivel de producción X que satisfará esta demanda.
La matriz de coeficientes en (5) es
1
𝐼– 𝐶 = [0
0
0 0
.5 .4 .2
.5 −.4 −.2
1 0] − [.2 .3 .1] = [−.2 .7 −.1]
0 1
.1 .1 .3
−.1 −.1 .7
Para resolver (5), reducir por filas la matriz aumentada
.5 −.4 −.2 50
5 −4 −2
[−.2 .7 −.1 30] ~ *10 = [−2 7 −1
−.1 −.1 .7 20
−1 −1 7
500
300] ~ ... ~
200
1
[0
0
0 0
1 0
0 1
226
119]
78
La última columna se redondea a la unidad más cercana.
El
área
de
manufactura
debe
producir
aproximadamente
226
unidades, agricultura 119 unidades, y servicios únicamente 78
unidades.
b) Aplicación de determinantes
TEOREMA
Si A es una matriz de 2 × 2, el área del paralelogramo determinado por las columnas de A es
|det A|. Si A es una matriz de 3 × 3, el volumen del paralelepípedo es determinado mediante
las columnas de A es |det A|. pudiendo ser área donde un vector de ellos es cero.
0
[ ]
4
7
[ ]
0
Area = | 7 ‧ 4 |
|𝑑𝑒𝑡 [
7 0
]| = |7 (4)| = 28 : {área del rectángulo}
0 4
Sean 𝑎1 y 𝑎2 vectores diferentes de cero. Entonces, para cualquier escalar C, el área del
paralelogramo determinado mediante 𝑎1 y 𝑎2 es igual al área del paralelogramo determinado
por 𝑎1 y 𝑎2 dado en unidades de superficie o unidades de área.
Para obtener el volumen de un paralelepípedo, teniendo en cuenta, los vectores columna
3 0 0
[0] [2] [0]
0 0 1
3 0 0
Volumen = | a b c |. |𝑑𝑒𝑡 [0 2 0]| = | 3 (2) 1 | = 6 u. v.
0 0 1
o unidades volumétricas.
Dos paralelogramos de igual área
2
6
c) Calcule el área del paralelogramo determinado por los vectores columna [ ] y [ ]
5
1
2 6
𝐴=[
] |det A| = |2(1)-6(5)| = |2-30| = |-28| ,
5 1
el área del paralelogramo es 28 unidades de superficie
2
[ ]
5
6
[ ]
1
o 28 unidades de área.