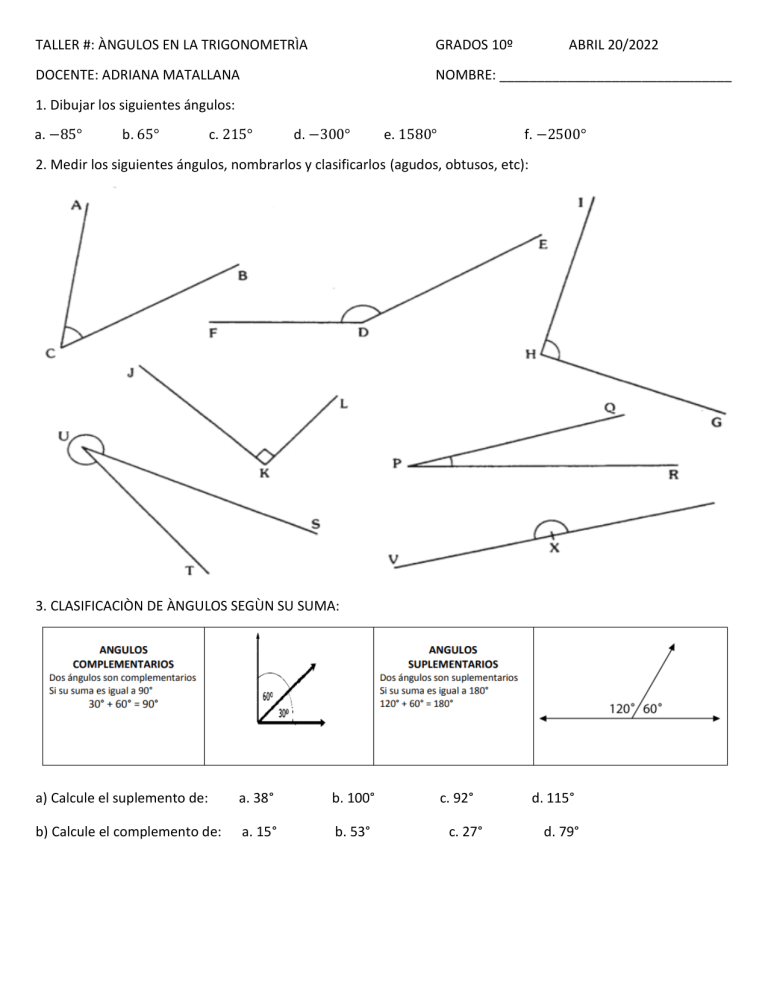
TALLER #: ÀNGULOS EN LA TRIGONOMETRÌA GRADOS 10º ABRIL 20/2022 DOCENTE: ADRIANA MATALLANA NOMBRE: _______________________________ 1. Dibujar los siguientes ángulos: a. −85° b. 65° c. 215° d. −300° e. 1580° f. −2500° 2. Medir los siguientes ángulos, nombrarlos y clasificarlos (agudos, obtusos, etc): 3. CLASIFICACIÒN DE ÀNGULOS SEGÙN SU SUMA: a) Calcule el suplemento de: a. 38° b. 100° b) Calcule el complemento de: a. 15° b. 53° c. 92° c. 27° d. 115° d. 79° 4. CLASIFICACIÒN DE ÁNGULOS SEGÚN SU POSICIÒN Sus medidas suman 180 grados Calcular el valor de x en cada caso: 5. ANGULOS EN POSICIÒN NORMAL: Un ángulo está en posición normal si su vèrtice coincide con el origen del plano cartesiano y su lado inicial coincide con el eje X positivo, asì: ANGULOS COTERMINALES: Son aquellos ángulos en posición normal con diferente medida cuyo lados final e inicial coinciden. En la gráfica anterior, los ángulos (a) y (c) son coterminales. Para hallar ángulos positivos que sean coterminales con un ángulo ϴ, sumamos cualquier múltiplo de 360º, ejemplo: 30° + 360° = 390° 𝑦 30° + 720° = 750° Son coterminales con 𝛳 = 30°. Para hallar ángulos negativos que sean coterminales con ϴ, restamos cualquier mùltiplo de 360°. Asì: 30° − 360° = −330° 𝑦 30 − 720° = −690° son coterminales con 𝛳. Encontrar dos ángulos coterminales positivos y dos negativos para cada ángulo: a) 45° b) -85° c) 100° d) 570 e) -150° 6. Recordemos que: DE DECIMAL A SEXADESIMAL: DE SEXAGESIMAL A DECIMAL: 18,72° = i. Exprese en grados minutos y segundos los siguientes ángulos a. 245,276° b. 45,48° g. 18,42° h. 215, 7° c. −156,62° d. 357,892° e. 150,63° f. −31,86° ii. Exprese en grados los siguientes ángulos. a. 100° 20′ 53′′ b. 240° 15′ 36′′ e. −47° 26`38`` f. 59’ 16’’ c. 56° 46′ 74′′ d. 67° 35′ 59′′ 7. Sumas y restas de ángulos en sistema sexadecimal: Suma: Resta: Multiplicaciòn: Realizar las siguientes operaciones: a. 12° 43’ 30” + 13° 23’ 42” b. 53’ 34” + 12’ 22” c. 4° 23’ 40” − 1° 16’ 32” d. 12° 27’ 55” − 7° 15’ 54” e) 60° 23’ 59’’ × 3 f. 20°44’ 11’’ × 4 8. Recuerda, para expresar un ángulo de radianes a grados, se multiplica 180 2𝜋 𝜋 ∙𝜃 Ejemplo: Expresar 𝑟𝑎𝑑 en grados: 9 180 2𝜋 × 𝜋 9 180(2𝜋) 2𝜋 = 𝜋(9) Luego, 9 360 = 9 = 40° Ahora, para expresar de grados a radianes, se multiplica = 40° 𝜋 180 ∙ 𝜃 𝑟𝑎𝑑 . Ejemplo: Expresar 120° a radianes: 𝜋 120 × 180 120𝜋 = 180 Luego, 120° 2𝜋 = 3 = 2𝜋 3 𝑟𝑎𝑑 i) Expresar en radianes los siguientes ángulos: a) 15º f) 90º b) 35º g) −60º c) 80º h) 45º d) −150º i) 30º e) 200º j) 330º ii) Expresar en grados los siguientes ángulos: 9. En papel milimetrado, construir la siguiente circunferencia, una con las medidas en grados y otra con las medidas en radianes (ojo, usar el transportador para que queden bien medidos). La circunferencia puede tener cualquier radio: