Trigonometría
Anuncio
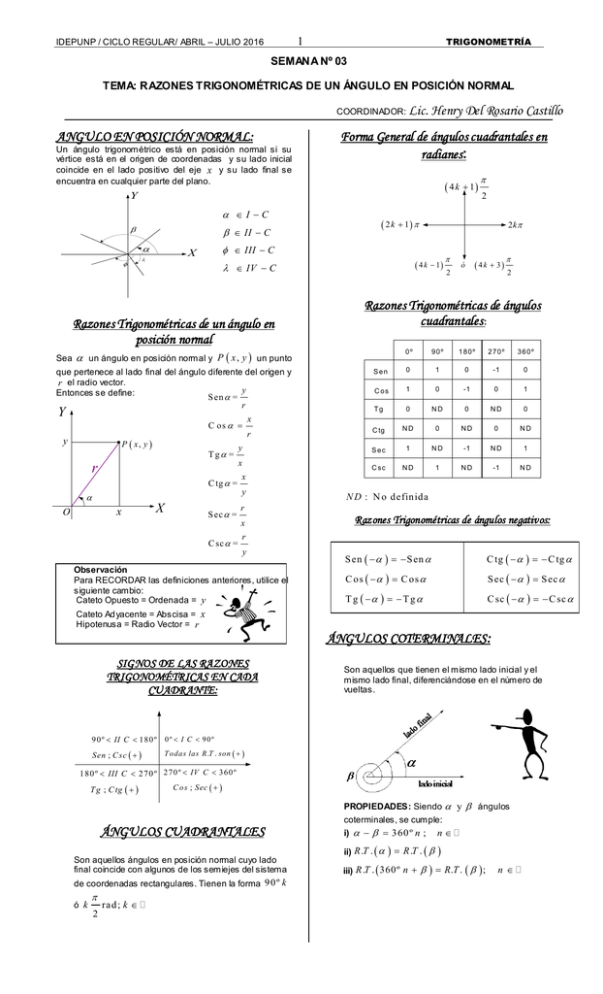
TRIGONOMETRÍA 1 IDEPUNP / CICLO REGULAR/ ABRIL – JULIO 2016 SEMANA Nº 03 TEMA: RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL COORDINADOR: Lic. ANGULO EN POSICIÓN NORMAL: Un ángulo trigonométrico está en posición normal si su vértice está en el origen de coordenadas y su lado inicial coincide en el lado positivo del eje x y su lado final se encuentra en cualquier parte del plano. Henry Del Rosario Castillo Forma General de ángulos cuadrantales en radianes: 4 k 1 Y I C II C Sea que pertenece al lado final del ángulo diferente del origen y r el radio vector. y Entonces se define: S en = r Y C os T g = y x r C tg = x O X S ec = 2 0º 90º 180º 270º 360º Sen 0 1 0 -1 0 C os 1 0 -1 0 1 Tg 0 ND 0 ND 0 C tg ND 0 ND 0 ND Sec 1 ND -1 ND 1 C sc ND 1 ND -1 ND N D : N o d efin id a r x C sc = 4k 3 x y ó 2 x r P x, y Razones Trigonométricas de ángulos cuadrantales : un ángulo en posición normal y P x , y un punto y 2k 4 k 1 IV C Razones Trigonométricas de un ángulo en posición normal 2 2 k 1 III C X Razones Trigonométricas de ángulos negativos: r y Observación Para RECORDAR las definiciones anteriores, utilice el siguiente cambio: Cateto Opuesto = Ordenada = y S en S en C tg C tg C os C os S ec S ec T g T g C sc C sc Cateto Ad yacente = Abscisa = x Hipotenusa = Radio Vector = r ÁNGULOS COTERMINALES : SIGNOS DE LAS RAZONES TRIGONOMÉTRICAS EN CADA CUADRANTE: 90 º II C 180 º 0º I C 90º Sen ; C sc T o da s la s R .T . son Son aquellos que tienen el mismo lado inicial y el mismo lado final, diferenciándose en el número de vueltas. 1 8 0 º III C 2 7 0 º 270 º IV C 360 º T g ; C tg C os ; Sec ÁNGULOS CUADRANTALES Son aquellos ángulos en posición normal cuyo lado final coincide con algunos de los semiejes del sistema de coordenadas rectangulares. Tienen la forma 9 0 º k ó k 2 rad ; k PROPIEDADES: Siendo y ángulos coterminales, se cumple: i) 360 º n ; n ii) R .T . R .T . iii) R .T . 360º n R.T . ; n