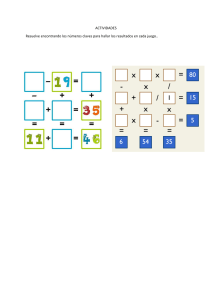
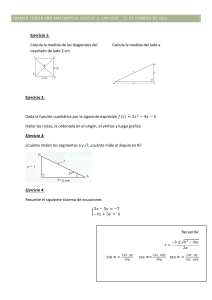
Práctica de Geometría: Segmentos y Ángulos - Ejercicios
Anuncio

SEMINARIO DE GEOMETRÍA (PRÁCTICA)-ADEC BAGUA 11) A, B, C y D son puntos colineales y consecutivos tal que AB + AD = 64. Si C es punto medio de BD. Hallar AC. A) 32 B) 30 C) 28 D) 24 E)27 Docente: Bach. Leonardo Bazán Vásquez. 12) Sea los puntos colineales y consecutivos A, B, C y D. Si AB = 8, CD = 9. Hallar BC, si: AC.CD + AB.BD = BC.AD. A) 8 B) 9 C) 12 D) 18 E) 20 SEGMENTOS. EJERCICIOS. ⃐ 1) Si “M” es punto medio del 𝐀𝐁 , calcula “x”. A) 13 u E)11 u B) 6 u C) 10 u 13) P, Q y R son puntos colineales y consecutivos, tales que 2PQ + 3QR = 83 Hallar QR, si PR = 36 A) 9 B)11 C)12 D) 14 E) 17 D) 14 u ÁNGULOS EJERCICIOS. 2) En una recta se ubican los puntos colineales A, B, C y D. Si AB = 4a, BC = 4 cm y CD = 2a y además AD = 30 cm, calcula la distancia entre los puntos medios de AB y CD. A) 17 B) 7 C) 19 D) 14 E)13 3) Sean los puntos colineales y consecutivos A, B, C y D tal que: BC=AB+1 y CD=AB-3. Calcule AD, si AB es mínimo entero. A) 1 B) 9 C) 10 D) 12 E)13 4)Sobre una línea recta se consideran los puntos colineales y consecutivos A, B y C tal que: 𝐀𝐁 𝟐 = y 𝐁𝐂 𝟑 2AB+3BC = AC+96. Halle AB. A) 12 B) 24 C) 16 E) 48 D) 20 5) En una recta se ubican los puntos colineales A, B, C, D y E, tal que B y C, son puntos medios de ⃐𝐀𝐃 y ⃐𝐁𝐄 respectivamente. Si CD=2 m y numéricamente: 𝟏 𝑩𝑬 - 𝟏 𝐀𝐃 A) 25 E) 18 = 𝟏 𝟖𝟎 . B) 20 C) 16 D) 30 6) En una recta se ubican los puntos consecutivos A, O, B, C y D. Si AC= 2AO: 𝟏 𝑨𝑩 OB∙OD=144.Halla AO en metros. A) 6 m B) 8 m C) 10 m E) 14m + 𝟏 𝐀𝐃 = 𝟐 𝑨𝑪 y D) 12 m 7) Los puntos colineales y consecutivos A, B y C. Si AB = 2BC + 1 y AC = 49. Hallar BC. A) 12 B) 15 C) 16 D) 18 E)22 8) Los puntos colineales y consecutivos A, B, C y D. Son tales que: AD = 23, BD = 14 y AC = 15 Hallar: BC. A)5 B)6 C)7 D) 8 E)11 9) A, B y C son puntos colineales y consecutivos, tales que 7AB = 8BC y AC = 75. Hallar BC. A) 24 B) 35 C) 28 D) 27 E)29. 10) Los puntos consecutivos M, N, P y Q pertenecen a la misma recta. N es punto medio de MQ. Hallar NP, si MP – PQ = 48 A) 12 B) 16 C) 20 D) 24 E) 25 6. 7. 5. Calcular “x”: 8. A) 55° B) 65° C) 70° D) 90° E) 80° 6. Calcula “x”, si AB = BC = BD A) 55° B) 35° C) 30° D) 45° E) 65° 7. Calcula “x”, si AB = BC y CD = DE, A) 25° B) 15° C) 20° D) 30° E) 45° 11. 8. Calcula “x”, si BD es bisectriz del ∠ABC. A) 15° B) 12° C) 17° D) 20° E) 25° 12. TRIÁNGULOS EJERCICIOS. Si en un triángulo rectángulo, un ángulo externo mide 140°, ¿cuál es la medida del ángulo externo del otro ángulo agudo? A) 20° B) 25° C) 40° D) 50° E) 70° 1. 11. Calcula “ϴ”, si: AB = BD y m∠CAE = m∠ABD = m∠ACB. A) 50° B) 60° C) 80° D) 55° E) 70° 𝒙 2. Calcular “ ”: 𝒚 A) 0.50 B) 1.50 C) 1.00 D) 2.00 E) 3.00 3. Calcular “x”: A) 50° B) 150° C) 100° D) 200° E) 110° 4. Calcular “x”: A) 15° B) 25° C) 30° D) 40° E) 50° 12. Calcula “x”. A) 37.5° B) 40° C) 39° D) 30° E) 20° 13. Calcula “α”. A) 25° B) 24° C) 15° D) 10° E) 20° «Si he logrado ver más lejos, ha sido porque he subido a hombros de gigantes» Isaac Newton