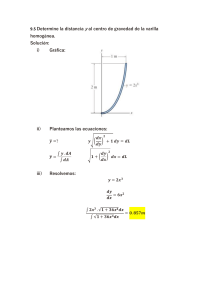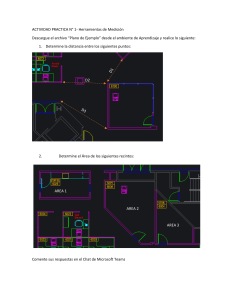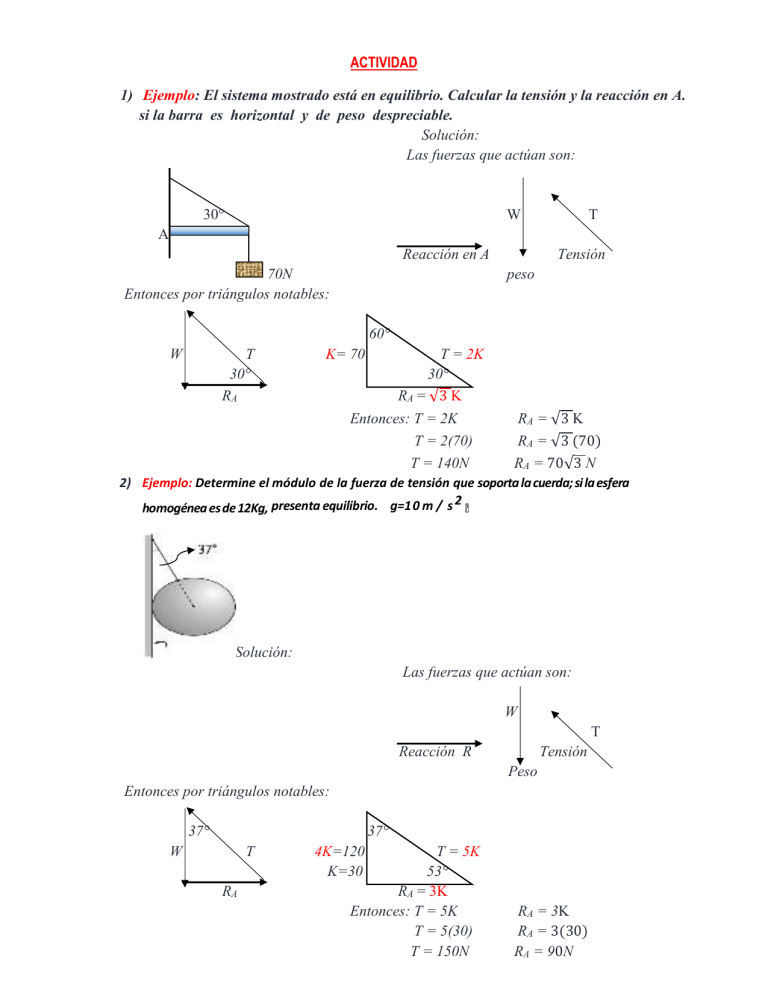
ACTIVIDAD 1) Ejemplo: El sistema mostrado está en equilibrio. Calcular la tensión y la reacción en A. si la barra es horizontal y de peso despreciable. Solución: Las fuerzas que actúan son: 30° W T A Reacción en A 70N Entonces por triángulos notables: Tensión peso 60° W T 30° RA K= 70 T = 2K 30° RA = √3 K Entonces: T = 2K T = 2(70) T = 140N RA = √3 K RA = √3 70 RA = 70√3 N 2) Ejemplo: Determine el módulo de la fuerza de tensión que soporta la cuerda; si la esfera 2 homogénea es de 12Kg, presenta equilibrio. g=1 0 m / s 37° Solución: Las fuerzas que actúan son: W T Reacción R Tensión Peso Entonces por triángulos notables: 37° 37° W T RA 4K=120 K=30 T = 5K 53° RA = 3K Entonces: T = 5K T = 5(30) T = 150N RA = 3K RA = 3 30 RA = 90N 3) El sistema mostrado está en equilibrio. Calcular la tensión y la reacción en A. si la barra es horizontal y de peso despreciable. 60° A 100N 4) Determine el módulo de la fuerza de tensión que soporta la cuerda; si la esfera homogénea es de 80 2 N, presenta equilibrio. g=1 0 m / s 37° 5) Determine la fuerza que aplica la persona, sabiendo que el bloque de 800 N se encuentra equilibrado. (Las poleas son de masa despreciable y lisas). a) 400N b) 500N c) 600N d) 200N e) 300N