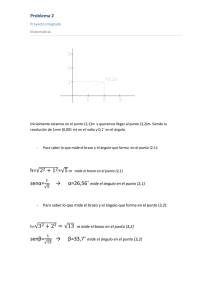
Cuando se trabaja en la creación de un plotter se tiene que analizar de manera detallada el como del movimiento del mismo, y es que en la programación del Arduino es necesario especificar los algoritmos que el brazo seguirá para dar paso a una ilustración, específicamente calcular los movimientos exactos que este tendrá que hacer según las coordenadas que se le otorguen. Para hallar dichos movimientos se tendrá en cuenta los ángulos que se formaran entre la base del plotter y cada una de sus extremidades, a través, de las siguientes ecuaciones: 𝑋 = 𝐼1 ∗ Cos(𝐴) + 𝐼2 ∗ 𝐶𝑜𝑠(𝐴 + 𝐵) 𝑌 = 𝐼1 ∗ 𝑆𝑖𝑛(𝐴) + 𝐼2 ∗ 𝑆𝑖𝑛(𝐴 + 𝐵) En donde “X” representa la distancia horizontal que hay desde la base a la punta del brazo, “Y” representa la distancia vertical que hay desde la base a la punta del brazo, “I1” representa la medida que tiene la extremidad mas cercana a la base del plotter, “I2” representa la medida que tiene la extremidad más alejada a la base del plotter, ”A” representa el valor del ángulo que existe entre el eje X y la extremidad más cercana a la base del plotter y “B” que representa el valor del ángulo que existe entre el eje X y la extremidad más alejada a la base del plotter. Se puede deducir que las ecuaciones cumplen la función de dar las coordenadas de un punto según los ángulos de las extremidades, ya que lo que se debe saber es lo contrario, se usara una maniobra típica de la robótica, que es, la cinemática inversa la cual se usara para hallar, luego de cambiar el sentido de las ecuaciones dadas, los ángulos requeridos. Lo primero que se hará es trazar una línea imaginaria en el plano que valla desde la base del plotter hasta la punta del brazo y, según el teorema de Pitágoras, el cual establece que “en todo triángulo rectángulo, la longitud de la hipotenusa es igual a la raíz cuadrada de la suma del área de las respectivas longitudes de los catetos” , tendrá una medida 𝑃 = √𝑋 2 + 𝑌 2 Esta línea imaginaria creara un triangulo entre las extremidades y el centro, lo que dará paso a la ley del coseno, la cual establece que “c 2 = a 2 + b 2 – 2 ab cos C “ y lo que establece una nueva ecuación: 𝑃 = 𝐼12 + 𝐼22 + 2 ∗ 𝐼2 ∗ 𝐼1 ∗ 𝐶𝑜𝑠(𝐵) Y que cambiando su sentido daría: 𝐶𝑜𝑠(𝐵) = 𝑃 − 𝐼12 − 𝐼22 2 ∗ 𝐼1 ∗ 𝐼2 Gracias a esta expresión y a la siguiente identidad trigonométrica: 𝑆𝑖𝑛( . ) = ±√(1 − 𝐶𝑜𝑠 2 ( . )) , se podrá hallar también el seno de e ángulo (B), siendo este 𝑆𝑖𝑛( 𝐵 ) = ±√(1 − 𝐶𝑜𝑠 2 (𝐵)) Ya con estos datos, se puede hacer la siguiente igualdad 𝑆𝑒𝑛(𝐵) 𝑇𝑎𝑛(𝐵) = 𝐶𝑜𝑠(𝐵) O 𝑇𝑎𝑛(𝐵) = ±√(1−𝐶𝑜𝑠(𝐵)) 𝐶𝑜𝑠(𝐵) Ya por último paso se despeja la “B” ±√1 − 𝐶𝑜𝑠(𝐵) 𝐵 = 𝐴𝑟𝑐𝑇𝑎𝑛(2 ∗ ( ) 𝐶𝑜𝑠(𝐵) Ya teniendo el valor del ángulo B solo quedaría hallar el ángulo A, el cual tiene un método de solución mucho mas simple. Este ángulo comparte la misma esquina que el triangulo cuadrado que se forma con la línea imaginaria que anteriormente se trazo y los paralelos de los ejes X y Y que intersecan en la coordenada establecida, lo que se debe hacer es tomar el ángulo de dicho triangulo (γ)y del triángulo que se formó en búsqueda del ángulo B, en la esquina que interseca con la base (β), y restarlos, esa será el valor del ángulo en A y al final dando como resultado la siguiente cinemática inversa: ±√1 − 𝐶𝑜𝑠(𝐵) 𝑓(𝑥) = (γ − β) , 𝐴𝑟𝑐𝑇𝑎𝑛(2 ∗ ( ) 𝐶𝑜𝑠(𝐵) En donde la primera parte se refiere el ángulo A y la segunda al ángulo B