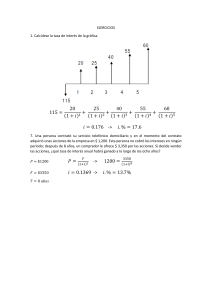
APUNTES ING. ECONOMICA 2021 PROBLEMAS UNIDAD 2 ING. ECONOMICA. Valor Anual 1. Compare las siguientes alternativas sobre la base de un valor anual, a una tasa de interés anual de 18%. Proyecto A Proyecto B Costo inicial, $ -250,000 -110,000 Costo anual de operación, $/año -130,000 -65,000 Ingresos anuales, $/año 400,000 270,000 Valor de salvamento, $ 50,000 20,000 Vida, años 6 4 VAA= [400000 + 50000(A/F,18%,6)] – [130000 + 250000 (A/P,18%,6) VAA= 405295.5 – 201477.5 =203818 ES RENTABLE VAB= [270000 + 20000(A/F, 18%,4)] –[65000 + 110000(A/P,18%,4)] VAB= 273834.8 – 105891.4 = 167943.4 ES RENTABLE AMBOS PROYECTOS SON RENTABLES 2. Se tienen las siguientes tres alternativas. Suponiendo una TMAR=20%, determine la mejor alternativa, usando el costo anual uniforme equivalente (CAUE). ALTERNATIVA 1 ALTERNATIVA 2 ALTERNATIVA 3 Inversión inicial $500 $600 $400 Vida útil 4 4 4 Valor de rescate 0 0 $20 Costo anual $80 $70 $100 CAUE= [80 + 500 (A/P,20%,4)] – [0] = CAUE= 80 + 500 * 0.38629 CAUE= 273.145 Costo anual CAUE= [70 + 600 (A/P,20%,4)] – [0] = CAUE= 70 + 600 * 0.38629 CAUE= 301.774 Costo anual CAUE= [100 + 400 (A/P,20%,4)] – [20(A/F,20%,4)] = CAUE= 100 + 400 * 0.38629 – 20 * 0.18629 CAUE= 250.79 Costo anual SE SELECCIONA LA ALTERNATIVA 3 POR TENER MENOR COSTO ANUAL UNIFORME 3. Compare las alternativas de la tabla de abajo sobre la base de un análisis de valor anual, aplicando una tasa de interés de 16% anual. Alternativa X Y Z Costo inicial, $ -150,000 -240,000 -310,000 Costo de operación en el -80,000 -60,000 -48,000 año 1, $ Incremento en el costo de operación cada año, $/año Valor de salvamento, $ Vida, años -3,000 -2,500 -1,000 20,000 3 32,000 4 36,000 6 X= [80000 + 3000 (A/G, 16%, 3) + 150000 (A/P, 16%,3)] – [20000(A/F, 16%,3)] = [80000 + 3000 (0.9014) + 150000 (0.44526)] – [20000(0.28526)] CAUE X = 144, 388 Y= [60000 + 2500 (A/G, 16%, 4) + 240000 (A/P, 16%,4)] – [32000(A/F, 16%,4)] Y= [60000 + 2500 (1.3156) + 240000 (0.35738)] – [32000(0.19738)] CAUE Y = 142,744.04 z= [48000 + 1000 (A/G, 16%, 6) + 310000 (A/P, 16%,6)] – [36000(A/F, 16%,6)] z= [48000 + 1000 (2.0729) + 310000 (0.27139)] – [36000(0.11139)] CAUE Z = 130,193.76 SE SELECCIONA LA ALTERNATIVA Z DEBIDO A QUE TENGA MENOR CAUE 4. Una compañía de mantenimiento industrial tiene dos alternativas para realizar los trabajos de pintura: manual y automático. En la tabla se presentan los datos de las alternativas. Manual Automático Inversión $0 $100,000 Capacitación (en año 0) $300 $100 Prestaciones sociales/hombre $3,000/año $1.200/año Seguro contra accidentes/hombre $1,000/año $4,350/año Mano de obra $4,200/año $4,200/año Número de trabajadores 6 2 Si se está planeando para un periodo de cuatro años y la TMAR=6%, ¿qué alternativa debe seleccionarse? Utilice el método de CAUE. Manual = [300(A/P, 6%, 6) + 3000 + 1000+ 4200] Manual = 8261.008 Automático = 100000(A/P, 6%, 2) – [100(A/P, 6%, 2) + 1200 + 4350 + 4200] Automático = 54544 – 9804.544 = 44739.456 Se selecciona la alternativa manual debido a que se tiene menor CAUE 5. Una compañía hotelera está considerando la posibilidad de construir un nuevo hotel en la Isla del Padre. El costo inicial de este hotel de 200 cuartos se estima en $100,000,000 y la amueblada, la cual es conveniente realizar cada cinco años se estima en $10,000,000. Los costos anuales de operación se estima que serían del orden de $20,000,000, y la tarifa diaria que se piensa cobrar es de $800. Por otra parte, esta compañía utiliza un horizonte de planeación de 10 años para evaluar sus proyectos de inversión. Por consiguiente, para este problema en particular la compañía estima que el valor de rescate del hotel después de 10 años de uso es de $10,000,000 y el valor de rescate de los muebles después de 5 años de uso es prácticamente nulo. Utilizando una TREMA del 20% anual y 365 días de operación al año, determine por el método del valor anual si conviene construir el hotel suponiendo una ocupación diaria del: a) 50% INGRESOS= 800*365*100= 29,200,000 CAUE= [29,200,000 + 100,000,000 (A/F, 20%,10)] (A/P,20%10)] CAUE = -16,652,000 - NO ES RENTABLE b) 70% INGRESOS= 800*365*140= 40,880,000 CAUE= [40,880,000 + 10,000,000 [20,000,000+110,000,000(A/P,20%,10)] CAUE = -4972,000 NO ES RENTABLE c) - [20,000,000 + 110,000,000 (A/F, 20%, 10)] - 80% INGRESOS= 800*365*160= 46,720,000 CAUE= [46,720,000 + 10,000,000(A/F, 20%, 10)] - [20,000,000+110,000,000(A/P, 20%,10)] CAUE = 868,000 SI ES RENTABLE d) 90% INGRESOS= 800*365*180= 52,560,000 CAUE= [52,560,000 + 10,000,000(A/F, 20%, 10)] - [20,000,000+110,000,000(A/P, 20%,10)] CAUE = 6,708,000 SI ES RENTABLE Valor Presente 1. Unos ingenieros propusieron la introducción de un elemento de equipo nuevo con la finalidad de incrementar la producción de cierta operación manual para soldar. El costo de inversión es de $250,000, y el equipo tendrá un valor de desecho de $50,000 al final del periodo de estudio de cinco años. La productividad adicional atribuible al equipo importará $80,000 por año, después de restar los costos de operación del ingreso que se genera por la producción adicional. Si la TMAR de la compañía es del 20% anual, ¿es buena esta propuesta? Utilice el método del valor presente. VP = I-E VP = [80000(P/A, 20%, 5) + 50000 (P/F,20%,5)] – [250000] VP = 9343 > 0 ES RENTABLE 2. Resolver el problema 1 del valor anual, utilizando el método del valor presente VP= [270000(P/A, 18%,12) + 50000(P/F,18%,12)] – [250000 + 200000 (P/F, 18%,6) VP= 1301024 – 324080 = 976944 > 0 ES RENTABLE VP = [205000(P/A, 18%,12) + 20000(P/F,18%,12)] – [110000 + 90000(P/F,18%,4) + 90000(P/F,18%,8) = VP = [205000(4.7932) + 20000(0.1372)] – [110000 + 90000(0.5158) + 90000(0.2660) = VP = 982606 + 2744 – 110000 – 46422 – 23940 VP = 804988 > 0 ES RENTABLE, se selecciona esta opción debido a que tiene más valor anual. 3. Un ingeniero mecánico contempla dos tipos de sensores de presión para una línea de vapor de baja presión. Los costos aparecen a continuación. ¿Cuál debería elegirse sobre la base de una comparación del valor presente a una tasa de interés de 16% anual? Tipo X Tipo Y Costo inicial, $ -7,650 -12,900 Costo de mantenimiento, $/año -1,200 -900 Valor de salvamento, $ 0 2,000 Vida, años 2 4 CP = E-I (ESCOGER LA ALTERNATIVA DE MENOR COSTO) CP = [1200(P/A, 16%,4) + 7650(P/F,16%,2) VP = CP = 16,693 CP = [900(P/A,1+6%,4) +12900] – [2000 (P/F,16%,4)] CP = 14,313 SE SELECCIONA EL TIPO “Y”, POR TENER MENOR COSTO 4. Una compañía está analizando la posibilidad de comprar un compresor. Para ello ya se han iniciado las investigaciones respectivas y los resultados obtenidos son los siguientes: Compresor I Compresor II Inversión inicial $100,000 $200,000 Gastos anuales 40,000 25,000 Valor de rescate 25,000 25,000 Vida 2 años 6 años Si la TMAR es de 20%, ¿qué alternativa debe seleccionarse por el método del valor presente. LA QUE TENGA MENOR COSTO PRESENTE CP= E-I CP= [40000(P/A,20%,6) + 100000 + 75000(P/F, 20%,2) + 75000(P/F,20%,4)] – [25000(P/F,20%,6)] CP = (40000 * 3.3255) + 100000 + (75000 * 0.6944) + (75000 * 0.4823) - (25000 * 0.3349) CP = 312900 CP= [(25000 (P/A,20%,6) +200000] – [25000(P/F,20%,6)] CP= (25000 * 3.3255) + 200000 – (25000 * 0.3349) CP= 274765 Se selecciona el compresor II debido a que tiene un menor costo presente 5. Resolver el problema 3 del valor anual, utilizando el método del valor presente. VP VPx = [[80000 + 3000 (A/G,16%,3)] (P/A,16%, 3) + 150000] – [20000(P/F, 16%, 3)] VPx = 335745 – 12814 = 322931 VPx = 322931 + 322931(P/F, 16%3) + 322931 (P/F, 16%,6) + 322931 (P/F,16%, 9) VPx= 747294.62 VPy = [[60000 + 2500 (A/G,16%,4)] (P/A,16%, 4) + 240000] – [32000(P/F, 16%, 4)] VPy = 417095.2798 -17673.6 = 399421.6 VPy = 399421.6 + 399421.6 (P/F, 16%4) + 399421.6 (P/F, 16%,8) VPy =741845.73 VPz = [[48000 + 1000 (A/G,16%,6)] (P/A,16%, 6) + 310000] – [36000(P/F, 16%, 6)] VPz = 365638.01-14774.4 = 350863.6 VPz = 350863.6 + 350863.6 (P/F, 16%6) VPz =494858.03 Se selecciona la alternativa Z debido a que tiene un menor costo presente 6. Un puente recién construido cuesta $10,000,000. El mismo puente necesitará una renovación cada 10 años a un costo de $1,000,000. Los costos de las reparaciones y mantenimiento se calculan en $100,000 cada año. Si la tasa de interés es del 5%, determine el costo capitalizado del puente. CC= 10,000,000 + 100,000*[ 7. 1 ] + 1,000,000* (A/F, 5%,10) *[ 0.05 1 ] = 13,590,000 0.05 Determine el costo capitalizado de $100,000 en el tiempo 0, $25,000 en los años 1 a 5 y $50,000 del año 6 en adelante. Aplique una tasa de interés de 10% anual. 1 CC= 100,000 + 25,000 (P/A,10%,5) + 50,000 *[ ] *(P/F,10%,5) = 505,220 0.10 100000 + 94770 + 310450= 505,220 8. Determine el costo capitalizado de una alternativa que tiene un costo inicial de $32,000, un costo de mantenimiento anual de $6,000 y un valor de rescate de $8,000 después de 4 años de vida. Aplique una tasa de interés de 14% anual. 1 1 CC=32,000 + 6,000 *[ ] + 24,000 (A/F, 14%,4) *[ ] = 109,691 0.14 9. 0.14 Un padre de familia desea depositar en un fideicomiso bancario cierta cantidad de dinero con el propósito de ayudar financieramente a su hijo. El padre desea depositar el dinero cuando su hijo cumpla 10 años. Este dinero permanecerá en el fideicomiso sin ningún movimiento (depósitosretiros) hasta que su hijo empiece a retirar dinero a partir de que cumpla 18 años. El padre estipula al banco que el joven podrá retirar $20,000 cada cumpleaños de por vida. ¿Cuánto debe depositarse en el fideicomiso (cumpleaños 10) si la tasa de interés es del 10% anual? 1 CC= 20,000 [ ]= 200,000 0.10 CC= 200,000 (P/F, 10%,8) = 93,300 10. Considere a un hombre jubilado que comienza a cobrar los beneficios de su seguro social a los 60 años de edad. El cheque mensual sería de aproximadamente $2,160. Suponiendo una tasa de interés del 6% mensual, responda las siguientes preguntas: a. Si vive 20 años después de su retiro, ¿cuál sería el beneficio total equivalente recabado? b. Si vive 40 años después de su retiro, ¿cuál sería el beneficio total equivalente recabado? c. Suponga que vive para siempre. ¿Cuál sería la suma total acumulada? Ahora, comparando la respuesta con la del inciso b, ¿qué podría usted concluir? a) P= 2,160 [ b) P= 2,160 [ c) (1 + 0.06)240−1 0.06 ( 1+0.06)240 (1+ 0.06)480 −1 0.06 ( 1+0.06)480 1 CC= 2,160 [ 0.06 ] = 35, 999.96 ] = 36,000 ] = 36,000 TIR 1. Una persona contrató su servicio telefónico domiciliario y en el momento del contrato adquirió unas acciones de la empresa de $1,200. Esta persona no cobró los intereses en ningún periodo; después de ocho años un comprador le ofrece $3,350 por las acciones. Si decide vender las acciones, ¿qué tasa de interés anual habrá ganado a lo largo de los ocho años? F=P (F/P, i%, n) 3350 = 1200 (F/P, i%, 8) 2.7916 = (F/P, i%, 8) 2.7917 = (1+i) ^8 (2.7917) ^1/8 = 1 + i I= 13.69% 2. Una persona invierte $8,464 a cambio de recibir $3,000 al final del año 1, $3,500 al final del año 3, $4,000 al final del año 4 y $5,000 al final del año 5. ¿Cuál es la tasa de interés que recibirá por su inversión? VP=0=I-E VP= [3,000(P/F, i%,1) + 3500(P/F, i%, 3) + 4000(P/F, i%, 4) + 5000 (P/F, i%, 5)] – 8464=0 Si al hacer las operaciones da 0, esa tasa de interés es. I% =10% - Vp = 2729 I%, 15% - Vp = 1219 I%, 20% - Vp = 0.05 Considere un proyecto de inversión con los siguientes flujos de efectivo neto: Año Flujo neto de efectivo 3. 0 -$12,000 1 $2,500 2 $5,500 3 X 4 X ¿Cuál sería el valor de X si la TIR del proyecto es del 23%. VP = [2500 (P/F, 23%,1) + 5500 (P/F, 23%,2) + X(P/F,23%,3) + X(P/F,23%,4)] – 12000 = VP = [5668 + 0.5370x + 0.4369x] – 12000 =0 VP = 5668 + 0.9739X -12000 0.9739X = 12000 – 5668 0.9739X = 6632 X= 6500 4. Resolver el problema 1 del valor anual, por el método de la TIR incremental. BPv = [205,000(P/A, i%, 12) + 20,000 (P/F, i%,12)] – [110,000 + 90,000 (P/F, i%,4) + 90,000 (P/F, i%,8)] = 0 VPB = 804,988 I = TIR > TMAR - EL PROYECTO ES RENTABLE AÑO 0 1-12 4 6 8 12 B -110,000 205,000 -90,000 0 -90000 20,000 A -250,000 270,000 0 -200,000 0 50,000 B vs A -140,000 65,000 90,000 -200,000 90,000 30,000 I%=18% VP= 0 = I-E = [65,000(P/A, i%,12) +90,000 (P/F, i%, 4) + 90,000(P/F, i%,8) + 30,000 ( P/F, i%,12)] - [140,000 + 200, 000 (P/F, i%, 6)] = 0 VP = 171,956 Como TIR es mayor a la TMAR, seleccionamos A TIR = 47% >TMAR =18% 5. Un laboratorio tiene actualmente un proceso de liofilizado de vitaminas, y está evaluando la conveniencia de remplazarlo por uno nuevo. A continuación de dan los flujos de efectivo de las dos alternativas. Año Proceso actual Proceso nuevo 0 0 -$138,138 1 -$120,000 -$120,000 2 -$120,000 -$100,000 3 -$120,000 -$80,000 4 -$120,000 -$70,000 5 -$130,000 -$70,000 6 -$130,000 -$70,000 7 -$130,000 -$70,000 8 -$130,000 -$70,000 El proceso actual no tiene valor de rescate, y el proceso nuevo podría venderse en $25,000 al final de su vida útil de 8 años. Suponiendo una TMAR del 12% y usando el método de la TIR incremental, determine si debe remplazarse el actual proceso de liofilizado. Actual-Nuevo Año 0 1 2 3 4 5-8 8 Actual 0 -120,000 -120,000 -120,000 -120,000 -130,000 0 Nuevo -138,138 -120,000 -100,000 -80,000 -70,000 -70,000 25,000 Actual Vs Nuevo -138,138 0 20,000 40,000 50,000 60,000 25,000 VP = 0 = I-E VP = 0 = [20,000 (P/F, i%, 2) + 40,000 (P/F, i%, 3) + 50,000 (P/F, i%, 4) + 60000(P/F, i%, 5) + 60,000 (P/F, i%, 6) + 60,000 (P/F, i%, 7) + 85,000 (P/F, i%,8)] – 138,138 =0 I TMAR = 12% TIR = 21% > TMAR =12% CONVIENE MÁS EL NUEVO 6. Determine cuál de las dos máquinas siguientes debería elegirse usando un análisis incremental, si la TMAR es de 18% anual. Costo inicial, $ Costo anual, $/año Valor de salvamento, $ Vida, años Semi – Auto Omitir Comparación Año 0 1-6 3 6 Semi -40,000 -100,000 -35,000 5,000 Semiautomática -40,000 -100,000 5,000 3 Automática -90,000 -85,000 0 11,000 Automática -90,000 -85,000 11,000 6 SEMI Vs AUTO -50,000 15,000 35,000 6,000 Tmar =18% I = TIR = 36% > TMAR=18% SELECCIONAR LA ATOMATICA 7. Los flujos de efectivo incrementales para las alternativas M y N se presentan en seguida. Determine cuál debería elegirse usando un análisis de tasa de rendimiento con base en el valor presente. La TMAR es de 20% anual y la alternativa N requiere la mayor inversión inicial. B/T cap. 8. Año Flujo de efectivo incremental M vs N 0 $-25,000 1-9 +5,000 10 +8,000 0 1 2 3 4 5 6 7 8 9 10 TIR= -25000 5000 5000 5000 5000 5000 5000 5000 5000 5000 8000 16% TMAR=20%> TIR=16% Se selecciona M 8. Un ingeniero de Anode Metals está considerando los proyectos que se presentan en la tabla, todos los cuales se consideran con una duración indefinida. Si la TMAR de la compañía es de 13% anual, determine cuál debería seleccionarse si las alternativas son mutuamente excluyentes. Tasa de rendimiento Costo inicial, $ Ingreso anual, $ de la alternativa, % -20,000 +4,000 20 A -10,000 +2,000 20 B -15,000 +2,900 19.3 C -70,000 +10,000 14.3 D -50,000 +6,000 12 E TMAR=13% I=20%> TMAR= 13% AÑO 0 1-INDEF B -10,000 2,000 C -15,000 2,900 B Vs C -5,000 900 C -15000 2,900 A -20,000 4,000 C Vs A -5,000 1100 1 VP=900[ 𝐼 ] – 5000 1/i = 5000/900 I=900/5000 I= 18% TIR=18% > TMAR 13% SELECCIONAMOS C AÑO 0 1-INDEF 1 VP=1100[ 𝐼 ] – 5000 1/i = 5000/1100 I=1100/5000 I= 22% TIR=22% > TMAR 13% SELECCIONAMOS A AÑO 0 1-INDEF A -20000 4,000 E -50,000 6,000 A Vs E -30,000 2,000 A -20000 4,000 E -70,000 10,000 A Vs D -50,000 6,000 1 VP=2000[ 𝐼 ] – 30,000 1/i = 30,000/2,000 I=2,000/30,000 I= 6.66% TIR=6.66% < TMAR 13% SELECCIONAMOS A AÑO 0 1-INDEF 1 VP=6000[ 𝐼 ] – 50,000 1/i = 50,000/6,000 I=6,000/50,000 I= 12% TIR=12% < TMAR 13% SELECCIONAMOS A Análisis de Recuperación 1. Una alternativa para producir un pesticida tendrá un costo inicial de $200,000 con un costo anual de $50,000. Se espera que los ingresos sean de $90,000 anuales. ¿Cuál es el periodo de recuperación si a) i=0% y b) i=15% anual? a) N= 5 años para recuperar los $200,00 b) I= 15% Final del primer año -200,000 (F/P, 15%, 1) =- 230,000 El saldo de la inversión sería: -230,000 + 40,000 = -190,000 Final del segundo año -190,000(F/P, 15%,1) = -218,500 El saldo de la inversión sería: -218,500 + 40,000 = -178,500 Final del tercer año -178,500 (F/P, 15%, 1) = -205,275 El saldo de la inversión sería: -205,275 + 40,000 = -165,275 Final del cuarto año -165,275 (F/P, 15%, 1) = -190,066.25 El saldo de la inversión sería: -190,066.25 + 40,000 = -150066.25 Final del quinto año -150066.25 (F/P, 15%, 1) = -172576.18 El saldo de la inversión sería: -172576.18 + 40,000 = -132576.18 Final del sexto año -132576.18 (F/P, 15%, 1) = -152462.61 El saldo de la inversión sería: -152462.61 + 40,000 = -112462.61 Final del séptimo año -112462.61 (F/P, 15%, 1) = -129332 El saldo de la inversión sería: -129332 + 40,000 = -89332 Final del octavo año -89332 (F/P, 15%, 1) = -102731.8 El saldo de la inversión sería: -102731.8 + 40,000 = -62731.80 Final del noveno año -62731.80 (F/P, 15%, 1) = -72141.8 El saldo de la inversión sería: -72141.8 + 40,000 = -32141.58 Final del décimo año -321411.58 (F/P, 15%, 1) = -36962.8 El saldo de la inversión sería: -36962.8 + 40,000 = 3037.18 J&M manufacturing planea adquirir una nueva máquina de ensamblaje por $30,000 para automatizar una de sus operaciones de manufactura actuales. Hacer que instalen una nueva máquina costará $2,500 más. Con la máquina nueva J&M espera ahorrar $12,000 en costos operativos y de mantenimiento. La máquina durará cinco años, con un valor de rescate, con un valor de rescate esperado de $5,000. a. Cuánto tiempo tomará recuperar la inversión (más el costo de instalación) I=0% N= 2.7 años o 3 años b. Si la tasa de interés de J&M es del 14%, determine el periodo de recuperación. -32,500 (1.14) + 12,000 = -25050 -25,050 (1.14) + 12,000 =- 16557 -16557 * 1.14 +12,000 = -6874.98 -6874.98 (1.14) + 12,000 = 4162.52 N= 4 AÑOS 3. Resolver el problema 1 del valor presente por el método de recuperación de la inversión. Indique en que año se recupera la inversión. -250,000 (1.20) + 80,000 = -220000 -220000(1.20) + 80,000 = -184000 -184000 (1.20) + 80,000 = -140800 -140800 (1.20) + 80,000 = -88960 -88960 (1.20) + 130,000 = 23248 N= 5 AÑOS 2. Beneficio/Costo 1. La dependencia de desarrollo urbano de una ciudad está analizando modernizar cierto boulevard que con los años el tráfico vehicular se ha vuelto conflictivo. Según estadísticas de tránsito municipal hay en promedio 100 accidente de tránsito al año. En promedio el costo de estos accidentes automovilísticos es de $20,000 por accidente. Según el estudio de factibilidad realizado por el municipio se requiere una inversión inicial de $15 millones para la modernización del boulevard. Esto permitiría reducir el número de accidentes a tan sólo 10 por año. Se estima que para la operación y mantenimiento del boulevard se desembolsaría $100,000 anuales (limpieza, señalamientos y alumbrado). Puesto que la operación de este programa compartirá fondos con otros proyectos de la ciudad, se destinarán $200,000 para apoyo de dichos proyectos. El gobierno municipal contempla un horizonte de 20 años. Emplee el método B/C para determinar si la modernización del boulevard se justifica en términos económicos. El gobierno municipal utiliza una tasa del 10% anual para evaluar sus inversiones. Beneficio económico= 1,800,000 Costo= 20, 000 Inversión = 15,000,000 Costo de mantenimiento = 100,000 y 200,000 B/C = 1800000−200000 1761900+100000 = 0.86 B/C > 1 SE ACEPTA EL PROYECTO B/C < 1 SE RECHAZA EL PROYECTO Inversion = 15,000,000 (A/P, 10%,20) Inversion = 1,761,900 2. Los flujos de efectivo relacionados con un proyecto del sector gubernamental se distribuyen de la siguiente manera: costos= $550,000 anuales; beneficios= $600,000 anuales; contrabeneficios = $90,000 anuales. Determine la razón B/C. B/C = 600,000−90,000 550,000 = 0.927 B/C < 1 SE RECHAZA EL PROYECTO 3. Se espera que una norma propuesta relacionada con la eliminación de arsénico del agua potable tenga un costo anual de $200 por vivienda. Si se supone que hay 80 millones de viviendas en el país, y que la norma salvará 10 vidas cada año, ¿Cuál sería el valor de una vida humana para que la razón B/C fuera igual a 1.0? Beneficio =10 Costo de inversión = 80,000,000 * 200 = 16,000,000,000 VV * 10 / 16,000,000,000 = 1 VV = 16,000,000,000 / 10 = 1,600,000,000 El valor de la vida humana debe ser de 1,600,000,000