Transformaciones de Similitud

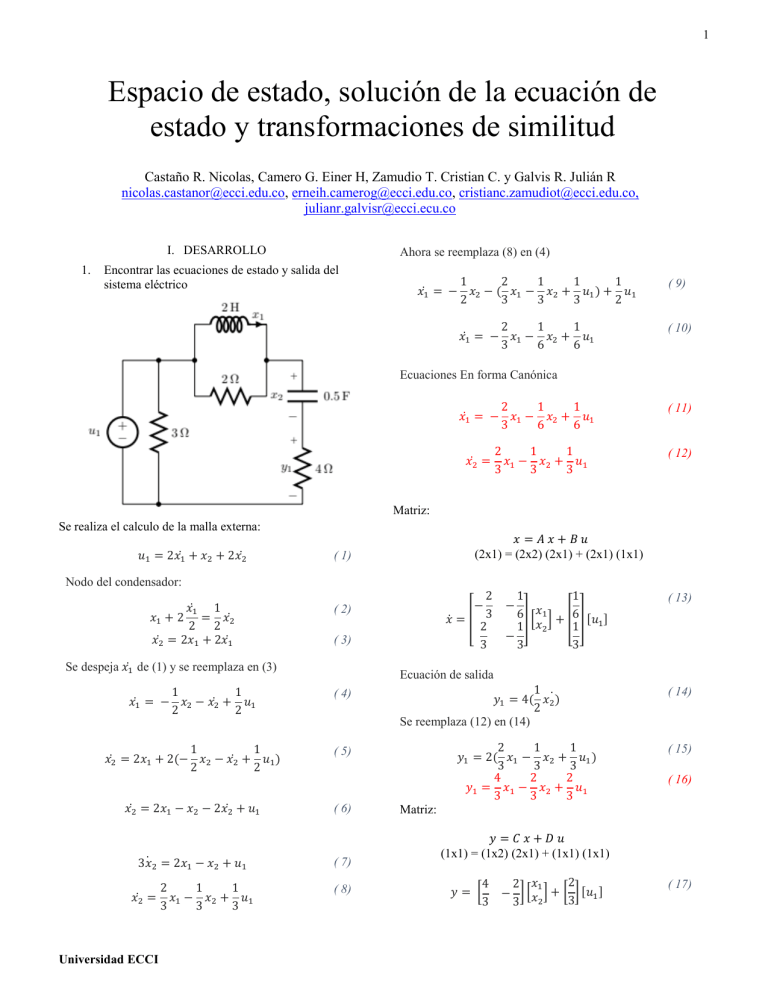
1
Espacio de estado, solución de la ecuación de
estado y transformaciones de similitud
Castaño R. Nicolas, Camero G. Einer H, Zamudio T. Cristian C. y Galvis R. Julián R
nicolas.castanor@ecci.edu.co, erneih.camerog@ecci.edu.co, cristianc.zamudiot@ecci.edu.co,
julianr.galvisr@ecci.ecu.co
I. DESARROLLO
1.
Ahora se reemplaza (8) en (4)
Encontrar las ecuaciones de estado y salida del
sistema eléctrico
1
2
1
1
1
𝑥1̇ = − 𝑥2 − ( 𝑥1 − 𝑥2 + 𝑢1 ) + 𝑢1
2
3
3
3
2
( 9)
2
1
1
𝑥1̇ = − 𝑥1 − 𝑥2 + 𝑢1
3
6
6
( 10)
Ecuaciones En forma Canónica
2
1
1
𝑥1̇ = − 𝑥1 − 𝑥2 + 𝑢1
3
6
6
𝑥2̇ =
2
1
1
𝑥1 − 𝑥2 + 𝑢1
3
3
3
( 11)
( 12)
Matriz:
Se realiza el calculo de la malla externa:
𝑢1 = 2𝑥1̇ + 𝑥2 + 2𝑥2̇
𝑥 =𝐴𝑥+𝐵𝑢
(2x1) = (2x2) (2x1) + (2x1) (1x1)
( 1)
Nodo del condensador:
𝑥1̇
1
𝑥1 + 2 = 𝑥2̇
2
2
𝑥2̇ = 2𝑥1 + 2𝑥1̇
( 3)
Se despeja 𝑥1̇ de (1) y se reemplaza en (3)
( 4)
1
1
𝑥2̇ = 2𝑥1 + 2(− 𝑥2 − 𝑥2̇ + 𝑢1 )
2
2
( 5)
3𝑥̇ 2 = 2𝑥1 − 𝑥2 + 𝑢1
𝑥2̇ =
Universidad ECCI
2
1
1
𝑥1 − 𝑥2 + 𝑢1
3
3
3
1
1
𝑥
1
6] [ ] + [6] [𝑢 ]
1
1 𝑥2
1
−
3
3
−
( 13)
Ecuación de salida
1
1
𝑥1̇ = − 𝑥2 − 𝑥2̇ + 𝑢1
2
2
𝑥2̇ = 2𝑥1 − 𝑥2 − 2𝑥2̇ + 𝑢1
2
𝑥̇ = [ 3
2
3
−
( 2)
( 6)
( 7)
( 8)
1
𝑦1 = 4( 𝑥2̇ )
2
Se reemplaza (12) en (14)
2
1
1
𝑦1 = 2( 𝑥1 − 𝑥2 + 𝑢1 )
3
3
3
4
2
2
𝑦1 = 𝑥1 − 𝑥2 + 𝑢1
3
3
3
( 14)
( 15)
( 16)
Matriz:
𝑦=𝐶𝑥+𝐷𝑢
(1x1) = (1x2) (2x1) + (1x1) (1x1)
𝑦= [
4
3
2
2 𝑥1
− ] [𝑥 ] + [ ] [𝑢1 ]
3
3 2
( 17)
2
2.
Forma canónica
Encontrar las ecuaciones de estado y
salida del filtro pasa bajos con
amplificador operacional.
1
𝑥1 ̇ =− 𝑥1 + 𝑥2 + 𝑢1
2
( 30)
1
𝑥2̇ = 𝑥1 0𝑥2 + 0𝑢1
4
( 31)
Matriz
𝑥 =𝐴𝑥+𝐵𝑢
(2x1) = (2x2) (2x1) + (2x1) (1x1)
1
𝑥̇ = [ 2
1
4
−
( 32)
1 𝑥
1
1
] [𝑥 ] + [ ] [𝑢1 ]
2
0
0
Salida:
LCK
𝑖1 + 𝑖4 = 𝑖2 + 𝑖3
𝑦1 = 𝑣𝑜𝑢𝑡 = 𝑖4 + 𝑥1
( 18)
( 33)
Reemplazos (24) en (33)
Malla 1
𝑢1 = 𝑖1 + 𝑥1
( 34)
( 19)
Reemplazamos (22) en (34)
Malla 2
𝑥1 = 2 𝑖3
( 20)
𝑦1 = 4
𝑥1
+ 𝑥2 + 𝑥1
4
( 35)
𝑦1 = 2𝑥1 + 𝑥2
𝑖3 = 2𝑥2̇
( 21)
𝑥1
4
( 22)
𝑥2̇ =
Matriz
𝑦=𝐶𝑥+𝐷𝑢
(1x1) = (1x2) (2x1) + (1x1) (1x1)
Malla 3
2𝑖3 + 𝑥2 = 𝑖4
4𝑥2̇ + 𝑥2 = 𝑖4
3.
( 24)
𝑖1 = 𝑥1̇ + 2𝑥2̇ − 4𝑥2̇ − 𝑥2
( 25)
𝑖1 = 𝑥1̇ − 2𝑥2̇ − 𝑥2
( 26)
Se reemplaza (26) en (19)
1
𝑢1 = 𝑥1̇ − 𝑥1 − 𝑥2 + 𝑥1
𝑥1
1] [𝑥 ] + [0][𝑢1 ]
( 27)
( 37)
2
Encontrar la solución de la ecuación de estado, si u
(t) es el escalón unitario y t0 = 0
−1
𝐴=[
3
Se Despeja i1 de (18) y se reemplaza (24)
𝑢1 = 𝑥1̇ − 2𝑥2̇ − 𝑥2 + 𝑥1
𝑦 = [2
( 23)
Se reemplaza (21) en (23)
( 36)
0
]
1
1
𝐵= [ ]
0
2
𝑥(𝑡0 ) = [ ] 𝑐 = [1
−1
1]
la solución de 𝑒 𝐴𝑡 , se debe realizar por Cayley-Hamilton.
∅( λ) = |𝐴 − 𝜆 × 𝐼|
𝐼 = 𝑒𝑦𝑒(4)
𝑃 = det(𝐴 − 𝜆 × 𝐼)
𝑒𝑥𝑝𝑎𝑛𝑑(𝑝)
( 28)
2
1
𝑥1 ̇ =− 𝑥1 + 𝑥2 + 𝑢1
2
Universidad ECCI
( 29)
∅(𝜆) = 𝜆2 + 2𝜆 + 1
( 38)
3
Se hallan las raíces:
4.
𝜆1 = 1 ; 𝜆2 = −1
( 39)
𝑔(𝜆) = 𝑎1 𝜆 + 𝑎0
( 40)
𝑒−𝑡 = −𝑎1 + 𝑎0
𝑒𝑡 = 𝑎1 + 𝑎0
( 41)
𝑒 𝑡 + 𝑒 −𝑡
𝑒 𝑡 − 𝑒 −𝑡
𝑎0 =
; 𝑎1 =
2
2
( 42)
𝑔(𝐴) =
c.
𝑒 𝑡 − 𝑒 −𝑡
𝑒 𝑡 + 𝑒 −𝑡
∗𝐴+
∗𝐼
2
2
( 43)
𝑒
𝑒 −𝑡
3𝑒 −𝑡
= [3𝑒
−
2
2
0
𝑡
𝑒
( 44)
−𝑡 ]
𝑒 −(𝑡−𝑡)
3
+ ∫ (3
× 𝑒 (𝑡−2) − 𝑒 (𝑡−𝑡)
0
2
2
𝑒 −𝑡
𝑥1(𝑡)
(
) = (3 𝑡 3 𝑡
𝑥2(𝑡)
𝑒 − 𝑒
2
2
0
1
𝑒 (𝑡−𝑡)
0
𝑒
𝑡) × (
0
) × ( ) × (1)𝑑𝑧
1
0
2
)+(
)
−1 + 𝑒 𝑡
−1
( 46)
( 48)
−𝑒
𝑦(𝑡) = (2𝑒 𝑡
−𝑡 )
0
)
𝑒 (𝑡−𝑡)
+ (1
0
−1
0
× ( ) × (1)𝑑𝑧
1
1) × (−1 + 𝑒 𝑡 )
−𝑒 −𝑡 ) + (−1 + 𝑒 𝑡 )
8 −9
−9
−5
𝑃=[
−5
1
1
0
𝐴2 𝐵
𝐴𝐵
0
𝐶𝑂 = [0
0
1
−5
1
0
0
Universidad ECCI
−𝑒 −𝑡 − 1)
( 52)
4
2
3
2
25
15
21
10
1
0]
0
0
( 53)
𝐴3 𝐵 )
( 54)
158
93 ]
133
60
𝑀 = 𝑃 ∗ 𝐶𝑂
( 49)
−3 5
5
𝑀=[ 0
1 6
0 −9
( 55)
4
2
3
−3
0
0]
0
1
( 50)
𝐴𝑀 = 𝑀−1 ∗ 𝐴 ∗ 𝑀
𝑦(𝑡) = (3𝑒 𝑡
0)
∅( λ) = |𝐴 − 𝜆 × 𝐼|
𝐼 = 𝑒𝑦𝑒(4)
𝑃 = det(𝐴 − 𝜆 × 𝐼)
𝑒𝑥𝑝𝑎𝑛𝑑(𝑝)
𝐶𝑜 = (𝐵
𝑦(𝑡) = 𝑐 × 𝑒 𝑎(𝑡−𝑡) × 𝑥(𝑧𝑜) +
𝑦(𝑡) = (2𝑒 𝑡
𝐶 = (1
CANONICA CONTROLABLE
( 47)
3
+𝑐 ∫ (3
× 𝑒 (𝑡−2) − 𝑒 (𝑡−𝑡)
0
2
2
0
𝐵 = ( 0)
1
1
( 45)
−𝑡
𝑥1(𝑡)
(
) = ( 𝑡 2𝑒 −𝑡
)
𝑥2(𝑡)
3𝑒 − 3𝑒 − 1
𝑒 −(𝑡−𝑡)
3 4
3 2)
3 3
0 2
∅(𝜆) = 𝜆4 − 5𝜆3 − 9𝜆2 + 8𝜆 + 3
𝑥(𝑡) = 𝑒 𝑎(𝑡−𝑡) × 𝑥(𝑧𝑜) +
1
1 2
𝐴 = ( 1 −1
1 1
1 1
𝐷 = (0)
Resultado en Matlab
𝐴𝑡
Encontrar la forma canónica controlable y observable
del sistema asignado
( 51)
0
𝐴𝑀 = [ 0
0
−3
1
0
0
−8
0
1
0
9
( 56)
0
0]
1
5
4
𝐵𝑀 = 𝑀−1 ∗ 𝐵
( 57)
0
𝐵𝑀 = [0]
0
1
𝐶𝑀 = 𝐶 ∗ 𝑀
𝐶𝑀 = [−4
( 58)
1
0]
0
0
1
−5
0
0]
0
1
( 59)
0
1]
4
25
( 60)
−1
CANONICA OBSERVABLE
1
0
−5
1
𝑃=[
−9 −5
8 −9
1 0
𝑂𝑏 = [ 0 1
2 0
9 11
−1
0
3
15
(𝑃 ∗ 𝑂𝑏 )−1
5.7692
𝑀 = [ 2.9615
4.7692
2.0385
0.8462
0.8077
0.8462
0.1923
( 61)
0.2308 0.1538
0.0385 0.1923 ]
0.2308 0.1538
−0.0385 −0.1923
𝐴𝑀 = 𝑀−1 ∗ 𝐴 ∗ 𝑀
5 1
𝐴𝑀 = [ 9 0
−8 0
−3 0
0
1
0
0
( 62)
0
0]
1
0
𝐵𝑀 = 𝑀−1 ∗ 𝐵
( 63)
0
𝐵𝑀 = [ 0 ]
−1
−4
𝐶𝑀 = 𝐶 ∗ 𝑀
𝐶𝑀 = [1
Universidad ECCI
0
0
( 64)
0]