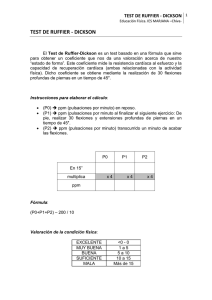
Validez del Test de Ruffier en la Valoración del Esfuerzo Físico
Anuncio

“VALIDEZ DE RUFFIER TEST EN VALORACIÓN DE LA RESISTENCIA A EL ESFUERZO FÍSICO”, Resumen La prueba de Ruffier se utiliza para evaluare la resistencia de un corazón al esfuerzo físico y es4destinado a adultos. El objetivo de la investigaciónch en este documento fue crear un modelo de la5Prueba de Ruffier adaptada al deporte escolar y la educación física, es decir, para alumnos de 6 a 16 años. Eso6se demostró que dos modelos bien conocidos de corrección de la prueba de Ruffier a la edad de los jóvenes7los pacientes estaban en conflicto y por lo tanto no rEleable en la práctica de la educación física.8Se utilizaron modelos matemáticos y simulación por computadora. en esta investigación. inter y9se emplearon extrapolaciones de las escalas de evaluación basadas en el índice de Ruffier.10Los cálculos se realizaron con MS ExcelVRy MathCADVR. Dos métodos de adaptación de11la evaluación de la prueba de Ruffier para el estado de salud de pacientes jóvenes waquí propuesto. En una de12los métodos, el valor del índice de Ruffier fue corregido, y en otro, la escala de13la evaluación fue igualmente. un valor normal de la frecuencia cardíaca en reposo fue aceptareducado como un14parámetro de corrección en ambos modelos. En general al, el modelo propuesto de corrección de la15cursos de evaluación de prueba una diferencia estadísticamente significativa con un resultado correspondiente dieciséis determinado según el modelo original ( p < 0,001). El resultados de esta corrección17mostró un aumento considerable facilidad en un grupo básico de educación física (física normal).18actividad) y una disminución en un grupo de curso de preparación (disminución físicaactividad física) y una19grupo especial (mala actividad física). Este la corrección por edad aumentó la validez de la puntuación de la prueba20para niños y adolescentes a un nivel de originalmente prueba la validez de la puntuación para adultos. Palabras claves:prueba, esfuerzo físico, resistencia, validez Introducción Hace más de 60 años, el Dr. J. Ruffier hizo una prueba de resistencia24 de un corazón al esfuerzo físico [ 1 ]. Debido a que la prueba es válida, fácilmente25 reproducible y simple, no requiere ningún equipo pero26 un temporizador. Como tal, es bastante popular en educación física, deportes27 medicina, rehabilitación, etc. [ 2 – 4 ].28 Ruffier usó su prueba originalmente para adultos, pero posteriormente29 la prueba se utilizó tanto para niños como para adolescentes. Desde el30 muy al comienzo del año académico 2009–2010, según31 el Ministerio de Educación y Ciencia de Ucrania [ 5 ], el Ruffier32 se introdujo en Ucrania como un método formal de33 clasificación en las categorías del estado de salud de 6–16-Alumnos de 34 años. Según estas categorías, un programa deSe corrigieron 35 lecciones de educación física. Como resultado, un gran36 parte de los alumnos (en algún lugar más de la mitad) apareció en el37 grupo más débil (llamado "especial") con un valor nominal (casi cero)38 nivel de actividad física. Incluso algunos jóvenes deportistas estaban39 “condenados” a un grupo especial según los resultados de la Ruf-Prueba de 40 fuegos. Profesores de educación física, alumnos y padres41 necesitaba tener una explicación del problema y una manera para su42 solución.43 El Ministerio de Educación y Ciencia de Ucrania [ 5 ]44 dirigió la prueba de Ruffier en su forma original cuando un valor de la45 índice correspondiente se calcula de la siguiente manera: R ¼ 4 norte 0 + norte 1 + norte 2ðÞ 20010 (1)46 donde:47 norte 0 ¼ un número de latidos del corazón durante 15 s en reposo,48 n 1 ¼ un número de latidos durante 15 s justo después del final de la49 esfuerzo (30 sentadillas durante 45 s), y50 norte 2 ¼ un número de latidos durante 15 segundos en 45 segundos después la final de51 el esfuerzo.52 El Ministerio de Educación y Ciencia de Ucrania [ 5 ]53 definió un valor de índice de un grupo especial igual a 10 puntos y54 mayor. Por ejemplo, un alumno de 6 años con un corazón normal55 ritmo alrededor de 102 latidos por minuto obtiene un valor del índice mayor56 que 10,6 y aparece en un grupo especial. la causa de la57 resultados más débiles de los niños según la prueba de Ruffier fue en58 utilizando el procedimiento de prueba original y una escala de evaluación59 estructurado para adultos. Los niños y adolescentes sanos tienen una60 frecuencia cardíaca mayor que los adultos. Desde el nacimiento hasta los 16 años, un normal61 la frecuencia cardíaca disminuye aproximadamente 1,5 veces [ 6 ].62 Se han propuesto tres métodos con el fin de dar cuenta63 una edad en la prueba de Ruffier. Según un primer método, el esfuerzo64 para niños debe reducirse de 30 a 20 sentadillas [ 7 ]. Ahí65 son dos las dificultades de aplicar este método para resolver el66 problema. Este método no define un modelo esencial de67 correlación entre el esfuerzo y la edad y en conjunto la68 El Ministerio de Educación y Ciencia de Ucrania [ 5 ] prescribió solo69 30 sentadillas como esfuerzo.70Se propuso una corrección diferencial del valor del índice71con un segundo método por Dykhan [ 8 ]. Según este método,72el valor calculado del índice (Eq 1 ) debe incrementarse en 173o 2 puntos o disminuido de 1 a 5 puntos correspondientes a la74años. Sin embargo, este método no es suficientemente aceptable porque75el aumento del valor del índice con el uso de una escala clásica de evaluación76ment (asignado para adultos) hace que los puntajes de los alumnos para una cierta edad77(10–16 años) bastante malo, es decir, lejos de la realidad.78De acuerdo con el tercer método [ 9 ], el límite del índice de Ruffier79arios entre los niveles de salud en la tabla original de evaluación80ment para adultos se incrementaron en 1,5-6,0 puntos proporcionalmente81a la edad de 7–15 (y más) años. La idea del método.82era bastante razonable y mostró una manera de resolver un problema de83teniendo en cuenta la edad de los pacientes jóvenes. valores de la84El índice de Ruffier (Eq 1 ) debe incrementarse a un nivel más alto para85paciente más joven. Valores correspondientes de límites para los 686y los niños de 16 años podrían calcularse usando un lineal87interpolación. Sin embargo, hay dos características débiles en el88método. Para el primero, se calculó el índice de Ruffier en base a89frecuencia cardíaca, pero la corrección de los valores de los límites de acuerdo con90este método se basó en la edad. La pregunta es: si un91frecuencia cardíaca es inversamente proporcional a una edad en el rango de92¿Pacientes de 7 a 15 años? Para el segundo, ¿por qué el rango de93los puntos de índice elegidos para ser 6 puntos?94El objetivo de la investigación fue crear un modelo de Ruffier95prueba adaptada al deporte escolar y la educación física, es decir, para96Alumnos de 6 a 16 años. Métodos Los resultados de los alumnos de la prueba de Ruffier se recuperaron de Internet99datos en los sitios web oficiales. Modelado matemático y com-100simulación por ordenador se utilizaron en la investigación. Inter- y extrapo-101las escalas de evaluación basadas en el índice de Ruffier fueron102empleado. Los cálculos se realizaron utilizando MS Excel y Math-103Programas informáticos CAD. En los modelos de salud de los alumnos104evaluación, se empleó una distribución normal y Excel105Se utilizaron las funciones NORMSDIST y NORMINV. Pearson106Se aplicó la prueba de chicuadrado y se calculó la función de Excel DISTR.CHI.107utilizados en el análisis de las hipótesis estadísticas sobre una existencia108tenencia de una totalidad general común con respecto a dos muestras109determinado de acuerdo con los modelos de distribución de alumnos en110niveles de salud y en grupos de clases de educación física.111Correlaciones de la frecuencia cardíaca y el índice de Ruffier versus la edad112fueron modelados aplicando polimonas algebraicas. sus coeficientes113se calcularon como una solución del sistema lineal de ecuaciones114usando la función 'lsolve' de MathCAD. Resultados Se diseñaron dos métodos para la adaptación del Ruffier117en la evaluación del estado de salud de pacientes de 6 a 16 años. El valor del índice de Ruffier se corrigió con uno de los119 métodos y una tabla de valoración se corrigió con otra120 uno. Un valor normal de la frecuencia cardíaca en reposo se aceptó como121 parámetros de corrección en ambos modelos. La idea de la primeraEl método 122 se tomó prestado del modelo del índice de Ruffier123 propuesto por Dykhan [ 8 ], y el segundo, por Guseva [ 9 ]. UN MODELO DE CORRECCIÓN DEL ÍNDICE DE RUFFIER En reposo, la frecuencia cardíaca normal en los niños es mayor y su126 reacción a un esfuerzo es menor que los adultos [ 7 ]. Por lo tanto, como primera127 estimación, alguien puede aceptar una correlación proporcional128 entre una frecuencia cardíaca en reposo y después de un esfuerzo en cualquier edad. Ahí-129 por lo tanto, se podría derivar una fórmula corregida del índice de Ruffier130 de la siguiente manera: R k ¼ f = k 20010 (2)131 donde:132 f ¼ 4 norte 0 + norte 1 + norte 2ðÞ,k ¼ðf p = f a Þ , f p ¼ una frecuencia cardíaca normal133 en reposo para la edad de un paciente, y134 f a ¼ frecuencia cardiaca normal en reposo para adulto (igual135 70 minutos 1).136 Como el coeficiente k > 1, el valor corregido de137 el índice de Ruffier (Eq 2 ) es menor que el original calculado138 con la ecuación 1 .139 Se realizó una aproximación funcional de la frecuencia cardíaca en función de la edad.140 derivado usando un polinomo algebraico de quinta potencia porque141 seis grados de la edad en el rango de 6 a 16 años generalmente son142 presentado en estudios correspondientes [ 6 ] donde HR es una frecuencia cardíaca en reposo, A es una edad medida en años.144 En correspondencia con el modelo (Eq 2 ), un nomograma lineal145 en el rango de la frecuencia cardíaca de los pacientes de 6 a 16 añosEl grupo 146 se presenta en la Fig. 1 . Es fácil notar que para un147 valor promedio de una suma de latidos del corazón ( f ¼ 300 marcado con un148 línea discontinua vertical con abscisas igual a 300) pacientes de149 Los niños de 6 a 8 años deben evaluarse como de “alto nivel” de salud150 ( R k ¼ 0,6–2,6), 10 años—a un nivel “bueno” ( R k ¼ 5,0), 12–14151 años—a un nivel “promedio” ( R k ¼ 7.1–9.0), y pacientes de152 16 años o más: a un nivel de salud "aceptable"153 ( Rk = 10,0 ). Uno puede leer los valores corregidos del índice en el154 puntos de cruce de líneas discontinuas horizontales y ordenadas.155 Según el Ministerio de Educación y Ciencia de Ucrania156 [ 5 ], se determinó que el valor del índice de Ruffier era igualado157 10, que podría ser aceptado para el grupo de edad de 16 años158 y mayores. Usando la Eq 1 original dirigida con el ucraniano159 Ministerio de Educación y Ciencia, solo se puede obtener una160 nivel de la evaluación de la salud para todas las edades, es decir, un “inferior a161promedio” que significa un grupo “especial” en educación física162lecciones 1Análisis comparativo del modelo de corrección (Eq 2 )164con un modelo de Dykhan [ 8 ] mostró una diferencia sustancial en165resultados. Por ejemplo, cuando el índice de Ruffier es igual a 10 puntos (un166valor crítico para adulto) una suma de valores de una frecuencia cardíaca (en reposo,167justo después del final del esfuerzo, y en 45 s después del final de la168esfuerzo) por Eq 1 se calcula igual a 300. Diferencia relativa169cia entre los valores del índice de Ruffier de acuerdo con estos dos170modelos se estimó con la siguiente fórmula (Apéndice):d R ¼ R D R kR D þ R k 200 % (4)171donde R D es un valor del índice de Ruffier corregido según172Modelo de Dykhan [ 8 ]. Valores de datos correspondientes para los jóvenes173pacientes, de 6 a 16 años de edad, mostraron diferencias sustanciales entre174este modelo en el rango 35 d R 175 % y el valor medio17574 %.176UN MODELO DE CORRECCIÓN DE LA ESCALA DE EVALUACIÓN177Usando las ecuaciones 1 y 2 , una correlación entre los valores de Ruffier178índice de límites entre los niveles de salud en la forma original179y en una forma corregida se derivó como una ecuación a continuación:R p ¼ kR a þ 20 k 1ðÞ (5)180dónde:181R p ¼ un valor del índice de Ruffier en forma corregida (para182el paciente joven), y183R a ¼ el valor del índice de Ruffier en la forma original (para184adultos).185Un nomograma que muestra una correlación entre los valores de186los lmites del ndice de Ruffier entre los niveles de salud es pre-187enviado en la Fig. 2 . Usando el nomograma, uno puede determinar188valores de los límites entre los niveles de salud desde el más bajo189al mas alto Por ejemplo, cuando un paciente tiene 10 años, dibuje190una vertical con la abscisa 10 (línea discontinua). en los puntos deHIGO. 1 Nomograma de la corrección de los valores del índice de Ruffier.J AL. EN VALIDEZ DE PRUEBA DE RUFFIER 3 cruce con líneas de nomograma (continuas), siga horizontal192 líneas (interrumpidas) para cruzar con ordenada y leer el193 valores de los límites. Un nomograma mostró claramente una disminución de194 valores de los límites frente al aumento de la edad del paciente.195 Valores exactos de los límites en función de la edad con unEn la Tabla 1 se presentan 196 pasos de un año según la ecuación 5 . Para197 ejemplo, si un paciente tiene 10 años, una frecuencia cardíaca normal en reposo198 es 84 minutos 1, por lo tanto k ¼ 1.2. La ecuación 5 devuelve valores como199 sigue: R p ¼ 21.4, 15.4, 11.8 y 8.2. Límites correspondientes200 valores entre los niveles de salud según el ucraniano201 Ministerio de Educación y Ciencia [ 5 ] son: R a ¼ 14.5, 9.5, 6.5,202 y 3.5 (ver línea inferior en la Tabla 1 ).203 DISTRIBUCIÓN DE LOS ALUMNOS EN LOS NIVELES DE SALUD204 Basado en una teoría de evaluación del movimiento humano [ 10 ] uno puede205 aceptan una distribución normal de los valores del índice de Ruffier. los206 rango M 6 2 SD de su valor cubre el interior de los niveles de207 evaluación de la salud de “inferior al promedio” a “superior al208promedio”, que aglutina al 95 % de todos los pacientes. De acuerdo a209al Ministerio de Educación y Ciencia de Ucrania, estos210los límites son iguales a 3.5 y 14.5, lo que conduce a los valores de211parámetros estadísticos: M ¼ 0 : 9 ; SD ¼ 2 : 75. Por lo tanto, la norma212La mala distribución de los pacientes en los niveles de salud debe ser:213un nivel alto—2.3 %, un nivel superior al promedio—15.9 %, un promedio214– 39.0 %, inferior al promedio—40.5 %, y bajo—2.3 %215( Cuadro 2 ). Un grupo básico de salud se forma con el primero y216segundo nivel juntos (18.2 %), un grupo de curso de preparación—217con alumnos de nivel medio de salud (39.0 %), y un grupo especial—218con un cuarto y un quinto juntos (42,8 %). Una distribución similar219de alumnos en grupos de lecciones de educación física se notó220desde el comienzo del año académico 2009-2010 en221Zaporizhza, una industria ciudad de 1 106en el sur de Ucrania [ 11 ].222Cerca del 12 % de los alumnos fueron admitidos a un grupo básico. si tomamos223en cuenta los alumnos que no fueron admitidos en un grupo básico224de acuerdo con otros resultados de la prueba de Ruffier (especialmente, otros225recetas médicas, aproximadamente 6 %-7 %), la distribución226cumplirá bastante bien con una curva normal.227Utilizando la corrección de los valores del índice de Ruffier según228a la ecuación 4 con un valor promedio de frecuencia cardíaca ( f ¼ 300), algo229se puede determinar para la edad de los alumnos de 6 a 16 años230los valores del índice oscilan entre 0,5 y 10,0 y el valor medio es igual231R k ¼ 5,25 puntos, que es 4,75 puntos menos que el del adulto232( R a ¼ 10). Aceptando una hipótesis de una distribución normal y233usando parámetros estadísticos corregidos ( M ¼ 9.00–4.75 ¼ 4.25,234SD ¼ 2.75), alguien puede obtener una distribución corregida a la edad235de los alumnos según los niveles de salud: un nivel alto—29.3 %, un236superior a la media: 41,5 %, media – 24,2 %, inferior a237un promedio— 5.1 %, y un nivel bajo—un 0.03 % (ver Tabla 2 ).238Así, en un grupo básico de salud se presentó el 70,7 % de los alumnos,239y en un grupo especial, el 5,1 % del alumnado.240Un “cuadro trágico” de la salud del alumno reflejado por el241instrucción del Ministerio de Educación de Ucrania y242La ciencia [ 5 ] se convirtió en un “cuadro común” cuando la propuesta243Se aplicó el modelo de corrección con respecto a una edad (Eq 5 ). A244diferencia sustancial entre estos dos modelos tuvo un245confirmación estadística capaz. Por ejemplo, una escuela típica tiene246alrededor de 600 alumnos en 11 pares de clases. Una hipótesis estadística cero247esis sobre una totalidad general común respecto a dos muestras248apropiados a los modelos deben ser rechazados con un alto nivel249de confianza: v 2 = 406, = 19, p < 0,001. Un resultado similar fueHIGO. 2 Nomograma de corrección de los valores de los límites entre los niveles desalud.TABLA 1 Evaluación del nivel de salud: 1 – bajo, 2 - pasable, 3 - promedio,4 – bueno, 5 – alto.Límites de los valores del índice de RuffierEntre los Niveles de SaludAños Antiguo 1–2 2–3 3–4 4–56 30,3 23,0 18,6 14,27 28,3 21,3 17,1 12,98 25,8 19,2 15,2 11,29 23,4 17,1 13,3 9.510 21,4 15,4 11,8 8.211 19,4 13,7 10,3 6.912 18,2 12,7 9.3 6.013 17,0 11,6 8.4 5.214 15,7 10,6 7.4 4.315 15,1 10,0 7.0 3.9dieciséis 14,5 9,5 6,5 3,5TABLA 2 Distribución de los alumnos en los niveles de salud (%).Nivel de Saludmodelo altoMás alto quePromedio PromedioMás bajo quePromedio BajoPrincipioa2.3 15.9 39.0 40,5 2,3ecuación 2 29.3 41.5 24.2 5.1 0.03tabla 1 21.8 46.2 27.7 4.3 0.01aMinisterio de Educación COPIA DE PRUEBA [JTE20160380]250 dado en cuanto a una distribución de los alumnos en los grupos de251 lecciones de educación física: v 2 ¼ 385, ¼ 11, p < 0,001.252 Con el propósito de estudiar un carácter de cambio de la dis-253 tributación de los alumnos en los niveles de salud y grupos de salud254 educación cursada por los valores del índice de Ruffier acompañados cor-255 , se tomó en cuenta la edad promedio de los alumnos de 11 años.256 consideración. Los límites del índice de los niveles de salud para257 esta edad son 6.9, 10.3, 13.7 y 19.4 (ver Tabla 1 ), y correspon-258 La distribución normal correspondiente de alumnos es: un nivel alto: 21,8 %,259 superior a la media—46,2 %, media—27,7 %, inferior260 que un promedio—4.3 %, y un nivel bajo—0.01 % (ver Tabla 2 ).261 Hay un 68,0 % de pacientes en un grupo básico de salud y262 4,3 %–en un grupo especial.263 Para el ejemplo se ha considerado una escuela ( n ¼ 600), una264 hipótesis estadísticas sobre una similitud de distribuciones en niveles265 de salud según el Ministerio de Educación de Ucrania y266 Science (2009) y al modelo de la corrección (ver Tabla 1 )267 debe rechazarse con un alto nivel de confianza: v 2 ¼ 384,268 ¼ 19, p < 0,001. Un resultado similar se dio con respecto a una distribución269 ción de alumnos en los grupos de lecciones de educación física:270 v 2 ¼ 373, ¼ 11, p < 0,001. Controversia, modelos de corrección271 (Eq 2 ) y la Tabla 1 mostraron una distribución suficientemente similar y272 para los niveles de salud ( v 2 ¼ 10, ¼ 19, p > 0.9), y para el273 grupos de lecciones de educación física ( v 2 ¼ 2.14, ¼ 11,274 p > 0,99).275 Una distribución corregida del nivel de salud no contradice276 dictan resultados de estudios médicos que son bastante sensatos. Por lo tanto,277 no hay razones para rechazar la prueba de Ruffier como método de278 evaluación del nivel de salud de los alumnos en relación con la educación física279 lecciones de cationes. Sin embargo, la prueba debe modificarse la contabilidad280 a un ritmo cardíaco normal propio de la edad de un paciente joven. A281 valor corregido del índice de Ruffier en la práctica de física282 la educación se podría proponer calcular utilizando el siguiente283 ecuación:R k ¼ Cn0 þ n 1 þ n 2ðÞ 20010 (6)284 donde C ¼ 4 = k es un coeficiente de corrección de edad (ver Eq 2 ) calculado285 lated como cuatro dividido por la relación del valor medio de normal286 FC en reposo de una población de pacientes jóvenes a la correspondienteValor 287 en adultos (70 lpm). Un valor del coeficiente es menor288 mientras que un valor de edad es menor ( Tabla 3 ). Para un joven de 16 años, el valor289 del coeficiente encuentra un número 4, y la ecuación 6 se convierte en el290 ecuación original 1 .291 Discusión En general, el modelo propuesto de corrección de la prueba de Ruffier293evaluación de los cursos de salud de los alumnos estadísticamente significativa294( p < 0.001) diferencia con el resultado correspondiente determinado295según el Ministerio de Educación y Ciencia de Ucrania296[ 5 ]. Los resultados de las correcciones mostraron un aumento considerable297(49 %–53 %) de un grupo básico de educación física y298disminución de un grupo de cursos de preparación (11 %–15 %) y un299grupo especial (37 %–39 %).300COMPARACIÓN DE DOS MODELOS DE CORRECCIÓN POR301DYKHAN Y GUSEVA [ 8 , 9 ]302Debido a que se emplearon dos formas diferentes de corrección en303estos modelos (reduciendo los valores del índice en el primer modelo y304multiplicación de una escala de evaluación en el segundo), es necesario305sario para convertir uno en otro. La idea de la conversión fue306basado en los resultados opuestos de la multiplicación de corrección o307reducción de los valores del índice de Ruffier y la manipulación correspondiente308lación con una escala de evaluación. El segundo modelo fue309convertida en la primera.310Una función de aproximación de la corrección de la edad del311El índice de Ruffier de Dykhan [ 8 ] se derivó usando un método algebraico312polinomo de tercera potencia (porque se usaron cuatro intervalos en313el modelo) de la siguiente manera:D R D ¼ 0 : 0171 A 3 0 : 5272 A 2 þ 4 : 5015 A 6 : 689 (7)314Debido a que una reducción constante era relativa a la edad, una reducción lineal315función de corrección de los valores del índice de Ruffier en un316El modelo de Guseva (2005) se derivó de la siguiente manera:D R G ¼ 0 : 75 A þ 11 : 25 (8)317Como medida cuantitativa de la diferencia de estos modelos, un318Se utilizó el parámetro relativo presentado por la siguiente ecuación:d Q ¼ Q D Q GQ D þ Q G 200 % (9)319donde Q D = G ¼ ðdre = dA Þ D R D = GRAMO ð UN Þ Þ = re R re = GRAMO ð 6 Þ . Correspondiente320datos en el rango de 6 a 15 años (–198 % d Q 46 %), y321en promedio ( re Qjj¼58 %), mostró una diferencia sustancial322entre estos dos modelos de corrección. Por lo tanto, estos bien-323los modelos conocidos de corrección de la prueba de Ruffier son contradictorios.324Sin embargo, el primer modelo de Guseva [ 9 ] tiene una ventaja325porque no subestima los resultados de la salud326evaluación de alumnos de 10 a 16 años, al igual que el modelo de327Dikhan [ 8 ].328VIGENCIA DEL MODELO DE EVALUACIÓN DE GUSEVA329La validez de los puntajes de las pruebas se refiere a la adecuación de la interpretación.330ing los resultados de una prueba [ 12 ]. Un valor inferior del índice de Ruffier331correspondiente a un nivel medio de salud de 15 años . Según el modelo de333 Guseva [ 9 ], se aumenta a 11,5 para los pacientes en el 13-14grupo de 334 años, a 13,0 para los pacientes de 11-12, a 14,5 para los335 pacientes de 9-10, y a 16,0 puntos para los pacientes de 7-8 años336 de edad. Es decir, estos valores aumentan de forma inversamente proporcional a la edad.337 con un paso constante de 1,5 punto cada dos años.338 Es razonable estimar una precisión del modelo con respecto a339 ing un ritmo cardíaco porque es un parámetro del índice de Ruffier. Cuando340 el índice es igual a 10 puntos, una suma de valores de la frecuencia cardíaca (en341 descanso, justo después del final del esfuerzo, y 45 s después del final de la342 esfuerzo) de la ecuación 1 se calculó como 300. El valor correspondiente343 del índice, corregido a un ritmo cardíaco normal de pacientes jóvenes,344 debe calcularse con la siguiente ecuación:R c ¼ 300 k 20010 (10)345 Con el objetivo de comparar los valores del índice (Eq 10 ) con los correspondientes346 valores calculados según el modelo de Guseva [ 9 ], el primero347 uno se escaló en el rango de 10 a 16 puntos y se denominó R s :R syo ¼ R si þ 1 þ 6 D R ciR c1 R c5(11)348 donde i = 1, 2, 3, 4; R s5 ¼ 10; República Dominicana cyo ¼ R cyo R ci + 1 ( Tabla 4 ).349 Un error promedio de un paso igual a 1.5 fue estimado por el350 expresión 0 : 25 P 4i ¼ 1 DR s _yo 1 : 5 ¼ 0,8. Este valor es mayor351 que la mitad del número 1.5, donde i ¼ 1, 2, 3, 4;352 DR s _yo ¼ R syo R syo + 1 .353 Diferencia relativa entre un real (1,5 puntos) y un cálculo354 valor lated (DR s ) de los pasos de intervalo de índice de Ruffier fueron estimados355 emparejado con lo siguiente:d R yo ¼ DR s _yo 1 : 5DR s _i + 1 : 5 200 % (12)356 Valores de datos correspondientes en el rango357 ( 203 d R i 55 %) y con la significar valor ( d ri _jj¼ 56 %)358 mostró una no correspondencia sustancial con la relación lineal359 nave entre el índice de Ruffier frente a la edad con un paso de 1,5360 puntos por 2 años según el modelo de corrección por361 Guseva [ 9 ]. Por lo tanto, este modelo no es suficientemente confiable para362 la evaluación de los resultados de la prueba de Ruffier.363 De esta manera, el modelo propuesto de índice de Ruffier (Eq 2 )364 hace válida una prueba correspondiente para niños y adolescentes.365Debido a que no se modificó el procedimiento de la prueba de Ruffier, no366no hubo razones para evaluar su confiabilidad. Confiabilidad de la prueba367puntajes es el grado en que una herramienta de evaluación produce resultados estables368y resultados consistentes. Es razonable evaluar la fiabilidad de la puntuación de la prueba369habilidad cuando se introducen pruebas nuevas o modificadas, pero Ruffier370la prueba se ha utilizado en medicina deportiva y educación física371durante más de 60 años [ 12 ].372Hay una patente sobre el nuevo método que respalda el modelo.373desarrollado en esta investigación [ 13 ]. Conclusiones Una versión original de la prueba de Ruffier y modelos conocidos376de su corrección no son aceptables para la evaluación de la377nivel de salud de los pacientes jóvenes. Un valor normal de la frecuencia cardíaca.378en reposo debe aceptarse como parámetro de la corrección. A379modelo de corrección propuesto de la prueba mostró un estadísticamente380diferencia significativa ( p < 0,001) con los resultados correspondientes381determinado de acuerdo con el modelo original. Un valor corregido382del índice de Ruffier en la práctica de la educación física podría383calcularse usando la ecuación 6 con un coeficiente de corrección de edad (ver384Tabla 3 ). La validez de la puntuación de la prueba para niños y adolescentes fue385mejorado gracias a un modelo modificado para el índice de Ruffier.386Esta corrección por edad aumentó la validez de la puntuación de la prueba para los niños.387y adolescentes a un nivel de validez de puntaje de la prueba original para388adultos389Debido a que la prueba de Ruffier es válida, fácilmente reproducible,390y simple, no necesita ningún equipo más que un temporizador, es391sigue siendo popular en la educación física y la medicina deportiva.392Dr. J. Ruffier hizo su prueba para adultos, pero posteriormente la prueba393Se utilizó para niños y adolescentes. Niños y adolescentes394mostró valores elevados del índice de Ruffier en comparación con395adultos Esto se debe a que una frecuencia cardíaca normal en reposo en la infancia396y la adolescencia es mayor que en la mayoría.397La ecuación original del índice de Ruffier (Eq 1 ) fue corregida398multiplicando la suma de los latidos del corazón por un corazón normal promedio399tasa en reposo de adultos y dividiendo por un corazón normal promedio400tasa en reposo de un paciente más joven que fue probado. Esta edad401ción aumentó la validez de la puntuación de la prueba para niños y adolescentes402centavos a un nivel de validez de puntaje de prueba original para adultos.