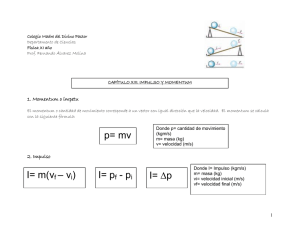
UNIVERSIDAD DE LOS LLANOS Facultad de Ciencias básicas e ingenierías Programa Ingeniería Electrónica INFORME DE LABORATORIO FÍSICA MECÁNICA Colisiones A. Uribe Rojas 1 , J. Ramos Reyes 2. 1. Cod:151004540 , Ingeniería Electrónica 2. Cod: 161004535, Ingeniería Electrónica Facultad de Ciencias Básicas e Ingenierías. Programa Ingeniería Electrónica II Resumen A partir del simulador en phet colorado en el apartado de colisiones en 2d se evidenciará el comportamiento de dos cuerpos que chocan entre ellos. En las colisiones, la energía y el momento lineal cambian, según la conservación de la energía de los cuerpos las colisiones se pueden clasificar en colisiones elásticas o colisiones inelásticas. Determinaremos cuál es la velocidad y el momento lineal antes de la colisión y después de ella ya sea elástica o inelástica. Palabras clave: colisiones, choques, conservación de energía, elásticas, inelásticas, momento lineal. 1. Introducción El término colisión o choque incluye cualquier interacción corta y fuerte entre cuerpos, en nuestro entorno es muy fácil observar todo tipo de choques, entre ellos están el choque de dos automóviles, de unas bolas de billar, de un meteorito con un planeta, entre otros. En las colisiones se puede ignorar cualquier fuerza externa al sistema ya que las fuerzas entre los cuerpos son mucho mayores a las fuerzas externas al sistema. Debido a que el sistema es aislado se puede asumir que el momento lineal antes de la colisión es el mismo momento lineal que va a haber después de la misma. Las colisiones pueden ser elásticas o inelásticas dependiendo de si la energía cinética es la misma antes y después del choque. los choques o colisiones elásticas son aquellas en las que no se gasta ni se gana energía mecánica en el choque, por ejemplo, en el choque de dos bolas de billar la colisión es casi elástica en su totalidad, ya que antes de la colisión las bolas se dirigen en cierto sentido con una energía cinética, al chocar con la otra bola por un instante esa energía se convierte en energía potencial elástica que hace que las bolas reboten y se dirijan en otro sentido con la misma energía cinética que inicialmente contaban. Colisiones Fuente [1]: Sears Zemansky (2009) - Física Universitaria vol.1 Para el análisis de un choque elástico entre dos cuerpos se sabe que la energía cinética tanto antes como después del choque se conservan, por lo cual: [1] Donde m1 es la masa del primer cuerpo y m2 es la masa del segundo, así mismo, v1 es la velocidad del primer cuerpo y v2 es la velocidad del segundo, mediante dicha ecuación se evidencia de forma clara la conservación de la cantidad de movimiento. A partir de esta misma ecuación y sabiendo los valores de las velocidades iniciales se puede despejar y aplicar casos de factorización para hallar cual es la velocidad final de cada uno de los cuerpos: [2] Velocidad final del cuerpo 1 después de la colisión elástica teniendo en cuenta las masas de cada uno de los cuerpos y la velocidad inicial antes de la colisión. [3] Colisiones Velocidad final del cuerpo 2 después de la colisión elástica teniendo en cuenta las masas de cada uno de los cuerpos y la velocidad inicial del cuerpo antes de la colisión. Las colisiones inelásticas son las que después del choque se evidencia menos energía cinética que antes del mísmo, en un choque inelástico la partícula choca con otra, se pegan y continúan en un mismo sentido como si fuesen un solo cuerpo, por ejemplo, es el caso de un tren que se dirige con cierta energía cinética hacia otro tren que está detenido, al chocar se genera una transferencia de energía en la cual se pierde parte de la energía cinética del primer tren y se transfiere al segundo para así terminar los dos moviéndose en la dirección en la que se dirigía inicialmente en primer tren pero ahora con menos energía cinética que al principio y por ende a una menor velocidad. Fuente [2]: Sears Zemansky (2009) - Física Universitaria vol.1 Cabe aclarar que no en todas las colisiones inelásticas los cuerpos deben quedar pegados, siendo así el caso de que dos partículas choquen, puede ser dos automóviles que colisionan y luego de perder energía hacen cierto desplazamiento en sentido contrario al inicial, en este caso, la colisión será inelástica debido a que en el choque hubo pérdida de energía cuando cada uno de los autos se deformaron en su parte frontal. Para hacer un análisis de la conservación de energía y de cantidad de movimiento es posible hacer una igualdad de la siguiente manera: [4] Donde m1 es la masa del objeto 1, m2 es la masa del objeto 2, v1 es la velocidad del objeto 1 y v2 es la velocidad del objeto 2, además los índices i y f corresponden a si la velocidad propuesta es la velocidad final o inicial, o sea, antes o Colisiones después de la colisión. A partir de allí podemos despejar para hallar la velocidad y así reemplazar en la fórmula de la cantidad de movimiento lineal [5] Ésta velocidad se halla con el propósito de saber cual es la cantidad de movimiento lineal que se obtiene en el sistema después de la colisión. [6] Donde p es la cantidad de movimiento lineal del sistema, v es la velocidad del sistema y m es la masa del cuerpo a evaluar. Todo lo anterior con respecto a colisiones ya sean elásticas o inelásticas fue analizado teniendo en cuenta que las dos partículas se dirigen la una en dirección a la otra y colisionan en algún punto, es de tener en cuenta que también pueden existir colisiones en las que uno de los objetos se encuentre en reposo antes de la colisión, sin embargo, siendo ese el caso, las fórmulas matemáticas son las mismas solo cambiando el valor de velocidad inicial de la partícula. 2. Sección experimental Se usó el simulador de Phet Colorado (Colisiones) para comprobar el comportamiento de las partículas al colisionar, dicho simulador permite la facilidad de crear casos ideales de colisiones totalmente elásticos e inelásticos y también permite crear situaciones en las que el sistema no actúa de forma perfecta sino con valores ingresados. Dicho esto, hay que conocer y tener presente que el simulador de colisiones en 2d nos permite variar algunos de los datos más importantes a la hora de hacer el análisis de colisiones, tales como lo son la masa del cuerpo, la velocidad con la que se mueve y la posición en el espacio, así se evidencia (en el modo de colisiones elásticas) que los valores iniciales serán los mismos que los valores finales, es decir, antes y después del choque. Adicionalmente el simulador web de Phet Colorado nos permite crear situaciones en las que el choque o colisión son totalmente inelásticas y al igual que en el caso de las colisiones inelásticas se puede modificar tanto la velocidad inicial de los objetos, la masa de cada uno de ellos y el lugar en el espacio, adicionalmente se permite escoger cuál será la dirección de las partículas en cuestión y si alguna de ellas se encuentra en reposo, es decir, con velocidad = 0. A partir de las observaciones del simulador, se obtienen los datos y se hace un análisis de lo que representan las colisiones y las diferencias entre cada tipo de colisión. 3. Resultados y análisis Para un sistema ideal de colisiones que se maneja en el simulador en la parte de introducción, la interacción entre dos partículas, M1 y M2. La masa mayor antes de hacer la colisión se dirige con una velocidad la cual se detiene cuando choca, ya que hubo una transferencia de movimiento, provocando un movimiento en la masa M2. Colisiones Fuente:https://phet.colorado.edu/sims/html/collision-lab/latest/collision-lab_en.html En el laboratorio “Explore 1D” se obtuvo un momento de colisión frontal entre varias Masas, donde en su análisis estas al chocar empezaron hacer una transferencia de movimiento consecutivamente debido que estas estaban entre unas mallas, como el juego del billar. Fuente:https://phet.colorado.edu/sims/html/collision-lab/latest/collision-lab_en.html Con el siguiente tipo de colisión se manejó el laboratorio del simulador “Explore 2D” en donde se manejó el mismo sistema anterior solo que al momento de la transferencia de movimiento esta variaba por que el espacio en el que estas estaban eran más amplio. Colisiones Fuente: https://phet.colorado.edu/sims/html/collision-lab/latest/collision-lab_en.html. Para el manejo del choque inelástico se usó una masa M1 la cual al ser lanzada a la M2, esta se “incrusta” en la masa haciendo que se vuelvan una M total, sin embargo referente a la diferencia entre los demás laboratorios, una característica es que siempre se debe mantener el momento. Fuente: https://phet.colorado.edu/sims/html/collision-lab/latest/collision-lab_en.html Para finalizar nuestro laboratorio se asumió en un sistema ideal inelástico, que consiste en que la partícula que viaja en dirección de la tierra es la masa “rosa” de 1.50Kg y la partícula que nos salva de esa colisión es la masa “azúl” que cuenta con 3.0Kg.. Colisiones Figura 1(Asteroide dirigido a tierra) Para solucionar la destrucción de parte de la tierra, nuestra masa colisionó con una velocidad de 1.20m/s para así repeler a la masa dos que se avecinaba con 0.74m/s. Figura 2(Asteroide dirigido a tierra) Tal y como se ve reflejado en la figura 2 nuestra cantidad de movimiento permaneció constante y se obtuvo una energía cinética total de 2.58J. La x presentada en la figura nombrada nos representa el valor de conservación del momento de 4.72Kg * m / s, este valor se obtuvo en el momento inicial y final, lo cual se observa al sumar los momentos de ambas masas. Colisiones Figura 3(Asteroide dirigido a tierra de forma inelástica) Para el manejo inelástico del sistema se hizo uso de una masa mayor que se avecinaba a la tierra, la cual se repele con una masa menor con una velocidad mayor a la del asteroide en un punto específico a esta para poder cambiar su dirección. Antes de la colisión se observó una energía cinética de 2.27J, un momento de 3.18kg(m/s). Los datos de las masas se pueden diferenciar en la figura 3. Figura 4(Momento de colisión entre asteroide y proyectil) Al analizar la colisión se puede entender que si se cumple el comportamiento de movimiento inelástico puesto que se vio una disminución de energía cinética, quedando 0.57J, al haber terminado la colisión estas cambian de dirección logrando salvar la tierra tal y como se observa en la siguiente figura 5. Colisiones Figura 5(Colisión salva a la tierra) 4. Conclusiones En las colisiones elásticas se conserva la energía cinética y se conserva el momento lineal puesto que no se producen deformaciones en los objetos ya que es una suposición planteada, aquello se evidencio en la primer parte de la práctica, además de ello se observó que los cuerpos después de colisionar parten con direcciones y velocidades distintas. En las colisiones inelásticas hay una pérdida de energía cinética como en el laboratorio de inelasticidad del simulador donde parte donde la energía inicial es de 2.27 J y la final de 0.57 J. En el movimiento el momento lineal se conservó durante la colisión, y después de la colisión las partículas se quedan unidas moviéndose con una velocidad y dirección en común debido a que son una sola masa por el choque que hubo entre ellas. 5. Referencias. [1] Zemansky, S. (2009). Física universitaria (Décimo segunda ed., Vol. 1). Young Freedman.