guia-de-ejercicios-bio compress

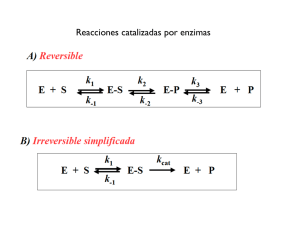
GUÍA DE EJERCICIOS BIO-REACTORES
Fundamentos de Ingeniería Bioquímica
IWQ-250
Profesores: Sergio Almonacid M. y Ricardo Simpson R.
2013
SAM/RS
1
I EJERCICIOS RESUELTOS (incluye solución desarrollada)
1. a) El ciclo celular es un conjunto ordenado de sucesos que conducen al crecimiento de la célula
y la división en dos células hijas.
a) Demuestre, matemáticamente, que la ecuación 1 se puede representar por una cinética de
primer orden teniendo en consideración que el tiempo de duplicación celular es constante:
(1)
Donde:
x : Concentración celular (g/L)
t : Tiempo (h)
 : Velocidad específica de crecimiento (h-1)
b) ¿Qué relación hay entre el tiempo de duplicación (o de generación) tD y la velocidad específica
de crecimiento, ?
2. Demuestre que para un Bio-reactor simple (1 etapa), operado en estado estacionario, se cumple
la siguiente relación (asumiendo x0 = 0):
 = D; (donde D es la velocidad de dilución)
3.- Un bio-reactor continuo de una etapa para la producción de células es operado en estado
estacionario.
a)
Demuestre analíticamente que para un bio-reactor de volumen V1 la concentración
celular, en estado estacionario, es mayor que para un bio-reactor de volumen V2 (donde V1 > V2).
b)
Con la idea de maximizar la producción de células, ¿comó operaría dos bio-reactores
continuos de volumen V, en serie o en paralelo?, justifique su respuesta con un ejemplo
cuantitativo.
4. Estudios realizados en el laboratorio mostraron que el cultivo continuo de Azotobacter
winelandi presenta una velocidad específica de crecimiento máxima de 0,45 h-1 y un Ks de 28
mg/L. Si se opera un bio-reactor de 50 L, con una velocidad de dilución de 0,32 h-1, Yx/s = 0,36
g/g y una concentración de sustrato en la alimentación de 5 g/l; determinar:
a)
b)
Concentración celular en estado estacionario.
Concentración de sustrato limitante en el efluente.
SAM/RS
2
5.- En un cultivo por lotes alimentados (C.L.A.) se obtuvieron los siguientes resultados:
Tiempo (h)
0
1
2
3
4
5
6
7
8
9
XV (g)
210
277
364
479
631
831
1.095
1.442
1.898
2.500
Las características de la bacteria cultivada son M = 0.4 h-1, y Ks = 0.01 g/l (para el nutriente
limitante utilizado).
a) Determine el tipo de alimentación usado sabiendo que SF (concentración de sustrato en la
alimentación) es constante.
b) Calcule las condiciones iniciales de concentración de sustrato y célula si el volumen inicial era
de 140 L.
6. Una nueva cepa de levadura está siendo considerada para la producción de biomasa. Para
caracterizar la cepa de levadura se realizaron experimentos en un bio-reactor de una etapa. En la
experimentación se utilizó una concentración de sustrato en la alimentación del bio-reactor de
800 [mg/L], operándose con exceso de oxígeno, pH de 5,5 y una temperatura de 35 [°C]. Los
resultados obtenidos en la experimentación se presentan en la siguiente tabla:
D
[1/h]
0,1
0,2
0,3
0,4
0,5
0,6
0,7
S
[mg/L]
16,7
33,5
59,4
101
169
298
702
X
[mg/L]
366
407
408
404
371
299
59
a)
¿Cuáles son los valores de µmax y Ks?
b)
Encuentre una expresión para la productividad celular DX.
c)
¿Cuál es la velocidad de dilución (D) que maximiza la productividad celular? Compare el
valor teórico con el que se obtiene de la gráfica.
SAM/RS
3
7. Los siguientes datos fueron obtenidos en la oxidación de pesticidas presentes en agua residual.
Los datos fueron obtenidos mediante una mezcla de microorganismos en una operación continua
en una laguna de aireación (tipo quimiostato) donde el pesticida es el reactivo limitante.
D
[1/h]
0,08
0,11
0,24
0,39
0,52
0,70
0,82
[S] (Pesticida)
[mg/L]
15
25
50
100
140
180
240
Si usted tiene un residuo líquido a tratar de 0,5 [m3/s] que contiene 500 [mg/L] de pesticida y
requiere reducir la concentración del pesticida en un 95%:
a)
¿Cuál debe ser la tasa de dilución y el volumen de la laguna de aireación?
b)
¿Cuál es la masa microbiana [Ton] producida por día de operación? Considere que YX/S es
0,6 [g/g]
8. La tasa de crecimiento específico para un microorganismo cultivado en un quimiostato,
satisface la siguiente expresión:

mS
KS  S 
IKS
KI
¿De qué tipo de inhibición se trata?
Para los siguientes valores:
S0 = 10 [g/L]
KS = 1 [g/L]
YX/S = 0,1 [gcel/ gsust]
x0 = 0 [g/L]
KI = 0,01 [g/L]
μm = 0,5 [1/h]
a)
Determine x y S como función de D para I = 0 [g/L]
b)
Cuando se agrega inhibidor al quimiostato (I = 0,05 [g/L]), determine la concentración de
S de salida del sistema y la concentración de células como función de D.
c)
Determine la productividad celular en función de D.
d)
Analice el efecto del inhibidor en dx/dt.
e)
¿Cuál será el volumen del reactor, si éste debe procesar un flujo de 570 [L/h] a la máxima
productividad celular?
SAM/RS
4
9. Los siguientes datos fueron obtenidos para evaluar el efecto de la temperatura en la producción
fermentativa de ácido láctico, mediante el uso de Lactobacillus delbrueckii. De estos datos estime
los parámetros de Arrhenius para el sistema descrito:
T
[°C]
40,4
36,8
33,1
30,0
25,1
μ
[1/h]
0,0140
0,0112
0,0074
0,0051
0,0036
10. La bacteria Pseudomona sp. tiene una tasa máxima específica de crecimiento de 0,4 [1/h],
cuando es cultivada en acetato. La constante de saturación usando este sustrato es 1,3 [g/L], y el
coeficiente de rendimiento de células en acetato es de 0,46 [g cell/ g acetato]. Si se opera este
sistema como un quimiostato, con un S0 de 38 [g/L], realice el siguiente análisis:
a)
b)
c)
d)
e)
¿Cuál es la tasa de dilución crítica?
¿Cuál es la concentración de células cuando la tasa de dilución es la mitad de la crítica?
¿Cuál es la concentración de sustrato cuando la D es un 80% de la crítica?
¿Cuál es la productividad celular a la D en c)?
Encuentre Dópt para la productividad celular, ¿qué porcentaje de Dcrítico es éste?
11. En un quimiostato en que la cinética de crecimiento celular obedece la ecuación de Monod, el
sustrato residual es independiente de la concentración de sustrato inicial o de ingreso al
quimiostato (S0). Usted observa que en su quimiostato, un incremento en S0 resulta en un
incremento en la concentración de salida o residual. Un amigo le sugiere que considere la
ecuación de Contois en lugar de Monod:

mS
K XS X  S
a)
Derive una expresión para S en términos de D, μm, KXS y X para un quimiostato en estado
estacionario.
b)
Derive un expresión para S en función de S0, D, KXS, YXS y μm.
c)
¿Si S0 aumenta al doble, en cuánto aumenta S?
12. Se tiene un fermentador operando en cultivo por lotes alimentado, donde la tasa específica de
crecimiento celular se describe mediante la ecuación de Monod. Se tiene como objetivo
conseguir 600 [Kg] de células secas. Se pide para las siguientes condiciones:
SAM/RS
5
Sf = 90 [g/L] constante
KS = 0,055 [g/L]
YX/S = 0,44 [gcel/ gsust]
X0 = 6 [g/L]
μm = 0,46 [1/h]
μ = 0,33 [1/h] constante
V0 = 10.000 [L]
a)
Expresión para el flujo de alimentación F en el tiempo, en función de las variables
anteriores.
b)
Tiempo de alimentación [h]
c)
Concentración de nutrientes limitantes en la alimentación [g/L]
d)
Volumen final en el fermentador [L]
e)
Valor de F a t = 0 [h]
f)
El valor del flujo a la mitad del tiempo del proceso [L/h]
RESPUESTAS (con desarrollo)
1. a) Unicellular organisms (e.g. bacteria) duplicate in a process called cell division. Each cell
divides into two new cells within a certain time, called generation time (tg). Schematically, we
can represent this division process as depicted in the following Figure:
Therefore, if we have N0 bacteria at time = 0, then after 1 generation (1tg) we will have 2N0
bacteria, and after 2 generations (2tg) we will have 4N0 bacteria, and so on, implying that after
SAM/RS
6
each generation time, the bacterial population is duplicating. Putting this information in a table,
we get:
Time
0
1tg
2tg
3tg
…
…
ntg
Bacteria population
N0 = 20N0
2N0 = 21N0
4N0 = 22N0
8N0 = 23N0
…
…
N = 2n N 0
In addition, the number of generations (n) is related to time (t) and generation time (tg) as
follows:
n=
t
(for t = 0, n = 0; for t = 1tg, n = 1, and so on)
tg
Then replacing n from Equation in the expression N = 2nN0, we get:
t
tg
N = 2 N0
Now arranging the previous Equation 9.9, we can obtain:
 N
ln 
 N0
 t
  ln 2
 tg
By definition, ln2/tg = µ (specific growth rate), thus the number of bacteria after time t can be
expressed by the exponential equation as follows:
N = N0 e μt
b) tD = (Ln2)/
2. De un balance de células se obtiene:
(2)
Dado que el sistema está en estado estacionario y, además x0 = 0, entonces:
(3)
De la ecuación 3 se obtiene: F/V = , y por definición F/V = D, entonces:
D
SAM/RS
7
3. a) De la expresión:
x  y x / s ( S0 
DKS
)
max .  D
x  y x / s ( S0 
Considerando que D = F/V, entonces:
FK S
)
V max .  F
Donde es posible apreciar que a mayor V, mayor es la concentración celular, x. Por lo tanto si V1
> V2, entonces X1 > X2.
b) Es mejor en serie que en paralelo. No olvide desarrollar un ejemplo numérico. Si asumimos
que el flujo de alimentación es F y se opera en serie la productividad la productividad será Fx2.
Al operar en paralelo será Fx1. Se puede demostrar que x2 > x1.
4. a) x = 1,775 g/L; b) S = 68,92 mg/L
5. a) Alimentación exponencial (note que al graficar XV versus el tiempo se comprueba que es
una función exponencial).
b) xo = 1,5 g/L ; So = 0,022 g/L
6. a) Para el quimiostato, la tasa específica de crecimiento celular puede ser expresada por la
ecuación de Monod:

m S 
K S  S 
(1)
Sin embargo, en estado estacionario, el flujo de células que salen del quimiostato, también
conocido como tasa de dilución, puesto que se asume mezclado perfecto en el reactor es igual a la
tasa de crecimiento específica en éste, es decir, D = μ, por lo que la ecuación de Monod puede ser
re-escrita como:
D
 m S 
K S  S 
(2)
A partir de los valores entregados en la tabla, se puede determinar μmáx y KS mediante regresión
no lineal o por regresión lineal al graficar los inversos de D y [S].

Regresión no lineal:
 1
m  0,8  
h 
 mg 
K S  102,3 

 L 
SAM/RS
8

Regresión lineal:
12,00
10,00
1 KS 1
1


D m S  m
1/D
8,00
6,00
4,00
1/D
[h]
10,00
5,00
3,33
2,50
2,00
1,67
1,43
2,00
1/[S]
[L/mg]
0,060
0,030
0,017
0,010
0,006
0,003
0,001
0,00
0,000
0,010
0,020
0,030
0,040
0,050
0,060
0,070
1/[S]
De la ecuación de la recta se extrae el intercepto y de aquí la velocidad máxima. Luego con la
pendiente y μmáx se obtiene KS:
m
 1
 1,25  m  0,8  
h
KS

1
m
K
5,00  2,00
 mg 
 125,3  S  KS  100,3 

0,030  0,006
0,8
 L 
b) Se define productividad celular como: DX
Tomando las ecuaciones que describen el comportamiento del quimiostato:
X  YX /S S0  S 
S  
KS D
m  D
(3)
(reordenando la ecuación (2))
(4)
Luego, multiplicando la ecuación (3) por D y reemplazando la ecuación (4) en ésta, se obtiene
una expresión para la productividad celular DX:
X  YX /S S0  S 
DX  DYX /S S0  S 

K D 
DX  DYX /S  S0  S 


m D
(5)
c)
Para obtener la tasa de dilución teórica que maximiza la productividad celular (Dóptimo), se
deriva la ecuación (5) en función de D, se iguala a cero y se despeja Dóptimo:
d  DX 
dD
SAM/RS


KS D  
KS
d 
 DYX /S  S0 
   0  Dóptimo  m  m
dD 
m  D  
S0  KS

9

KS
 1
 1,07  
Dóptimo,1  m  m
S0  K S
 h  (se


KS
 1

Dóptimo,2  m  m S  K  0,53  h 
0
S

descarta)
Si se observa la gráfica que representa el comportamiento del quimiostato:
[S]
[mg/L]
16,7
33,5
59,4
101
169
298
702
[X]
[mg/L]
366
407
408
404
371
299
59
D[X]
[mg/L h]
36,6
81,4
122,4
161,6
185,5
179,4
41,3
900
800
700
Concentración
D
[1/h]
0,1
0,2
0,3
0,4
0,5
0,6
0,7
600
[S]
500
D[X]
400
[X]
300
Dcrit
200
S0
100
Dópt
0
0
0,2
0,4
0,6
0,8
Ahora, Dóptimo, se extrae desde la gráfica siendo su valor igual a ~ 0,56
[1/h].
D
Finalmente, se puede decir que los valores encontrados son casi iguales, siendo la principal causa
de diferencia el error respectivo de valores obtenidos experimentalmente y la gráfica de éstos.
7.
a) Análogo al ejercicio 6, se grafica los inversos y se obtiene los parámetros para la relación
del quimiostato en estado estacionario:
14,00
1 KS 1
1


D m S  m
1/[S]
[L/mg]
0,067
0,040
0,020
0,010
0,007
0,006
0,004
10,00
1/D
1/D
[h]
12,50
9,09
4,17
2,56
1,92
1,43
1,22
y = 186,5x + 0,606
R² = 0,987
12,00
8,00
6,00
4,00
2,00
0,00
0,000
0,010
0,020
0,030
0,040
0,050
0,060
0,070
1/[S]

 1
 0,606  m  1,65  

m
KS D
h
307,8D


S 
m  D 1,65  D
KS
K
 mg  
 186,5  S  KS  307,8 

m
1,65
L


1
Se quiere abatir la concentración en un 95%
SAM/RS

(1)
S0  S
 mg 
 0,95  S  25 

S0
 L 
10
Se reemplaza dicho valor en la ecuación (1) y se despeja la tasa de dilución:
S  25 
307,8D
 1
 D  0,12  
1,65  D
h
Finalmente se despeja el volumen a partir de la definición de tasa de dilución:
D
 m3 
F
F
s  1
 V   0,5    3600   
h
V
D
 h  0,12
 s 
 V  15.000 m3 
b) Se determina la masa microbiana utilizando el coeficiente de rendimiento:
 mgcélulas 
 mgsustrato 
 mgcélulas 
X  YX /S S0  S   0,6 
 285 
   500  25  


L
L




 mgsustrato 
 m3 
 mgcélulas 
 s 
 L  1
Masamicrobiana  285 

0,5
 1000  3   9

  3600  24 


 día 
 m  10
 L

 s 
Toncélulas 


 mgcélulas 
Ton 
Masamicrobiana  12,3 

 día 
8. Por la forma de la expresión que describe la tasa específica de crecimiento celular, se deduce
que es una inhibición del tipo competitiva.
a) Para determinar S en función de D, se realiza el balance de células para el quimiostato:
Acumula  Entra  Sale  Genera
d  XV 
dt


Dado que x0 = 0 [g/L],
 FX 0  FX   XV
dX
dt
dX
dt

F
 X0  X    X  D  X0  X    X
V
 DX   X  X    D 
Asumiendo estado estacionario  d  X   0  X    D     D
dt
, pero V  cte
(1)
X 0
Si [I] = 0 [g/L], entonces la tasa específica de crecimiento celular puede ser representada por la
ecuación de Monod:

SAM/RS
mS
KS  S
11
Pero   D ,
Reordenando, se tiene:
 D
mS
KS  S
S
(2)
DKS
(3)
m  D
Reemplazando los parámetros del enunciado en la ecuación (3), se obtiene:
S
D
0,5  D
(4)
Ahora, para determinar X en función de D, se realiza el balance de materia para el sustrato:
Acumula  Entra  Sale  Consume
d SV 
 FS0  FS 
dt

d S 
dt

X
V
YX /S
, pero V  cte
F
X
X
 D S0  S  
S0  S  
V
YX /S
YX /S
(5)
Introduciendo la ecuación (1) en (5):
d S 
dt
 D S0  S  
DX
YX /S
Asumiendo nuevamente estado estacionario y considerando que:
dX
dS

0
dt
dt

d S 
dt
 0  D S0  S  

DX
X 
 D  S0  S  

YX /S D 0 
YX /S 
 X  YX /S S0  S  (6)
Reemplazando los parámetros del enunciado y la ecuación (4) en la ecuación (6), se
obtiene:
D 

X  0,1 10 
0,5
 D 

(7)
b) Como se está trabajando en estado estacionario, los balances de materia anteriores son
válidos. Sin embargo, varía la definición de la tasa específica de crecimiento celular
puesto que esta vez existe inhibidor, por lo que la ecuación (2) se escribe de la siguiente
manera:
 D
SAM/RS
mS
IK
KS  S  S
KI

mS

I 
KS  1    S
 KI 
(8)
12
Reordenando la ecuación (8) para despejar S:

I 
KS  1   D
 KI 
S
m  D
(9)
,y reemplazando los parámetros del enunciado en la ecuación (9) se tiene:
 0,05 
1 1 
D
0,01 
S 
0,5  D
S
6D
0,5  D
(10)
Finalmente, sustituyendo la ecuación (10) y los valores de S0 e YX/S en la ecuación (6) se
obtiene la expresión para x:
6D 

X  0,1 10 
0,5  D 

(11)
c) Se define la productividad celular como:
(12)
DX
Por lo que multiplicando la ecuación (11) por la tasa de dilución, se consigue una
expresión para ésta:
6D 

DX  0,1D  10 
0,5  D 

d) Se define la variación de la concentración de células en el tiempo como:
dX
 X
dt
(13)
Dado que para el quimiostato operando en estado estacionario se cumple que   D , la
ecuación (13) se transforma en:
dX
 DX
dt
es decir, la variación de la concentración de células en el tiempo es equivalente a la
productividad celular.
Si se hace una comparación para dx/dt con y sin inhibidor:
SAM/RS
13
dX
6D 

 0,1D  10 
dt
0,5  D 

dX
D 

 0,1D  10 
dt
0,5  D 

I   0
I   0
Se aprecia que cuando existe inhibidor, será menor la variación de células en el tiempo
puesto que el coeficiente que acompaña a la tasa de dilución (6 > 1) es mayor.
e) Si se observa una gráfica representativa (nota: valores de los ejes no están relacionados
con el ejercicio) de productividad celular en función de la tasa de dilución:
250
DX máx
200
DX
150
100
50
0
0
0,1
0,2
0,3
0,4
0,5
D
0,6
0,7
0,8
Dópt Dcrít
se puede concluir que para obtener la productividad máxima se debe operar a la tasa de
dilución óptima, por lo que se derivará la función de productividad e igualará a cero para
obtener su máximo:
6D 
0,6D

DX  0,1D 10 
  D  0,5  D
0,5

D


 0,6D  0,6D 2 
d  DX 

 1 

2
dD
  0,5  D  

d  DX 
dD
 0  1,6D2  1,6D  0,25  0
(14)
De la ecuación (14) se obtienen dos posibles valores para la tasa de dilución óptima:

D1  0,194 1/ h 


D2  0,806 1/ h 
Para establecer cuál de estos valores es el adecuado, se determinará la tasa de dilución
crítica (Dcrít) que es el valor de D cuando la productividad y la concentración de células es
cero. También, Dcrít corresponde a la tasa de dilución donde la concentración de sustrato
es la de entrada o inicial (S0):
Dcrít  D S 
0
mS0
IK
KS  S0  S
KI

0,5  10
0,05  1
1  10 
0,01
 1
 Dcrít  0,31 
h
SAM/RS
14
Dado que Dópt  Dcrít (véase gráfico representativo)  Dópt  0,194  1 
 
h
Finalmente, se despeja el volumen del reactor desde la tasa de dilución:
D
F
F
1
L 
 V   570   
h
V
D
h
0,194
 
 V  2938 L
9. La ecuación de Arrhenius viene descrita por:
  k0 e

Ea
RT
(1)
Por lo que, para determinar sus parámetros, una manera práctica es linealizar los datos
entregados mediante la siguiente expresión, obtenida luego de aplicar logaritmo natural a la
ecuación (1):
Ln     Ln  k0  
Ea 1
R T
(2)
Se tiene entonces la siguiente gráfica:
1/T
[1/K]
0,00319
0,00323
0,00327
0,00330
0,00335
Ln(μ)
--4,27
-4,49
-4,91
-5,28
-5,63
-4,00
0,00315
-4,20
0,00320
0,00325
0,00330
0,00335
0,00340
-4,40
-4,60
-4,80
Ln(μ)
T
[K]
313,6
310,0
306,3
303,2
298,3
-5,00
-5,20
y = -8715,x + 23,55
R² = 0,988
-5,40
-5,60
-5,80
-6,00
1/T
 Ea
Ea
 J 
 R  8,314  8715  Ea  72457  mol 


Finalmente, 

1
Ln  k   23,5  k  e 23,5  
0
0
h 

 
Nota: Obtenga los parámetros k0 y Ea a través de una regresión no lineal y compare.
SAM/RS
15
10.
a) Como ya se ha demostrado, para un quimiostato operando en estado estacionario, la tasa
de dilución crítica viene dada por:
D
m S
KS  S
 Dcrítico 
mS0
KS  S0

0,4  38
1,3  38
 1
 Dcrítico  0,39  
h
b) Para determinar la concentración de células, primero se determina la concentración de
sustrato para la tasa de dilución especificada y luego este valor se reemplaza en la
definición de concentración de células a partir del coeficiente de rendimiento.
Dcrítico 0,39
 1

 0,19  
2
2
h
DKS
0,19  1,3
g 
S 

 1,2  
m  D 0,4  0,19
L 
D
 X  YX /S  S0  S   0,46   38  1,2 
g

 X  17  células 
 L 
c) Se calcula la concentración de sustrato análogamente a la alternativa anterior:
 1
D  0,8Dcrítico  0,8  0,39  0,31 
h
DKS
0,31 1,3
g 
S 

 4,4  
m  D 0,4  0,31
L 
d) Para obtener la productividad celular, se establece la concentración de células y
posteriormente se multiplica este valor por la tasa de dilución:
g

X  YX /S S0  S   0,46   38  4,4   15,4  células 
L


 DX  0,31 15,4
g

 DX  4,8  células 
L

h


e) Como ya se vio, la tasa de dilución óptima se puede definir como:
Dóptimo  m  m
KS
1,3
 0,4  0,4
S0  KS
38  1,3
 1
 Dóptimo  0,33  
h
, y el porcentaje es:
SAM/RS
16
Dóptimo

Dcrítico
0,33
 100  84,6%
0,39
11.
a) Análogo al procedimiento descrito en el ejercicio 3, para determinar S se realiza un
balance de materia para la concentración de células:
Acumula  Entra  Sale  Genera
d  XV 
dt

Asumiendo que x0 = 0,
 FX 0  FX   XV
dX
dt
dX

dt

, pero V  cte
F
 X0  X    X  D  X0  X    X
V
 DX   X  X    D 
, y dado que se opera en estado estacionario  d  X   0  X    D     D
dt
(1)
X 0
Por lo que, se puede despejar S mediante el reordenamiento de la ecuación de Contois
combinada con la ecuación (1):
 D
mS
K XS X  S
 S  DK XS X
(2)
m  D
b) Se desarrolla el balance de materia para el sustrato, para obtener una expresión para X y
así obtener S sin que dependa de x:
Acumula  Entra  Sale  Consume
d SV 
X
, pero V  cte
 FS0  FS 
V
dt
YX /S

d S 
dt

F
X
X
 D S0  S  
S0  S  
V
YX /S
YX /S
(3)
Introduciendo la ecuación (1) en (3):
d S 
dt
 D S0  S  
DX
YX /S
Asumiendo estado estacionario y considerando que:
dX
dS

0
dt
dt

SAM/RS
d S 
dt
 0  D S0  S  

DX
X 
 D  S0  S  

YX /S D 0 
YX /S 
17
 X  YX /S S0  S 
(4)
Reemplazando la ecuación (4) en la ecuación (2):
S 
Sea R  DK XSYX /S ,
DK XSYX /S S0  S 
m  D
RS0
RS
S 

m  D m  D

RS0
R 
 S 1 



D


m

m D

R


  D 

S  S0  m
1  R 

m  D 
(5)
c) A partir de la ecuación (5), si se define un nuevo parámetro R’ como:
R


  D 

R'   m
1  RS 
 m  D 
La concentración de sustrato queda descrita por:
S  S0R '
Donde se aprecia claramente que si S0 se duplica, S también lo hace.
t
12. a) F   X 0V0e
YX /S  Sf  S 
b)
c)
d)
e)
f)
t = 7,0 [h]
S = 0,14 [g/L]
V = 23.658 [L]
F0 = 501 [L/h]
F = 1.584 [L/h]
SAM/RS
18
EJERCICIOS PROPUESTOS
1. Un biorreactor continuo se opera con un volumen de trabajo de 120 L y un flujo de
alimentación de 20 L/h. La población bacteriana presenta un tiempo de duplicación mínimo
de 3,15067 h y un Ks de 1 g/L. El rendimiento expresado en g de células por g de sustrato se
ha estimado en 0,28. Ensayos preliminares hacen recomendable trabajar a una velocidad de
dilución igual al 82% del valor crítico*.
* Velocidad de dilución crítica, D*= MSo/(So + Ks)
So : Concentración de sustrato en la alimentación (g/L)
M : Velocidad específica máxima (h-1)
Recuerde:  = Ln2/tD, donde tD es el tiempo de duplicación.
a)
b)
c)
d)
e)
¿Cuál es la velocidad específica máxima, M?
¿Cuál es la concentración de sustrato en la alimentación?
¿Cuál es la concentración de sustrato en la descarga?
¿Cuál es la concentración celular en estado estacionario?
¿Cómo cambian las respuestas b) y c) si el flujo de alimentación se disminuye a 15 L/h?
2. Formule los balances de células y sustrato en estado no estacionario para el esquema que se
presenta en la siguiente figura.
3. Un bio-reactor del tipo Fed Batch (cultivo por lotes alimentados) se opera de tal forma que la
concentración de sustrato se mantenga constante durante la operación (S*= 2 g/L).
Datos:
S0=20 (g/L); X0= 2 (g/L); V0=2000 (L); =0,4 (h-1); YX/S=0,4 (g/g)
SAM/RS
19
a) ¿Cuál es la concentración de células después de 4 horas de fermentación?
b) ¿Cuál es el volumen de fermentación después de 4 horas de operación?
c) Si se realizara una fermentación batch (por lotes) con la misma concentración
inicial, ¿cuál sería la concentración después de 4 horas de fermentación?
d) Compare sus respuestas a las preguntas formuladas en las letras a) y c) y explique las
diferencias.
4.
a) Formule los balances de células y sustrato en estado estacionario para el esquema que se
presenta en la siguiente figura.
b) Si S0=20 (g/L), M=4 (h-1); KS=0,5 (g/L); D=0,2 (h-1); YX/S=0,5 (g/g), entonces calcule las
condiciones de estado estacionario para el primer bio-reactor, es decir: X1, S1, y 1, y deje
expresadas las ecuaciones que permitan calcular X2, S2, y 2
F
S0
I
II
V, X1, S1
V, X2, S2
F
X1
F
X2
S2
S1
5. Un bio-reactor continuo de dos etapas se opera con un volumen de trabajo de 10 L (cada etapa) y un
flujo de alimentación de 4 L/h con una concentración de sustrato de 22 g/L en la primera etapa. La
población bacteriana presenta una velocidad específica de crecimiento máxima de 0,6 h-1 y un Ks de 1 g/L.
El rendimiento expresado en gramos de células por gramo de sustrato consumido se ha estimado
experimentalmente en 0,5 g célula/g sustrato.
a) Calcule la concentración de células y sustrato en la descarga de la primera etapa.
b) Calcule la concentración de células y sustrato si se sabe que la velocidad específica de crecimiento en la
segunda etapa del bio-reactor es igual a: 0,035326447 h-1
c) Calcule la concentración de células y sustrato en el caso que los dos bio-reactores se disponen en
paralelo. Considere que el flujo de alimentación a cada bio-reactor es 2 L/h.
d) Compare y comente los resultados obtenidos en b) y c).
6. Un bio-reactor es operado en la modalidad por lotes alimentados. Para la fermentación se ocupará una
cepa microbiana que tiene las siguientes características:
SAM/RS
20
µmáx. = 0,6 h-1
Ks = 8 mg/L
YX/S = 0,5 g. célula/g. sustrato
La concentración de sustrato se mantendrá en 3 g/L durante la operación del cultivo por lotes alimentado.
Por lo tanto se ha optado por tener un flujo de alimentación exponencial y una concentración de sustrato
constante en la alimentación e igual a 23 g/L. Para efectos prácticos se puede considerar que µ = µmáx. si µ
> 0,99 µmáx. El volumen inicial es de 2000 L y la concentración inicial de células es de 2 g/L. Después de
6 h, desafortunadamente, se produce un desperfecto y se corta el flujo de alimentación. Ud como jefe de
planta decide que la fermentación continúe en modalidad batch hasta que la concentración de sustrato (que
es constantemente medida) sea igual a 1 g/L.
a) ¿Cuál era la masa celular en el bio-reactor a las 6 horas de operación?
b) ¿Cuál era el volumen de fermentación a las 6 horas de operación?
c) ¿Cuál era la concentración de células a las 6 horas de operación?
d) ¿Por cuánto tiempo se prolongó la fermentación batch?
e) ¿Cuál era la concentración de células al término de la fermentación batch?
f) ¿Hasta qué concentración de sustrato se podría llegar de tal forma que todavía las células sigan
creciendo a µmáx.?
7. A un bio-reactor continuo de una etapa se ha acoplado un sedimentador tal como se muestra en la figura
siguiente. La corriente de recirculación está concentrada en células y no contiene sustrato.
Datos:
µmáx. = 2 h-1, Ks = 1000 ppm, YX/S = 0,5 g. célula/g. sustrato, F = 100 L/h, S2 = 0,5 g/L, S0 = 3 g/L, X0 = 0, ρ
= 1 kg/L
a) Calcule la concentración de células y sustrato en la descarga del bio-reactor.
b) Calcule el volumen de bio-reactor.
8. Para un sistema de tratamiento de aguas residuales se ha propuesto el siguiente sistema.
SAM/RS
21
a) Formule los balances de células y sustrato en el bio-reactor y, también en el sedimentador.
b) Sí F = 310.000 m3/día; F2 = 6.700 m3/día; V = 68.000 m3; α = 0,197; x = 21000 células/ml y
x1 = 52 células/ml, calcule µ.
9. Un bio-reactor continuo de dos etapas se opera con un volumen de trabajo de 10 L (cada etapa) y un
flujo de alimentación de 4.5 L/h con una concentración de sustrato de 20 g/L en la primera etapa. La
población bacteriana presenta una velocidad específica de crecimiento máxima de 0,5 h-1 y un Ks de 1 g/L.
El rendimiento expresado en gramos de células por gramo de sustrato consumido se ha estimado
experimentalmente en 0,4 g célula/g sustrato.
a) Calcule la concentración de células y sustrato en la descarga de la primera etapa.
b) Calcule la concentración de células y sustrato si se sabe que la velocidad específica de crecimiento en la
segunda etapa del bio-reactor es igual a: 0,194371 h-1
c) Calcule la concentración de células y sustrato en el caso que los dos bio-reactores se disponen en
paralelo. Considere que el flujo de alimentación a cada bio-reactor es 2,25 L/h.
d) Compare y comente los resultados obtenidos en b) y c)
10. Un bio-reactor es operado en la modalidad por lotes alimentados. Para la fermentación se ocupará una
cepa microbiana que tiene las siguientes características:
µmáx. = 0,4 h-1
Ks = 5 mg/L
YX/S = 0,4 g. célula/g. sustrato
La concentración de sustrato se mantendrá en 2 g/L durante la operación del cultivo por lotes alimentado.
Por lo tanto se ha optado por tener un flujo de alimentación exponencial y una concentración de sustrato
constante en la alimentación e igual a 22 g/L. Para efectos prácticos se puede considerar que µ = µmáx. si µ
> 0,99 µmáx. El volumen inicial es de 2000 L y la concentración inicial de células es de 2 g/L. Después de
5 h, desafortunadamente, se produce un desperfecto y se corta el flujo de alimentación. Ud como jefe de
SAM/RS
22
planta decide que la fermentación continúe en modalidad batch hasta que la concentración de sustrato (que
es constantemente medida) sea igual a 1 g/L.
a) ¿Cuál era la masa celular en el bio-reactor a las 5 horas de operación?
b) ¿Cuál era el volumen de fermentación a las 5 horas de operación?
c) ¿Cuál era la concentración de células a las 5 horas de operación?
d) ¿Por cuánto tiempo se prolongó la fermentación batch?
e) ¿Cuál era la concentración de células al término de la fermentación batch?
f) ¿Hasta qué concentración de sustrato se podría llegar de tal forma que todavía las células sigan
creciendo a µmáx.?
11. Para realizar una fermentación industrial se dispone de un sistema de bio-reactores multietapa tal como se muestra en la figura adjunta. En la primera etapa se alimenta un flujo de 32 L/h
y con una concentración de sustrato de 35 g/L. Entre las dos etapas, se agrega una alimentación
adicional, con un flujo de 12 L/h y una concentración de sustrato de 25 g/L.
Determine cuáles son las condiciones de salida en la segunda etapa (F2, S2, x2 y 2)
F0
S0
x0
F2
S2
x2
F0 S1 x1
Datos:
V = 80 L
M = 0.57 h-1

V
1
F1
S01
KS = 0.09 g/L

V
Yx/S = 0.43 g/g
2
R:
SAM/RS
23
12. De los datos obtenidos en un proceso batch (por lotes), se determinó que el crecimiento viene
descrito por el Modelo de Monod, con valores de los parámetros de max = 0.7 h-1 ; Ks = 1.5 g/L y
Yx/s = 0,12 g/g. Se desea llevar a cabo el mismo crecimiento a escala industrial en un bio-reactor
continuo (mezcla perfecta).
a) Suponiendo que la alimentación es estéril (x0 = 0), ¿Cuál será el volumen de fermentador
necesario para tratar un caudal de 300 L/h, con una concentración de sustrato de 20 g/L si
se desea convertir un 90% del sustrato alimentado?
b) ¿Cuál será la producción de biomasa?
c) Con el fin de aumentar el caudal a tratar, se propone utilizar el mismo reactor con
recirculación. Mediante un sistema de filtración, se obtiene una corriente de recirculación
con una concentración celular que es cuatro veces la de salida del bio-reactor. Si se desea
obtener la misma conversión global del 90% para el sustrato, trabajando a una relación de
recirculación (caudal de recirculación/caudal de alimentación) de 0.25, ¿Cuál será el
caudal de entrada que podrá ser tratado? ¿Cuál será la producción de biomasa en esas
condiciones?
R:
SAM/RS
24
13. Se lleva a cabo un cultivo por lotes seguido por un cultivo por lotes alimentados para la
producción de biomasa, con alimentación exponencial. El volumen inicial de fermentación es de
10 l, la concentración inicial de células es de 0.2 g/l, la concentración inicial de sustrato es 12 g/l,
el rendimiento de sustrato es de 0.46 g/g, la velocidad específica máxima de crecimiento es
0.4 h-1, Ks = 10 mg/l y la concentración de sustrato en la alimentación es de 100 g/l.
Calcular:
a)
El tiempo al que se inicia la alimentación, si en cultivo por lotes alimentados se desea
mantener una concentración de sustrato de 0.8 g/l.
b) El flujo inicial del cultivo por lotes alimentados.
c) El tiempo total de fermentación (batch + C.L.A) y la concentración celular al momento
de alcanzar un volumen de 20 l.
R:
SAM/RS
25
14. Ud. dispone de 2 bio-reactores a nivel de planta piloto con volúmenes de 100 y 200 L
respectivamente para la producción de células. El caldo estéril a tratar tiene un flujo volumétrico
de 50 L/h con una concentración de sustrato de 5 g/L. Experimentos a nivel de laboratorio
indican que el micro-organismo tiene una velocidad específica máxima de 0,8 h-1 y un Ks = 1
g/L. El rendimiento de sustrato (Yx/s) es de 0,5 g/g. Ud. a decidido operar los bio-reactores en
modo continuo y en serie.
a) Si se desea maximizar la concentración de células en la descarga del segundo bio-reactor,
¿cuál de los dos bio-reactores pondría primero?
b) Si se desea optimizar la operación con estos dos bio-reactores, ¿qué flujo volumétrico
utilizaría?
R:
SAM/RS
26
15. En el manuscrito: “Production of Ethanol by Fed-Batch Fermentation” se presenta el
siguiente balance de células:
dx
F
 x  x
dt
V
a) ¿Es correcto este balance de células?, Justifique con ecuaciones
R: Si, es correcto y se obtiene de combinar el balance global y el de células.
Balance Global
F
dV
dt
(1)
Balance de Células
xV 
d ( xV )
dt
xV  x
(2)
dV
dx
V
dt
dt
(3)
Remplazando (1) en (3)
xV  xF  V
dx
dt
Dividiendo por V y despejando:
x  x
F dx

V dt
SAM/RS
27