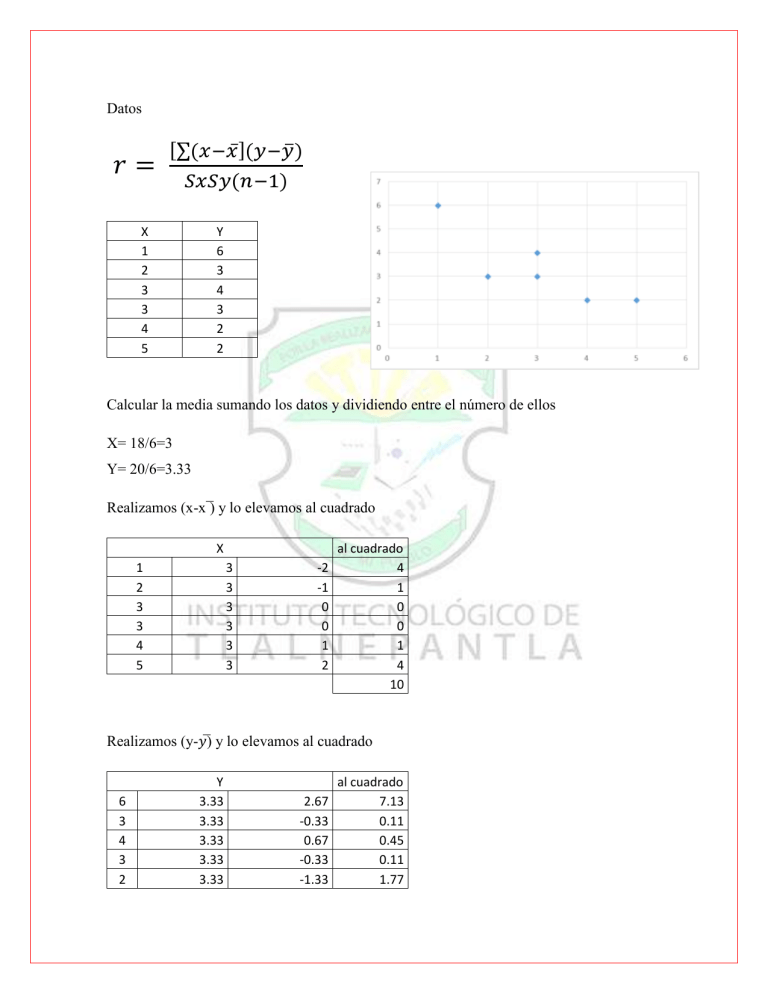
Datos 𝑟= [∑(𝑥−𝑥̅ ](𝑦−𝑦̅) 𝑆𝑥𝑆𝑦(𝑛−1) X 1 2 3 3 4 5 Y 6 3 4 3 2 2 Calcular la media sumando los datos y dividiendo entre el número de ellos X= 18/6=3 Y= 20/6=3.33 Realizamos (x-x ̅) y lo elevamos al cuadrado X 1 2 3 3 4 5 3 3 3 3 3 3 -2 -1 0 0 1 2 al cuadrado 4 1 0 0 1 4 10 Realizamos (y-𝑦̅) y lo elevamos al cuadrado 6 3 4 3 2 Y 3.33 3.33 3.33 3.33 3.33 2.67 -0.33 0.67 -0.33 -1.33 al cuadrado 7.13 0.11 0.45 0.11 1.77 2 3.33 -1.33 1.77 11.33 Realizamos (x-x ̅)(y-𝑦̅) Multiplicación -5.34 0.33 0 0 -1.33 -2.66 -9 Realizamos Sx y Sy: 10 𝑆𝑥 = √ = 1.41 5 11.33 𝑆𝑦 = √ = 1.50 5 Sustituimos la fórmula: [∑(𝑥 − ̅̅̅̅̅̅̅̅̅̅̅̅̅ 𝑥)(𝑦 − 𝑦̅)] 𝑟= 𝑆𝑥𝑆𝑦(𝑛 − 1) 𝑟= Prueba de Hipótesis −9 (1.41)(1.50)(5) = −.85 𝑡. 𝑐. = 𝑡. 𝑐. = 𝑟(√𝑛 − 2) √1 − 𝑟 2 −.85(√4) √1 − (−.85)2 = −3.22 V=n-2=4 α=0.05/2=0.025 =2.77 Se acepta Ha Ŷ= a + bx b= r Sy /Sx a= Ŷ-b x Sustituimos 𝑏 = −.85 1.50 = −.90 1.41 𝑎 = (3.33) − (−.9)(3) = 6.03 Para Ŷ sustituimos todos los valores en (x) Ŷ = 6.03 + (−.9)(5) = 5.13 Los resultados los sustituimos en (Y) y graficamos. X 1 2 3 3 4 5 Y 5.13 4.23 3.33 3.33 2.43 1.53