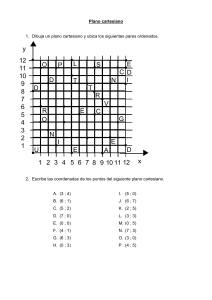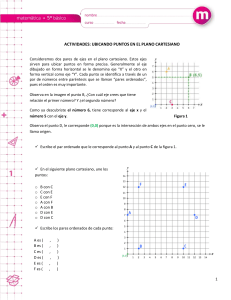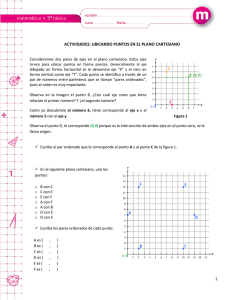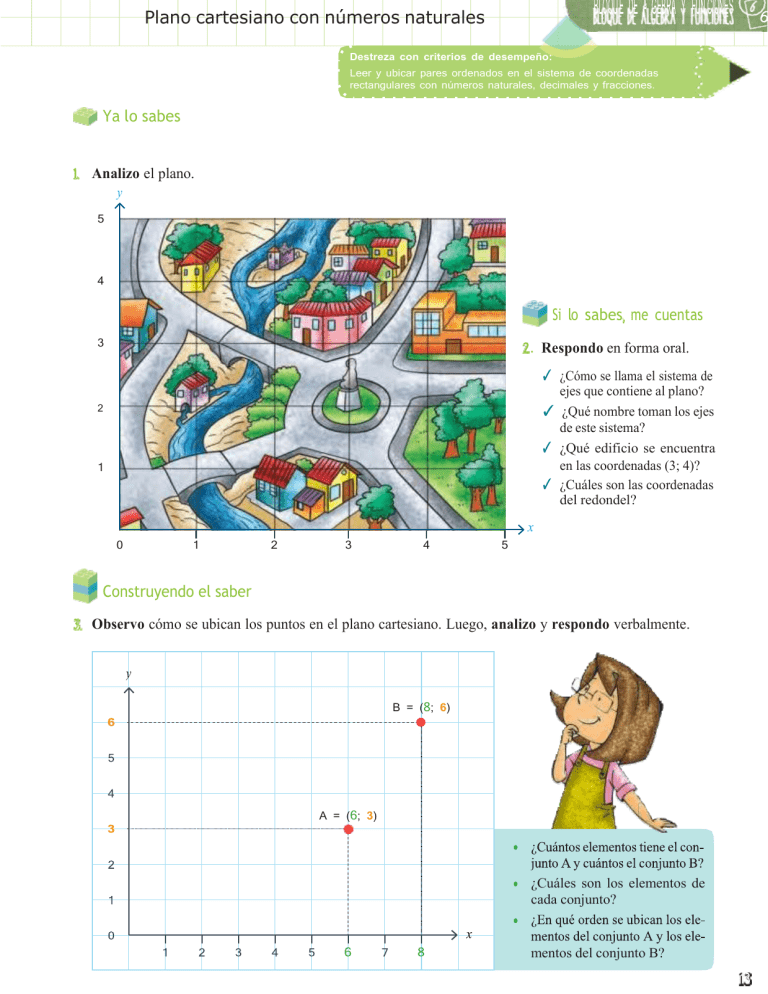
BLOQU E DE ÁLGEBRA Y FUN CIONES Plano cartesiano con números naturales Destreza con criterios de desempeño: Leer y ubicar pares ordenados en el sistema de coordenadas rectangulares con números naturales, decimales y fracciones. Ya lo sabes 1. Analizo el plano. y 5 4 Si lo sabes, me cuentas 3 2. Respondo en forma oral. ✓ ¿Cómo se llama el sistema de ejes que contiene al plano? ✓ ¿Qué nombre toman los ejes de este sistema? ✓ ¿Qué edificio se encuentra en las coordenadas (3; 4)? ✓ ¿Cuáles son las coordenadas del redondel? 2 1 x 0 1 2 3 4 5 Construyendo el saber 3. Observo cómo se ubican los puntos en el plano cartesiano. Luego, analizo y respondo verbalmente. B = (8; 6) A = (6; 3) ¿Cuáles son los elementos de cada conjunto? mentos del conjunto B? 4. Analizo las características que tiene un plano cartesiano con números naturales. Los puntos Representan pares ordenados, (x, y). A x se la conoce como abscisa; a y se la conoce como ordenada, el conjunto se denomina: coordenadas. Se ubican en el plano cartesiano. Están formados por números naturales, se representan con el símbolo ℕ . Los pares ordenados de números naturales se ubican en el primer cuadrante del plano cartesiano, considerando que este tiene 4 cuadrantes. Los números naturales son un subconjunto de los números enteros. Los números naturales se pueden contar y son indefinidos. ℕ = 0,1,2,3,4,... Más ejemplos, más atención 1. Analizo cómo se ubican los puntos A B C D = = = = (5; (2; (3; (1; 2) 5) 1) 7) E = (7; 7) D = (1; 7) E = (7; 7) B = (2; 5) A = (5; 2) C = (3; 1) Estrategia: Identificar datos del gráfico. A= (1; 1) B= (5; 3) C= (7; 7) D= (2; 5) E= (4; 4) digital D = (12; 25) dirección: http://goo.gl/ jPLCV A = (18; 26) B = (11; 20) C = (9; 20) Ciudades Temperatura promedio anual (°C) Pares ordenados Mínima Máxima Esmeraldas 18 26 A = (18; 26) Pastaza 11 20 B = (11; 20) Puyo 9 20 C = (9; 20) San Lorenzo 12 25 D = (12; 25) mínima 10 12 14 16 18 Destreza con criterios de desempeño: Reconocer los elementos de un círculo en representaciones gráficas y calcular la longitud(perímetro) de la circunferencia y el área de un círculo en la resolución de problemas.