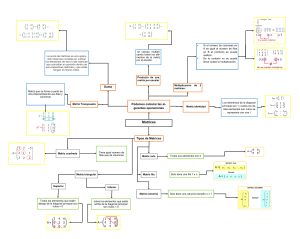
TEMA 2. 2.1 DEFINICIÓN DE MATRÍZ Y PROPIEDADES: Una matriz se define como un arreglo rectangular de números, dispuestos en m renglones es decir; filas y n columnas. El tamaño de una matriz se escribe de la forma mxn, donde m es el número de filas horizontales y n es el número de columnas verticales. Ejemplo: a11 a12 a13 a14 a21 a22 a23 a24 filas a31 a32 a33 a34 a41 a42 a43 a44 columnas PROPIEDADES: 1. SUMA: Las matrices se pueden sumar si solo si ambas poseen el mismo tamaño, es decir; tienen el mismo número de filas y el mismo número de columnas. Se suman componentes con componentes.Ejemplo: 2 4 6 7 3 1 5 4 1 3 2 1 + 4 3 5 5 2+3 4+1 6+5 7+4 2 4 1 7 = 1+2 3+4 2+1 1+7 5 2 1 1 4+5 3+2 5+1 5+1 5 5 11 11 = 3 7 3 8 9 5 6 6 2. RESTA: La resta de matrices consiste en el mismo procedimiento utilizado para sumar, donde ambas matrices deben poseer el mismo tamaño, la única diferencia es utilizar el signo de restar. 3. MULTIPLICACIÓN DE UN ESCALAR POR UNA MATRIZ: Sea un escalar cualquier número real positivo o negativo, este número debe multiplicar a cada componente de la matriz. Ejemplo: 5 2 1 4x 3 6 4 = 2 8 3 4x5 4x2 4x1 20 8 4 4x3 4x6 4x4 = 12 24 16 4x2 4x8 4x3 8 32 12 4. MULTIPLICACIÓN DE MATRICES: Dos matrices pueden multiplicarse si solo si el número de columnas de la primera matriz es igual al número de filas de la segunda matriz. Si no se cumple esta condición entonces la multiplicación no se puede realizar. Ejemplo: 1 2 4 2 6 0 4 1 4 3 x 0 1 3 1 2 7 5 2 1x4+2x0+4x2 1x1+2x1+4x7 1x4+2x3+4x5 1x3+2x1+4x2 = 2x4+6x0+0x2 2x1+6x1+0x7 2x4+6x3+0x5 2x3+6x1+0x2 = 12 31 30 13 8 8 26 12 3. CLASIFICACIÓN DE MATRICES: 3.1 MATRIZ CUADRADA: Son las matrices que poseen igual número de filas e igual número de columnas. 3.2 MATRIZ RECTANGULAR: Son las matrices que no poseen el mismo número de filas y el mismo número de columnas. 4. DETERMINANTES (DEFINICIÓN): Es la relación que existe entre una matriz y un número real, sea este positivo o negativo. Solo se determina el determinante de una matriz si ésta es cuadrada es decir; posee el mismo número de filas y el mismo número de columnas. 5. DETERMINANTE DE UNA MATRIZ DE TAMAÑO 2X2: Este método se aplica si solo si la matriz posee dos filas y dos columnas. Ejemplo: 5 2 3 4 det(A)= ( 5x4-2x3) = (20-6)=det(A)=14. 6. DETERMINANTE DE UNA MATRIZ DE TAMAÑO 3X3: Este método se utiliza si solo si la matriz posee tres filas y tres columnas. Ejemplo: 1 2 3 4 2 1 det(A)= (1x2x2)+(2x1x1)+(4x3x3)-(3x2x1)+(2x4x2)+(1x3x1) 1 3 2 = (4+2+36)-(6+16+3) = (42)-(25)= 17. 7. MÉTODO DE COFACTORES A LO LARGO DE LA PRIMERA FILA: Este método se utiliza para matrices de tamaño mayor o igual a tres es decir; para matrices de tamaños 3x3, 4x4, 5x5, etc. Ejemplo: 1 2 3 4 2 1 det(A)= 1 2 1 -2 4 1 +3 4 2 det(A)= 1(2x2-1x3)-2(4x2-1x1)+3(4x3-2x1) 1 3 2 3 2 1 2 1 3 det(A)= 1(4-3)-2(8-1)+3(12-2) det(A)= 1x1-2x7+3x10= 1-14+30=31-14= 17. 8. REGLA DE CRAMER: Este método se aplica solo para matrices de tamaño 3x3, es decir; para matrices que poseen igual número de filas y columnas donde el determinante de la matriz de coeficientes debe ser diferente de cero. Ejemplo: Hallar los valores de las variables x,y,z del sistema de ecuaciones: 2x+4y+6z=18 4x+5y+6z=24 3x+y-2z=4 PROCEDIMIENTO: 1. Evaluar el determinante de la matriz de coeficiente (D): 2 4 6 4 5 6 3 1 -2 Det(D)=(2x5x-2)+(4x6x3)+(4x1x6)-(6x5x3)+(4x4x-2)+(6x1x2) Det(D)=-20+72+24-(90-32+12) Det(D)=-20+72+24-90+32-12 Det(D)=128-122=6 entonces el det(D)=6 es diferente de cero se puede aplicar la regla de Cramer. 2.Hallar el determinante de la matríz D1 donde se sustituye la primera columna de la variable x por la columna de términos independientes: 18 4 6 24 5 6 4 1 -2 Para calcular el determinante de esta nueva matríz se aplica el procedimiento antes ejecutado en la matriz de coeficientes, entonces el det(D1)=24. 3. Calcular el determinante de la matriz D2 se sustituye la segunda columna la columna de las variables y por la columna de términos independientes: 2 18 6 4 24 6 3 4 -2 Se procede a determinar el valor del determinante de la matriz D2 utilizando el procedimiento descrito en los pasos 1 y 2. Entonces el det(D2)=-12. 4. Obtener el determinante de la matriz D3 donde se debe sustituir la columna de la variable z por la columna de términos independientes: 2 4 18 4 5 24 3 1 4 El determinante de la matriz D3 se halla de la misma manera que se determinó en los pasos 2 y 3, entonces el determinante D3=18. 5. Para hallar los valores de las variables x,y ,z se aplican las siguientes fórmulas: X=D1/D Y=D2/D Z=D3/D Y=-12/6=-2 Z=18/6=3. Entonces: X=24/6=4