www.clasesalacarta.com
1
Tema 1.- Números Reales
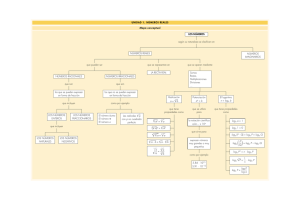
Clasificación de Números Reales
Naturales N
Negativos
Decimales Exactos
Fraccionarios Decimales Periódicos Puros
Decimales Periódicos Mixtos
Enteros
Reales R
Racionales Q
Irracionales
Ι
Z
Racionales (ℚ)
Son todos los números que puede expresarse como el cociente de dos nº enteros, siendo el denominador distinto
de cero
Q=
a
b
a ∈ Z ;b ∈ Z ; b ≠ 0
→
Q=
5
1
2
,- ,- ,…
4
2
2
Enteros (ℤ)
Fraccionarios o Decimales
Son los números sin parte decimal (positivos y
negativos)
Exacto
2,25
ℤ = {...−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}
Periódico Puro
Naturales (ℕ)
2,25252525…
Son los números enteros positivos. Existen los
cardinales (1, 2, 3,…) y los ordinales (1º, 2º,
3º,…)
2,25
Periódico Mixto
2,25813131313…
ℕ= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...}
2,25813
Irracionales (?)?
Son números decimales con un nº ilimitado de cifras decimales no periódicas, es decir, no se pueden expresar
como fracción
2 = 1,414213562…
ϕ=
3= 1,732050808…
1+ 5
= 1.618033989…
2
e = 2,718281828459045…
π = 3.141592654…
Pasar de Decimal a Fracción
Exacto
Periódico Puro
Periódico Mixto
Método I
Método II
Método I
Método II
Método I
Método II
2.38
N = 2.38
2.38
N = 2.38
2.38
N = 2.38
100 N = 238
238 119
=
100
50
238
N=
100
119
=
50
10 N = 23.8
100 N = 238.38
238-2
236
=
99
99
100N =
- N =
238.38
2.38
99N =
N=
236
236
99
238-23
215
=
90
90
=
43
18
10 ·10N = 238.8
100N =
- 10N =
90N =
N=
238.8
23.8
215
215
43
=
90
18
Bárbara Cánovas Conesa
2
Matemáticas _ B_ 4º ESO
Concepto de Números Reales
Es el conjunto de los números Racionales e
Irracionales (son todos los nº!!!!!!)
R
Q Z
I
Nos permiten hacer todas las operaciones, menos
PAR
nº < 0 y la división por cero
N
Representación de Números Reales sobre la Recta Real
Enteros o Decimales
Exactos
Decimales Periódicos
1.83 =
11
11
=
6
1
6
=1+
5
5
6
Irracionales
Cuadráticos
2
2
5 = 2 +1
1º
3º
3.4
0
1
2
3
Irracionales: Aproximación
2 = 1.414213562…
0
1
2
3
1.3
1.4
1.5
1.6
12 5
4
2º
1
4º
0
22
2
2
1.40 1.41 1.42 1.43
…
Operaciones de Números Reales
Suma: Propiedades
1. Interna: el resultado de sumar dos nº reales es otro número real: a + b ℝ
2. Asociativa: el modo de agrupar los sumandos no varía el resultado: (a + b) + c = a + (b + c)
3. Conmutativa: el orden de los sumandos no varía el resultado : a + b = b + a
4. El elemento neutro de la suma es el 0 porque todo nº sumado con él da el mismo nº: a + 0 = a
5. Elemento opuesto: dos números son opuestos si al sumarlos obtenemos como resultado el cero. El opuesto
del opuesto de un número es igual al mismo número.
Producto: Propiedades
1. Interna: el resultado de multiplicar dos números reales es otro número real: a · b ℝ
2. Asociativa: el modo de agrupar los factores no varía el resultado: (a · b) · c = a · (b · c)
3. Conmutativa: el orden de los factores no varía el producto: a · b = b · a
4. El elemento neutro de la multiplicación es el 1 porque todo nº multiplicado por él da el mismo nº: a ·1 = a
5. Elemento inverso: un nº es inverso del otro si al multiplicarlos obtenemos como resultado el elemento
unidad (1) : a ·
1
a
=1
6. Distributiva: el producto de un nº por una suma es igual a la suma de los productos de dicho nº por cada
uno de los sumandos: a · (b + c) = a · b + a · c
7. Sacar factor común: es el proceso inverso a la propiedad distributiva. Si varios sumandos tienen un factor
común, podemos transformar la suma en producto extrayendo dicho factor: a · b + a · c = a · (b + c)
www.clasesalacarta.com
3
Tema 1.- Números Reales
Diferencia
División
a − b = a + (−b)
Es el producto del dividendo por el inverso del divisor
10 ÷ 5 = 10 ·
1
10
=
=2
5
5
Intervalo
Conjunto de nº reales comprendidos entre otros dos nº: a y b (extremos del intervalo)
Nombre
Símbolo
Significado
Representación
Intervalo Abierto
(a, b)
x/a < x < b
a
b
Intervalo Cerrado
[a, b]
x/a ≤ x ≤ b
a
b
Intervalo Semiabierto
por la Izquierda
(a, b]
x/a < x ≤ b
a
b
Intervalo Semiabierto
por la Derecha
[a, b]
x/a ≤ x < b
a
b
Semirrecta
Está determinada por un nº. En una semirrecta se encuentran todos los nº mayores (o menores) que él
Recta Real ℝ = -∞,+∞
Nombre
Símbolo
Significado
x<a
-∞, a
{x R / - < x < a}
xa
-∞, a
{x R / - < x a}
x>a
a, +∞
{x R / a < x < +}
x a
a, +∞
{x R / a x < +}
Representación
a
a
a
a
Valor Absoluto de un Nº Real
a =
-a
+a
si a<0
si a>0
3 =3
-3 = 3
x =3
x >3
x < -3
ó
x>3
x = -3
x=3
(-, -3) (3, +)
x < 3 -3 < x < 3
x - 3 < 7 -7 < x - 3 < 7
x (-3, 3)
-7 + 3 < x < 7 + 3
-4 < x < 10
Bárbara Cánovas Conesa
Matemáticas _ B_ 4º ESO
Propiedades
a·b = a · b
a = -a
a + b
a + b
Distancia
d (a, b) = |b − a|
Entornos: Er(a) E(a,r)
Un entorno de centro a y radio r, es el intervalo abierto (a - r, a + r)
-r
a
+r
Er(a) = (a - r, a + r) |x - a|< r a - r < x < a + r
Entornos laterales
Por la izquierda
Por la derecha
Er(a-) = (a - r, a]
Er(a+) = [a, a + r)
a
a-r
a+r
a
Entorno reducido
Se usa para saber qué pasa en las proximidades del punto, sin que interese lo que ocurre en dicho punto
E r*(a) = {x (a - r, a + r), x ≠ a}
-r
a
+r
Potencias
n
a0 = 1
a×b
n
= an × b
a1 = a
a÷b
n
= an ÷ b
am × an = am + n
n
a-m =
am ÷ an = am - n
m n
a
m×n
=a
a
b
-m
=
b
a
1
am
m
m
=
b
am
4
www.clasesalacarta.com
5
Tema 1.- Números Reales
Notación Científica
2,75·10
12
-12
= 2.750.000.000.000
2,75·10
= 0,000000000275
Suma y Resta
9
12
5,83·10 + 6,932·10
- 7,5·10
10
9
9
9
9
12
= 5,83·10 + 6932·10 - 75·10 = 6862,83·10 = 6,86283·10
Multiplicación, División y Potencia
9
5,8·10 × 6,9·10
12
9
5,8·10 ÷ 6,9·10
5,8·10
9 2
= 5,8 × 6,9 ·10
12
9+12
= 5,8 ÷ 6,9 ·10
2
= 5,8
9 2
· 10
21
= 40,02·10 = 4,002·10
9-12
-3
= 0,84·10
= 33,64·10
18
22
-4
= 8,4·10
= 3,364·10
19
Raíces
ÍNDICE
n
Radicando →
+n a
-n a
a < 0 → ∃ raíz de índice impar
a≥0→∃
a →
Forma Exponencial
a
m
n
=
n
am
Propiedades
n×p
ap = n a
n
n
n
a×
n
a
m n
a
=
b
b
n
a = m × n a : Raíz
n
n
b= a×b
a
p
=
n
ap
Suma o Diferencia
8 + 18 +
4
3
2
2500 = 2 + 2 × 3 +
4
5
4
2 × 5 = 2 2 + 3 2 + 5 2 = 10 2
Multiplicación y División
Mismo Índice
3· 4 =
3·4 =
12
Reducción a índice común
3
2
2 ÷
4
3
3 → m.c.m
3, 4
=12 →
12
2
2
12
3
12
÷
3
3
12
4
=
12
2
2 4
÷
12
3 3
3
=
12
2
8
÷
12
9
3 =
12
8
2
39
Bárbara Cánovas Conesa
6
Matemáticas _ B_ 4º ESO
Racionalización de Denominadores
a
b
a
m
b
a
b+ c
→
b
a
→
c
a
→
m
c
b
a
b+ c
b
·
b
a
·
m
m-c
b
b- c
·
b- c
1
→
25
→
→
1
3
25
1
5- 3
1
=
25
=
=
1
3
5
25
×
2
1
5- 3
25
=
·
3
1
3
5
25
5
=
2
·
5+ 3
5+ 3
3
=
3
𝟓3 - 2
=
𝟓3 - 2
5
5
5+ 3
5+ 3
=
25 - 3
22
Números Aproximados
Cifras Significativas
Son los dígitos de un número que consideramos no nulos. Son las que se saben con exactitud
Norma
Ejemplo
Todos los dígitos 0
1.457 4 cifras significativas 1
Los 0 situados entre 2 cifras significativas (nº 0)
1.407
4 cifras significativas
Los 0 a la izquierda de la primera cifra significativa (nº 0)
0.057 2 cifras significativas
Para nº > 1, los 0 a la derecha de la coma
3.00 3 cifras significativas
¡OJO!
Para nº sin coma decimal, los ceros posteriores a la última cifra
3 · 102 1 cifra significativa
0, pueden o no considerarse significativos????
3’0 · 102 2 cifras significativas
Se evita con la notación científica
Redondeo
Redondeo con 3 cifras significativas o a las unidades:
123,421 ≅ 123,000
123,521 ≅ 124,000
123,721 ≅ 124,000
Control del Error Cometido
Error Absoluto = Valor Rea l- Valor Aproximado
Error Relativo =
Error Absoluto
Valor Real
Las cotas de los errores son cantidades mayores o iguales que los errores con menor o igual número de cifras
significativas
www.clasesalacarta.com
Tema 1.- Números Reales
Logaritmos
argumento
log a x = y
logaritmo
base
loga x = y → ay = x
→
a>0
a≠0
2
log2 4 = 2 → 2 = 4
Propiedades
∄ log
-a
x
loga xn = n loga x
loga a = 1
loga an = n
∄ loga -x
∄ loga 0
loga
loga x · y = loga x + loga y
loga 1 = 0
loga
n
x =
1
loga x
n
Cambio de base
x
= loga x - loga y
y
loga x =
logb x
logb a
Logaritmos decimales
Base 10
log10 x = log x
Logaritmos neperianos
Base nº e
Lne x = Ln x
Ln x · y = Ln x + Ln y
Ln 1 = 0
Ln x
= Ln x - Ln y
Ln y
Ln e = 1
n
Ln e = n
Ln xn = n · Ln x
Ln
n
x=
1
Ln x
n
7