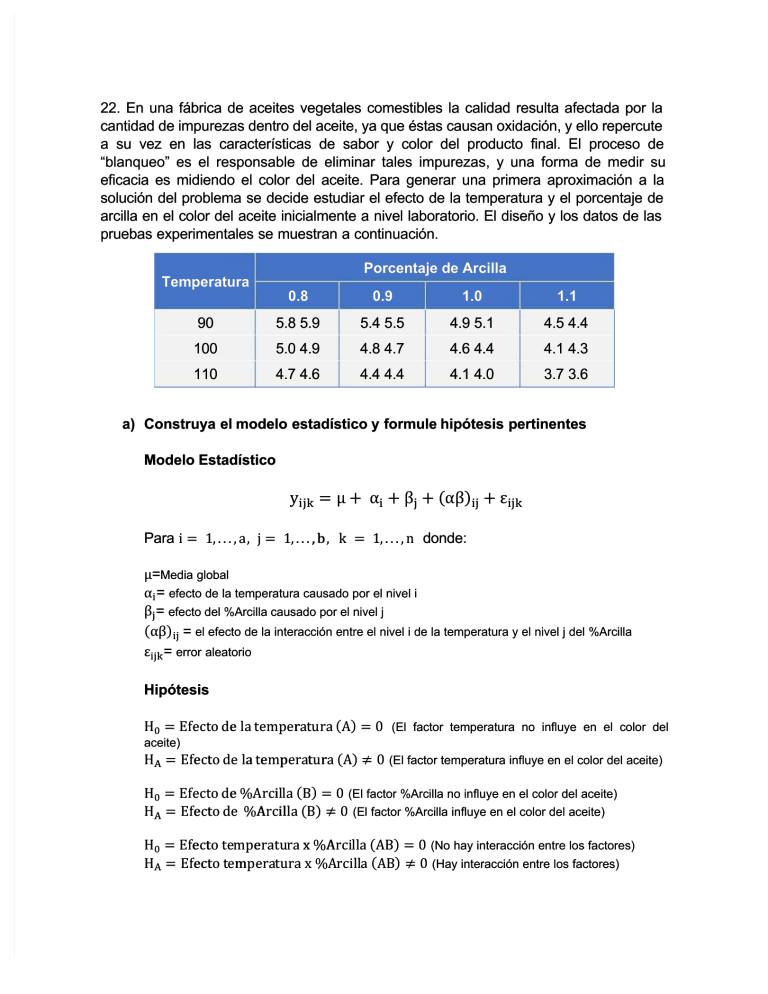
22. En una fábrica de aceites vegetales comestibles la calidad resulta afectada por la cantidad de impurezas dentro del aceite, ya que éstas causan oxidación, y ello repercute a su vez en las características de sabor y color del producto final. El proceso de “blanqueo” es el responsable de eliminar tales impurezas, y una forma de medir su eficacia es midiendo el color del aceite. Para generar una primera aproximación a la solución del problema se decide estudiar el efecto de la temperatura y el porcentaje de arcilla en el color del aceite inicialmente a nivel laboratorio. El diseño y los datos de las pruebas experimentales se muestran a continuación. Porcentaje de Arcilla Temperatura 0.8 0.9 1.0 1.1 90 5.8 5.9 5.4 5.5 4.9 5.1 4.5 4.4 100 5.0 4.9 4.8 4.7 4.6 4.4 4.1 4.3 110 4.7 4.6 4.4 4.4 4.1 4.0 3.7 3.6 a) Construya el modelo estadístico y formule hipótesis pertinentes Modelo Estadístico y μ + α + β + (αβ) αβ) + ε Para i 1,...,a 1,...,a,, j 1,...,b 1,...,b,, k 1,...,n 1,...,n donde: μ=Media global α= efecto de la temperatura causado por el nivel i β= efecto del %Arcilla causado por el nivel j (αβ) αβ) = el efecto de la interacción entre el nivel i de la temperatura y el nivel j del %Arcilla ε= error aleatorio Hipótesis H Efecto de la temperatura temperatura (A) 0 (El factor temperatura no influye en el color del aceite) H Efecto de la temperatura temperatura((A) ≠ 0 (El factor temperatura influye en el color del aceite) H Efecto de %Arcilla %Arcilla (B) 0 (El factor %Arcilla no influye en el color del aceite) H Efecto de %Arcilla (B) ≠ 0 (El factor %Arcilla influye en el color del aceite) H Efecto temperatu temperaturara x %Arcilla %Arcilla (AB) AB) 0 (No hay interacción entre los factores) H Efecto tempera temperatura tura x %Arcill %Arcillaa (AB) ≠ 0 (Hay interacción entre los factores) b) ¿Cuál es el nombre del diseño utilizado? Diseño factorial completo 4x3 con 2 réplicas c) Por lo general, a condiciones reales se utiliza 1.1% de arcilla y 100 grados de temperatura. ¿Por qué cree que se eligieron precisamente esos niveles de prueba para el experimento? Porque tal vez estos niveles de prueba son los que mejor funcionan para este caso en particular y proporcionan mayor calidad de datos. d) Realice un análisis de varianza para probar las hipótesis y obtenga conclusiones. Sumatoria de las observaciones B A 1 2 3 4 1 2 3 11,7 9,9 9,3 30,9 10,9 9,5 8,8 29,2 10 9 8,1 27,1 8,9 8,4 7,3 24,6 41,5 36,8 33,5 …111,800 Entonces, a=3 b=4 n= 2 N= a*b*n= 24 = total en el nivel i del factor A = total en el nivel j del factor B …= suma de todas las observaciones +36,8 +33,5 111,800 41,5 … ∑ − ∑ − 24 4 ∗ 2 = = 4.198,74 − 12.499,24 8 24 524,843 − 520.802 , +29,2 +27,1 +24,6 111,800 30,9 … ∑ − ∑ − 24 3 ∗ 2 = = 524,503 − 520.802 , 3.147,02 − 12.499,24 6 24 2 ∑∑ − … − − = = +9,9 +9,3 +10,9 +9,5 +8,8 + 10 + 9 +8,1 +8,9 +8,4 +7,3 11,7 ∑∑ 2 = = 111,800 − 24 − 4,040−3,701 1.057,56 111,800 ∑∑ 2 − 24 − 4,0 40 − 3,7 01 528,7 8− 520.8 02 − 4,0 40 − 3,7 01 = = , 2 ∑ ∑ ∑ − … 528,88− 111,800 24 = = = 2 528,88− 520.802 , − − − 8,078 − 4,040 − 3,701 − 0,237 , Tabla de análisis de varianza (ANOVA) Fuente de variabilidad (efecto) (F.V) Suma de cuadrados (S.C) Temperatur a (A) 4,04083 % Arcilla (B) Interacción (AB) 3,70166 0,23583 Error 0,1 Total 8,07833 Grados de libertad (G.L) a-1 = 3-1 =2 b-1 = 4-1 =3 (a-1)(b-1) =2*3 =6 ab(n-1) =3*4(2-1) =12 abn1=(3*4*2)-1 =23 Cuadrado medio (CM) . =2,0204 , =1,2338 , =0,039305 , =0,0083 Estadístico de prueba () 2,0204 0.008333 significancia observada (Valor –p) 0,000 0,000 =4,716 .,, .,, =3,49 =148,066 0,039305 0,008333 =3,89 =245,45 1,2338 0.008333 Valor crítico para 0,011 .,, =3,00 El análisis de varianza permite concluir que, tanto para el factor A como el factor B, temperatura y porcentaje de arcilla respectivamente, se rechaza H 0 debido a que en ambos caso es muy grande, mucho mayor al , de igual forma, el es menor que la significancia prefijada por lo cual se contradice la hipótesis de que no hay 0,05 efectos.. − < Para el caso de la interacción, se evidencia una interacción entre los factores. Por tanto rechaza H0 , el es mayor al , y el es menor que la significancia prefijada . 0,05 − < e) Apoyándose en las gráficas de efectos, ¿cuál es la relación general entre el color y los factores controlados en su rango de experimentación? De acuerdo con las gráficas de efectos, en el cual se ve que a mayor temperatura y mayor porcentaje de arcilla se minimiza el color del aceite, y a menor temperatura y menor porcentaje de arcilla el color es mas alto. f) A partir de la gráfica de interacciones, ¿cree que haya un efecto no lineal? En la grafica de interacciones se ven lineas con pendientes relati vamente diferentes, pero claramete se evidencia un efecto lineal. g) Considerando que el nivel mínimo aceptable de blancura es de 4.8, ¿qué tratamiento utilizaría? El tratamiento más óptimo para cumplir con ese requerimiento sería Factor A en nivel 3 y Factor B en nivel 1. h) ¿Vale la pena plantear el estudio en condiciones reales? Dado que el diseño factorial ha permitido investigar todas las posibles combinaciones de los niveles de los factores, permitiendo conocer qué factores son más importantes y cuál es el tratamiento que más conviene, plantear el estudio en condiciones reales permitiría ver resultados más explícitamente, por tanto, si valdría la pena plantearlo. i) ¿Qué cambio le haría al experimento si lo corre en condiciones reales? Disminuiría un nivel del porcentaje de Arcilla y aumentaría la cantidad de réplicas que permitiera la obtención de un resultado más robusto y confiable.









