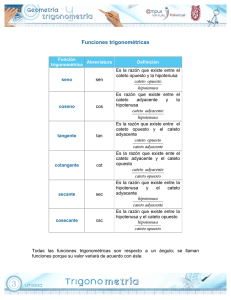
3 MATEMÁTICAS SECUNDARIA o 1. Razones trigonométricas 2. Qué vamos a aprender: Resuelve problemas utilizando las razones trigonométricas seno, coseno, tangente. Materiales: Fichas didácticas, cuaderno de apuntes, lápiz, lapicero, calculadora. 50 min. Semana del 15 al 19 de febrero de 2021 Te explico: En esta secuencia iniciaremos con una breve explicación de los términos con los que se va a trabajar. Razones trigonométricas 2 Las razones trigonométricas son relaciones entre los lados del triángulo y sólo dependen de los ángulos de éste. Las razones trigonométricas básicas son tres: seno, coseno y tangente. Por ejemplo, el coseno de un ángulo es la relación entre el cateto contiguo (el que toca al ángulo) y la hipotenusa. Ejemplos: El cateto opuesto es el lado que está enfrente del ángulo dado. El cateto adyacente es el lado que está junto al ángulo dado, y que no es la hipotenusa. Para aprender más: Funciones trigonométricas: https://www.youtube.com/watch?v=8zVW0U2jn8U 3 MATEMÁTICAS o Manos a la obra SECUNDARIA ¿Qué cambia y qué no cambia? 1. En la secuencia 7 se utilizó la imagen de una escalera recargada en una pared, la cual podía representarse mediante un triángulo rectángulo. Esta situación está representada en las siguientes imágenes. Con base en ellas, respondan las preguntas y completen la tabla, donde c significa cociente. ¿Por qué son semejantes los triángulos?________________________________ A Longitud de la escalera Distancia de la escalera a la pared Altura que alcanza la escalera a la pared Ángulo que forma la escalera con el piso C1= altura que alcanza en la pared Longitud de la escalera C2= distancia de la escalera la pared Longitud de la escalera C3= altura que alcanza la pared_______ Distancia de la escalera a la pared B Situación C D 3 MATEMÁTICAS o SECUNDARIA Cateto opuesto, cateto adyacente 1. Analicen los siguientes triángulos rectángulos y contesten las preguntas a) ¿Son semejantes entre sí? b) Argumenten su respuesta. 2. En cada triángulo se ha marcado con rojo el cateto adyacente al ángulo de 36.87° y con azul el cateto opuesto a dicho ángulo. Analícenlos y escriban con sus palabras lo que se pide. En un triángulo rectángulo, el cateto. • Adyacente a un ángulo es _____________________________ • Opuesto a un ángulo es _______________________________ 3. En los siguientes triángulos, anoten 90º al ángulo recto, h a la hipotenusa, identifiquen el ángulo M con un arco y escriban co al cateto opuesto y ca al cateto adyacente del ángulo. N P M 3 MATEMÁTICAS SECUNDARIA o 4. Tomen en cuenta los triángulos de la actividad 1 de la página 72. Usen las medidas que sean necesarias y completen la tabla. Consideren que el cateto opuesto y el cateto adyacente se refieren al ángulo M, que mide 36.87°. Triangulo co ca h co_ h ca_ h co_ ca A B C D E Razones interesantes e importantes. 1. Lee la siguiente información. En las actividades anteriores calculaste estos cocientes. C1= cateto opuesto hipotenusa c2= cateto adyacente hipotenusa c3= cateto opuesto cateto adyacente Estos cocientes reciben el nombre de razones trigonométricas y cada uno tiene un nombre especial. Si consideramos el ángulo P, en el triángulo de abajo tenemos que: P h ca Q Razón cateto opuesto hipotenusa cateto adyacente hipotenusa cateto opuesto cateto adyacente co R Nombre seno del ángulo P coseno del ángulo P tangente del ángulo P Se simboliza sen P= co h cos P= ca h tan P= co ca 3 MATEMÁTICAS o 2. Con base en la información anterior, midan lo que consideren necesario y calculen lo que se pide. SECUNDARIA A G E B C R F S T sen S =_____________________________________ cos S =____________________________________ tan S = ____________________________________ sen C = _____________________________________ cos C = _____________________________________ tan C = _____________________________________ sen G = _____________________________________ cos G =______________________________________ tan G=______________________________________ 3. En un triángulo rectángulo, identificado como MNP, se sabe que el ángulo recto está en N, que el cateto NP mide 6 cm y que el sen M = 3/5 a) Diseñen en su cuaderno un esquema del problema. b) ¿Cuánto mide la hipotenusa de este triángulo? ¿De qué depende? 1. Consideren los siguientes triángulos rectángulos, tomen las medidas indicadas y completen la tabla. 3 MATEMÁTICAS o SECUNDARIA P Triangulo Medidas del co al ángulo P Medidas del ca al ángulo P Medidas de la hipotenusa Sen P Cos P Tan P Q R PQR QR= PST PUV ST= VU= PQ= PS= PU= a) ¿Son semejantes los triángulos? _________________________ b) Argumenten su respuesta. _______________________________ S U T V 3 MATEMÁTICAS o SECUNDARIA Repaso y practico Los valores de las razones 1. Para construir una tabla de valores de las razones seno, coseno y tangente de algunos ángulos. Para ello, calculen el valor del lado y del ángulo que falta a cada triángulo y completen la tabla de la siguiente página. Ángulo Seno Coseno Tangente 10º 20º 30º 45º 50º 2. Del siguiente triángulo rectángulo sólo se conoce la medida del cateto adyacente al ángulo de 70°. Planeen la manera de calcular la medida del otro cateto y de la hipotenusa. Cuando lo hayan hecho, anoten su procedimiento y el resultado. Lo que aprendí Rellene los círculos si observa que su hijo (a) logró lo siguiente: Leyó la información de los temas y comprendió los conceptos de razones trigonométricas, las funciones trigonométricas (seno, coseno, tangente), los valores de las razones. Pudo resolver los ejercicios de la sección manos a la obra. Resolvió los ejercicios finales y los integro a su carpeta de experiencias.