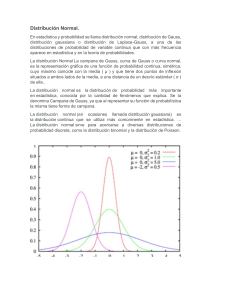
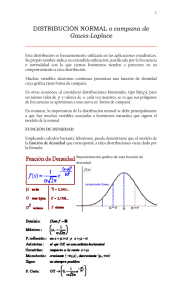
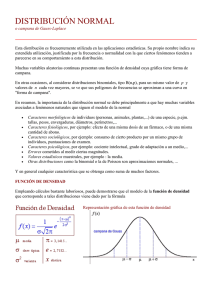
HISTORIA Distribución Normal o de Gauss: La distribución normal fue reconocida por primera vez por el francés Abraham de Moivre (1667-1754). Posteriormente, Carl Friedrich Gauss (1777-1855) elaboró desarrollos más profundos y formuló la ecuación de la curva; de ahí que también se le conozca, más comúnmente, como la “campana de Gauss”. QUE ES LA DISTRIBUCION NORMAL La distribución normal se conoce como la curva de Gauss o campana de Gauss, famoso matemático alemán del siglo 19. Distribución Normal: Esta distribución es frecuentemente utilizada en las aplicaciones estadísticas. Su propio nombre indica su extendida utilización, justificada por la frecuencia o normalidad con la que ciertos fenómenos tienden a parecerse en su comportamiento a esta distribución. Muchas variables aleatorias continuas presentan una función de densidad cuya gráfica tiene forma de campana. En otras ocasiones, al considerar distribuciones binomiales, tipo B(n,p), para un mismo valor de p y valores de n cada vez mayores, se ve que sus polígonos de frecuencias se aproximan a una curva en «forma de campana. CARACTERES Caracteres morfológicos de individuos (personas, animales, plantas,…) de una especie, por. Ejemplo: Tallas, pesos, envergaduras, diámetros, perímetros… Caracteres fisiológicos, por ejemplo; efecto de una misma dosis de un fármaco, o de una misma cantidad de abono. Caracteres sociológicos, por ejemplo: consumo de cierto producto por un mismo grupo de individuos, puntuaciones de examen. Caracteres psicológicos, por ejemplo: cociente intelectual, grado de adaptación a un medio…… Errores cometidos al medir ciertas magnitudes. Valores estadísticos maestrales, por ejemplo: la media. Otras distribuciones como la binomial o la de Poisson son aproximaciones normales. Características Algunas de las características más representativas de la distribución normal son las siguientes: 1. Media y desviación típica A la distribución normal le corresponde un media cero y una desviación típica o estándar de 1. La desviación típica o estándar indica la separación que existe entre un valor cualquiera de la muestra y la media. 2. Porcentajes En una distribución normal, se puede determinar con exactitud qué porcentaje de los valores estará dentro de cualquier rango específico. Por ejemplo: Alrededor del 95% de las observaciones está dentro de 2 desviaciones estándar de la media. El 95% de los valores se ubicará dentro de 1.96 desviaciones estándar con respecto a la media (entre −1.96 y +1.96). Aproximadamente el 68% de las observaciones está dentro de una 1 desviación estándar de la media (-1 a +1), y alrededor del 99.7% de las observaciones estarían dentro de 3 desviaciones estándar con respecto a la media (-3 a +3). Función de densidad Se dice que una variable aleatoria continua X sigue una distribución normal de parámetros μ y σ y se denota X~N (μ, σ) si su función de densidad está dada por: donde μ (miu) es la media y σ (sigma) es la desviación típica (σ2 es la varianza). Se llama distribución normal "estándar" a aquélla en la que sus parámetros toman los valores μ = 0 y σ = 1 En este caso la función de densidad tiene la siguiente expresión: El Teorema del Límite Central • El Teorema del límite central asegura que la distribución de muestreo de la media se aproxima a la normal al incrementarse el tamaño de la muestra. • La importancia práctica del Teorema del límite central es que nos permite usar estadística de muestra para hacer inferencias con respecto a los parámetros de población, sin saber sobre la forma de la distribución de frecuencia de esa población más que lo podamos obtener de la muestra. • Una distribución binomial de parámetros n y p es aproximadamente normal para grandes valores de n, y p no demasiado cercano a 1 ó 0 (algunos libros recomiendan usar esta aproximación sólo si n y n (1 − p) son ambos, al menos, 5; en este caso se debería aplicar una corrección de continuidad).La normal aproximada tiene parámetros μ = np, σ2 = np(1 − p). PROBLEMA El catedrático requiere mantener en su clase de matemáticas un promedio de 69.2, está variable normalmente distribuida tiene una desviación estándar de 13.4. Cuál es la probabilidad de que las notas entre 50 y 58 contribuyan a mantener el promedio? Solución: X=50 x = 58 Z=50-69.2/13.4 z = 58 – 69.2/13.4 Z = -1.43 z = 0.84 -1.43 -0.84 0 P (-1.43 < z < -0.84) A (-1.43, – 0.84) = a (-1.43, 0) – A (-0.84, 0) = 0.4236 – 0.2996 =0.124 P (50 < x < 58) = 0.124 B) Cual es la probabilidad de que las notas mayores que 80 contribuyan a mantener el promedio? X > 80 x = 80 Entonces z = 80 – 69.2/13.4 =0.81 P(x > 80) = P (z > 0.81) A = (0.81, + = = 0.791 P (z > 0.81) = 0.791 …………… 79.1% CONCLUSIONES • La distribución normal es la más usada en la probabilidad y la estadística, dado a que muchas poblaciones numéricas tienen distribuciones que se ajustan con precisión a una curva normal. • El teorema central del límite nos permite aproximar la distribución binomial en una distribución normal https://rksbet.wordpress.com/2013/02/26/historia-de-la-distribucionnormal/#:~:text=Distribuci%C3%B3n%20Normal%20o%20de%20Gauss%3A%20L a%20distribuci%C3%B3n%20normal,conozca%2C%20m%C3%A1s%20com%C3 %BAnmente%2C%20como%20la%20%E2%80%9Ccampana%20de%20Gauss% E2%80%9D. https://www.slideserve.com/bonita/distribucion-normal https://psicologiaymente.com/cultura/distribucion-normal