Distribución Normal: Monografía de Enfermería y Tecnología Médica
Anuncio

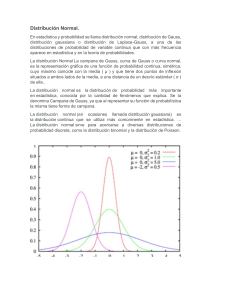
“Año de la lucha contra la corrupción e impunidad” FACULTAD DE CIENCIAS DE LA SALUD ESCUELA PROFESIONAL DE CIENCIAS DE LA SALUD CARRERA PROFESIONAL DE ENFERMERÍA Y TÉCNOLOGIA MÉDICA TÍTULO DISTRIBUCIÓN NORMAL AUTORES: APAGÜEÑO SALAZAR, Elma GORDON FLORES, Jesús Solange LOZANO ACHANG, Nataly LOAYZA RAMÍREZ, Katia Consuelo RENGIFO VARGAS, Adriana Vanesa TORRES GUTIÉRREZ, Jhoselyn Alexandra VELA ALTAMIRANO, Bill Austin ASESOR: Lic. Yoshi, ENCINAS CHONG IQUITOS – PERÚ 2019 1 DEDICATORIA Al padre celestial, por la vida y brindarnos sabiduría e entendimiento para realizarnos como profesionales, por haber puesto en nuestro camino a personas que han sido nuestro soporte. A nuestros padres, por su amor incondicional, su apoyo, sus consejos y los valores que siempre nos inculcan, es lo que hizo de nosotras personas de bien y con ansias de superación profesional. A mi profesor por ser paciente para explicarme el trabajo, por ser un ejemplo a seguir, por confiar en mí y por todo el apoyo que me ha brindado en mi trabajo monográfico. 2 AGRADECIMIENTO Agradecemos a Dios por la salud y las fuerzas que nos concede y a nuestros padres por su apoyo incondicional. Mis Familiares, Amigos, Profesores y Autoridades Institucionales. A la Facultad de Ciencias de la Salud de la Universidad científica del Perú, por acogerme dentro de sus aulas haciendo posible el logro de mí meta. A mi profesor por facilitarnos la información necesaria para el desarrollo de la Investigación de nuestro trabajo. 3 Contenido DEDICATORIA ................................................................................................................................ 2 AGRADECIMIENTO ........................................................................................................................ 3 RESUMEN ...................................................................................................................................... 5 INTRODUCCIÓN ............................................................................................................................. 6 CAPITULO I: DISTRIBUCIÓN NORMAL ........................................................................................... 7 1.2. DEFINICIÓN......................................................................................................................... 7 2.2. LA IMPORTANCIA DE LA DISTRIBUCIÓN NORMAL ............................................................. 7 2.2.1. ¿Por qué la distribución normal es tan importante? .................................................. 7 2.2.2. ¿Qué significa Normalidad? ........................................................................................ 8 2.2.3. PROPIEDADES DE LA DISTRIBUCIÓN NORMAL ............................................................ 9 2.2.4. CARACTERISTICAS DE LA DISTRIBUCIÓN NORMAL ..................................................... 9 2.2.5. FORMULAS DE LA DISTRIBUCION NORMAL .............................................................. 10 2.2.6. DISTRIBUCIÓN NORMAL O GAUSSIANA .................................................................... 11 2.2.7. CURVA NORMAL ........................................................................................................ 12 2.2.8. TIPIFICACIÓN MANEJO DE TABLAS ............................................................................ 13 2.2.9. EJERCICIOS ................................................................................................................. 14 CONCLUSIÓN ............................................................................................................................... 16 BIBLIOGRAFIA .............................................................................................................................. 17 ANEXO ......................................................................................................................................... 18 4 RESUMEN El concepto de distribución normal fue presentado por primera vez por Abraham de Moivre estadístico francés en el siglo XVIII en un artículo del año 1733, que fue reimpreso en la segunda edición, del año 1738, en el contexto de cierta aproximación de la distribución binominal para grandes valores de n. Su resultado fue ampliado por “Laplace”, en su libro “Teoría analítica de las probabilidades”, en el año de 1812, y en la actualidad se llama Teorema de Moivre Laplace. Laplace usó la distribución normal en el análisis de errores de experimentos. El importante método de mínimos cuadrados fue introducido por “Legender en el año 1805”. Gauss, que afirmaba haber usado el método desde el año 1794, lo justificó rigurosamente en 1809 asumiendo una distribución normal de los errores. El nombre de Gauss se ha asociado a esta distribución porque la usó con profusión cuando analizaba datos astronómicos y algunos autores le atribuyen un descubrimiento independiente del de Moivre. Esta distribución es frecuentemente utilizada en las aplicaciones estadísticas. Su propio nombre indica su extendida, utilización, justificada por la frecuencia o normalidad con la que ciertos fenómenos tienden a parecerse en su comportamiento a esta distribución. Muchas variables aleatorias continuas presentan una función de densidad cuya grafica tiene forma de campana. En resumen, la importancia de la distribución normal se debe principalmente que hay muchas variables asociadas a fenómenos naturales que siguen el modelo de la normal. 5 INTRODUCCIÓN Este trabajo se centra en la distribución normal, una de las distribuciones más importantes en estadística. Es una distribución de variable continua, con campo de variación. Fue descubierta por Gauss al estudiar la distribución de los errores en las observaciones astronómicas. Debe su importancia a tres razones fundamentales. Por un lado, un gran número de fenómenos reales se pueden modelizar con esta distribución tales el caso de las características cuantitativas de casi todas las grandes poblaciones, por otro lado, muchas de las distribuciones de uso frecuente tienden a aproximarse a la distribución normal bajo ciertas condiciones, y por último, en virtud del “Teorema Central del Límite”, todas aquellas variables que puedan considerarse causadas por un gran número de pequeños efectos como pueden ser los errores de observación tienden a distribuirse con una distribución normal. Caracteres morfológicos de individuos de una especie ya sean (persona, animal, plantas). Por ejemplo: talla, peos, envergaduras, diámetros, perímetros. Caracteres fisiológicos, por ejemplo: efecto de una misma dosis de un fármaco, o de una misma cantidad de avino. Caracteres sociológicos, por ejemplo: consiente intelectual, grada de adaptación a un medio. Errores cometidos al medir ciertas magnitudes. Valores estadísticos maestrales, por ejemplo: la media. Otras distribuciones como la binomial o la poisson son aproximaciones normales. En general cualquier característica que se obtengan como suma de muchos factores. 6 CAPITULO I: DISTRIBUCIÓN NORMAL 1.2. DEFINICIÓN Abraham de Moivre estadístico francés, enunció la ley de probabilidades compuesta e inició el empleo de las ecuaciones de diferencias finitas, que posteriormente debía generalizarse. Introductor de la trigonometría con cantidades imaginarias, demostró la fórmula (cos x + i sen xm = cos mx + i sen mx 1730) llamada fórmula de Moivre. La distribución normal es la distribución de probabilidad más importante en estadística, conocida por la cantidad de fenómenos que explica. Se la denomina Campana de Gauss, ya que al representar su función de probabilística la misma tiene forma de campana. 2.2. LA IMPORTANCIA DE LA DISTRIBUCIÓN NORMAL 2.2.1. ¿Por qué la distribución normal es tan importante? El Teorema del Límite Central, la palabra normal viene de la palabra griega normalis, que significa conforme a la regla, a la norma. Que es lo típico que se repite muchas veces según la experiencia. Aplicado a los histogramas, que es típico encontrarse con histogramas normales. La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro estadístico. Esta curva se conoce como campana de Gauss y es el gráfico de una función gaussiana. La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos. Mientras que los mecanismos que subyacen a gran parte de este tipo de fenómenos son desconocidos, por la enorme cantidad de variables incontrolables que en ellos intervienen, el uso del modelo normal puede justificarse asumiendo que cada observación se obtiene como la suma de unas pocas causas independientes. De hecho, la estadística descriptiva sólo permite describir un fenómeno, sin explicación alguna. 7 La distribución normal también es importante por su relación con la estimación por mínimo cuadrado, uno de los métodos de estimación más simples y antiguos. Algunos ejemplos de variables asociadas a fenómenos naturales que siguen el modelo de la normal son: Caracteres morfológicos de individuos como la estatura Caracteres fisiológicos como el efecto de un fármaco Caracteres sociológicos como el consumo de cierto producto por un mismo grupo de individuos. Caracteres psicológicos como el cociente intelectual. Nivel de ruido en telecomunicaciones. Errores cometidos al medir ciertas magnitudes. La distribución normal también aparece en muchas áreas de la propia estadística. Por ejemplo, la distribución muestral de las medias muestrales es aproximadamente normal, cuando la distribución de la población de la cual se extrae la muestra no es normal. Además, la distribución normal maximiza la entropía entre todas las distribuciones con media y varianza conocidas, lo cual la convierte en la elección natural de la distribución subyacente a una lista de datos resumidos en términos de media muestral y varianza. La distribución normal es la más extendida en estadística y muchos test estadísticos están basados en una normalidad más o menos justificada de la variable aleatoria bajo estudio. En probabilidad, la distribución normal aparece como el límite de varias distribuciones de probabilidad continuas y discretas. 2.2.2. ¿Qué significa Normalidad? Ya sabes que los datos pueden representarse mediante histogramas. Durante muchos años se ha visto que muchos de los datos recogidos de la realidad tienen un histograma en forma de montaña, simétricos. 8 Ecuaciones: La campana de Gauss está definida por la función: 2.2.3. PROPIEDADES DE LA DISTRIBUCIÓN NORMAL La distribución normal posee ciertas propiedades importantes que conviene destacar: Tiene una única moda, que coincide con su media y su mediana. La distancia entre la línea trazada en la media y el punto de inflexión de la curva es igual a una desviación típica. Tiene forma de campana (es simétrica). Sus medidas de tendencia central son idénticas (media, mediana, moda, rango medio y eje medio 2.2.4. CARACTERISTICAS DE LA DISTRIBUCIÓN NORMAL L a curva normal es conocida como campana de gauss en honor al matematico Karl Gauss. Es muy aplicable en inferencia estadística. 9 Se ajusta aproximadamente a las distribuciones de frecuencias reales observadas. Es simetrica respcto a la media, µ. La media, la mediana y la moda son iguales. El area total debajo de la curva y por encima del eje X es igual a una unidad cuadrada. Si se levantan perpendiculares a una distancia de una desviación estandar a ambos lados de la media, se habra delimitando aproximadamente el 68.26% del area total. La curva normal es simetrica. 2.2.5. FORMULAS DE LA DISTRIBUCION NORMAL е = constante matematica con valor aproximado de 2.71828 ᴨ = constante matematica con valor aproximado de 3.14159 µ = media de la población σ = desviación estandar de la población 10 2.2.6. DISTRIBUCIÓN NORMAL O GAUSSIANA Está caracterizada por dos parametros: la media, µ y la desviación tipica, σ. Su función de densidad es: La curva normal adopta n nmero infinito de formas, determinadas por sus parametros µ y σ. 11 2.2.7. CURVA NORMAL Gran número de distribuciones tienen la forma de una campana; es decir, alejándonos de la media, a derecha e izquierda, el número de observaciones decrece de forma similar. Esto genera una curva simétrica. Se estudió su ecuación, resultando en función de la media y desviación típica de la distribución. Ante las infinitas posibles medias y desviaciones, nos encontramos con una infinidad de posibles distribuciones normales, pero, el proceso de tipificación, permite reducirlas a una única con media 0 y desviación típica 1. Tal distribución se denomina normal tipificada y se representa N (0,1). En términos de probabilidad, definimos igualmente la variable aleatoria normal, como aquella que tiene por gráfica de su función de densidad la representada a la izquierda. El área bajo la curva será igual a la unidad y, con este criterio se confeccionaron tablas estadísticas que calculan el área para un cierto intervalo de valores de la variable. Recordemos pues que la curva normal: a) es simétrica respecto a la media b) se establece que el área bajo su gráfica es igual a 1. Consecuencia de ello es, por ejemplo, que el área a la derecha de la media (o a la izquierda es 0'5) y que el área desde la media a un valor –V coincide con el área desde la media a V. 12 2.2.8. TIPIFICACIÓN MANEJO DE TABLAS Se ha indicado que los valores de las áreas bajo la curva normal se encuentran tabulados con referencia a la distribución normal tipificada N (0,1). Por ello, nos veremos obligados a tipificar previamente cualquier otro tipo de distribución normal que deseemos estudiar. Recordemos el procedimiento de tipificación: Suelen utilizarse dos tipos de tablas: Proporcionan el área a la izquierda. de un valor. Ofrecen el área comprendida entre la media (0) y un valor. En los dos casos, la tabla fija en la primera columna el valor de z con una cifra decimal y, la segunda cifra decimal de z condiciona la columna que ha de seleccionarse. En el cruce encontramos el área buscada. 13 2.2.9. EJERCICIOS 1. El tiempo promedio en que un estudiante tarda en llegar a la universidad es de 35 minutos, con una deviación estándar de 10 minutos. μ=35 min σ = 10 min Preguntas: a) ¿Qué porcentaje llega entre 35 y 50 minutos? b) ¿Qué porcentaje de estudiantes llegan entre 18 y 41 minutos? c) ¿Qué porcentaje de los estudiantes llegan en más de 28 minutos? Desarrollo: a) Z X 3 = 50 35 1.5 10 5 43.32% 14 b) 1 Z X = 3 18 35 1.7 10 4 Z + Z = 45.54% X = 41 35 0.6 10 Z = 22.57% Z = 68.11% c) 2 Z X = 3 28 35 0.7 10 25.8% + 15 50.0% CONCLUSIÓN Podemos concluir que hay una familia de distribuciones con una forma común, diferenciadas por sus valores de su media y de su varianza. También podemos decir que la distribución normal es la más usada en la probabilidad y la estadística, dado a que muchas poblaciones numéricas tienen distribuciones que se ajustan con precisión a una curva normal. El teorema central del límite nos permite aproximar la distribución binomial en una distribución normal. La distribución normal es importante porque nos permite con su fórmula transformar un valor de una distribución normal en una unidad de desviación estándar. Para comprender mejor la distribución normal planteamos su descubrimiento, en un pequeño grafico que nos encontramos midiendo la distancia y cada distancia no puede ser iual a la anteriormente tomada pues cometemos errores de medición ya sea por nosotros oh por los instrumentos que usamos al medirla, teóricamente un error puede ser tan grande que la distancia observada sea más infinita y también teóricamente menos infinito. Se plasman gráficos y sobre su eje se observa lo que realizamos en cada medición, canto más observamos las diversas mediciones que se realizan a un objeto para un gráfico podemos notar que esta va tomando forma de campana en el cuadro de mediciones realizadas. En un gráfico planteado al calcular la expresión analítica de dicha forma. 16 BIBLIOGRAFIA 1. Francisco Álvarez González francisco.alvarez@uca.es 2. https://www.bing.com/search’q= 3. www.gra.norm//distacia.ge 4. //graficoss.ejercicios.dedistnorm.com 5. Libro “MATEMATICA I”, (UNAP)…Autores: HAROLDO MONTOYA, MARCIAL MOLINA, JANDERY J. REVILLA GRANDEZ. VICTOR PRADO MENDOZA, JULIO IVAN MAYTAHUARI PACAYA. 6. Libro “Ciencias sociales, distancias y estadísticas”. 17 ANEXO 18 ANEXO N° 1 19 ANEXO N° 2 20