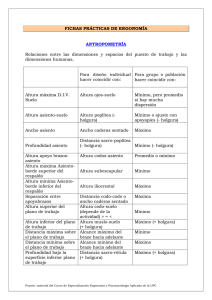
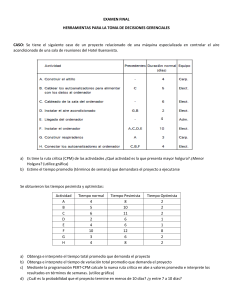
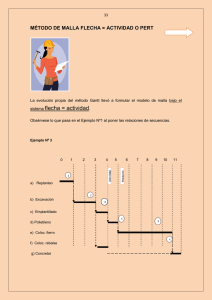
Ejercicio Resuelto: Programación Lineal con Simplex
Anuncio
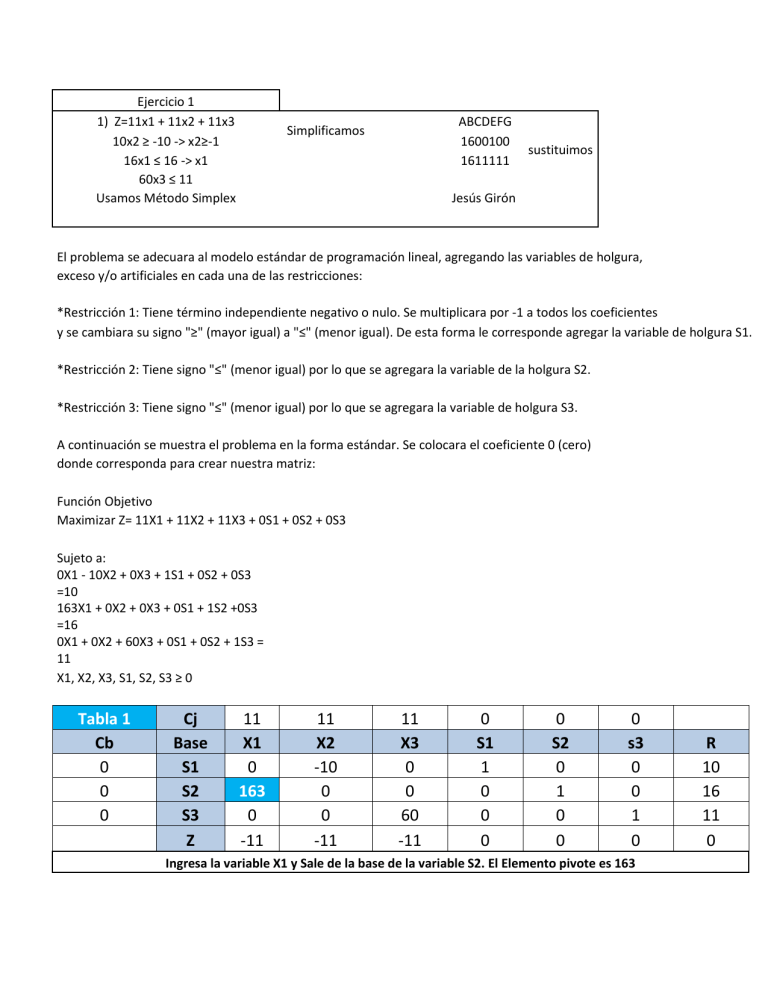
Ejercicio 1 1) Z=11x1 + 11x2 + 11x3 10x2 ≥ -10 -> x2≥-1 16x1 ≤ 16 -> x1 60x3 ≤ 11 Usamos Método Simplex ABCDEFG 1600100 1611111 Simplificamos sustituimos Jesús Girón El problema se adecuara al modelo estándar de programación lineal, agregando las variables de holgura, exceso y/o artificiales en cada una de las restricciones: *Restricción 1: Tiene término independiente negativo o nulo. Se multiplicara por -1 a todos los coeficientes y se cambiara su signo "≥" (mayor igual) a "≤" (menor igual). De esta forma le corresponde agregar la variable de holgura S1. *Restricción 2: Tiene signo "≤" (menor igual) por lo que se agregara la variable de la holgura S2. *Restricción 3: Tiene signo "≤" (menor igual) por lo que se agregara la variable de holgura S3. A continuación se muestra el problema en la forma estándar. Se colocara el coeficiente 0 (cero) donde corresponda para crear nuestra matriz: Función Objetivo Maximizar Z= 11X1 + 11X2 + 11X3 + 0S1 + 0S2 + 0S3 Sujeto a: 0X1 - 10X2 + 0X3 + 1S1 + 0S2 + 0S3 =10 163X1 + 0X2 + 0X3 + 0S1 + 1S2 +0S3 =16 0X1 + 0X2 + 60X3 + 0S1 + 0S2 + 1S3 = 11 X1, X2, X3, S1, S2, S3 ≥ 0 Tabla 1 Cb 0 0 0 Cj Base S1 S2 S3 Z 11 X1 0 163 0 -11 11 X2 -10 0 0 -11 11 X3 0 0 60 -11 0 S1 1 0 0 0 0 S2 0 1 0 0 0 s3 0 0 1 0 Ingresa la variable X1 y Sale de la base de la variable S2. El Elemento pivote es 163 R 10 16 11 0 Tabla 2 Cb 0 11 0 Cj Base S1 X1 S3 Z 11 X1 0 1 0 0 11 X2 -10 0 0 -11 11 X3 0 0 60 -11 0 S1 1 0 0 0 0 S2 0 1/163 0 11/163 0 s3 0 0 1 0 R 10 16/163 11 176/163 El problema tiene solución ilimitada (no acotada), La variable X2 debe entrar a la base pero ninguna variable puede salir.