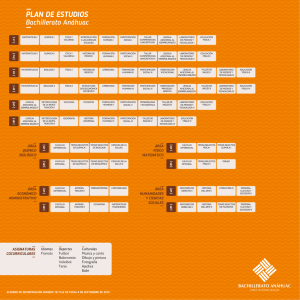
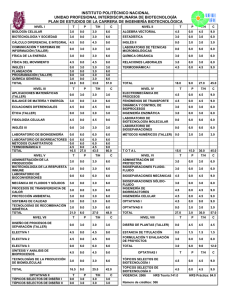
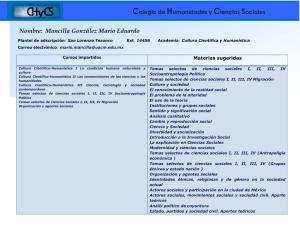
1 Tópicos Selectos de Transferencia de Masa INTRODUCCIÓN En la transferencia de masa el término coeficiente de difusión es utilizado para el trasporte molecular de masa que ocurre usualmente por un gradiente de concentración, pero en ocasiones es debido a un gradiente de temperatura, presión o por la acción de alguna fuerza impulsora. Está es una propiedad del sistema que depende tanto de la temperatura y la presión, como de la naturaleza de los componentes y se determina por medio del modelo matemático planteado por Fick en su primera ley. Las expresiones empíricas para calcular el coeficiente de difusión se utilizan cuando se tienen datos experimentales; teniendo en cuenta que para mezclas binarias de gases, estas ecuaciones están basadas en la teoría cinética de los gases y no dependen de la composición de la mezcla pero si son inversamente proporcionales a la presión y se incrementan con el aumento de la temperatura En este trabajo se mencionan las diferentes correlaciones empíricas para el cálculo del coeficiente de difusión a bajas y altas presiones. 2 Tópicos Selectos de Transferencia de Masa PREDICCION DEL COEFICIENTE DE DIFUSION PARA SISTEMAS GASEOSOS BINARIOS Y DE MEZCLAS MULTICOMPONENTES. 1. Coeficiente de Difusión El término coeficiente de difusión o difusividad es una propiedad del sistema que depende de la temperatura, presión y de la naturaleza de los componentes; suele emplearse como una medida de la tasa de transferencia de masa en ausencia de mezcla, ya sea mecánica o convectiva. Las expresiones para calcular la difusividad cuando no se cuenta con datos experimentales, están basadas en la teoría cinética de los gases, sin embargo en la etapa de pregrado se utilizan en alto grado los cálculos empíricos, los cuales cuentan con una gran exactitud pero dependen de los datos experimentales. En este trabajo solo se tendrán en cuentan los métodos de cálculo empíricos para determinar el coeficiente de difusión. 2. Cálculo del coeficiente de difusividad El coeficiente de difusividad es función de la temperatura y presión tal como lo es la viscosidad y la conductividad térmica que son las propiedades usadas en cantidad de movimiento y transferencia de calor respectivamente. Para una mezcla binaria, gaseosa a baja presión se encuentra que: Si p ↓ => DAB ↑ Si T ↑ => DAB ↑ Si xi ↑ o xi ↓ => DAB ≈ constante Para el cálculo del coeficiente de difusividad se han propuesto diversas correlaciones dependiendo de la fase, del intervalo de presión y/o temperatura en la que se encuentre el sistema. De la siguiente ecuación: N B N A N B C B D AB dC B C dz 3 Tópicos Selectos de Transferencia de Masa N A N B Se aplica al caso de la difusión en el sentido z únicamente, con y constantes (estado estacionario), las variables se separan fácilmente y si D AB es constante, se puede integrar: CA 2 N C A1 d c c C A ( N A N B) A 1 z2 c D AB z1 dz CA En donde el 1 indica el principio de la trayectoria de difusih ( CA el 2 el final de la trayectoria de difusih ( 1 ln NA NB N N c C A2 ( N A N B) A c C A1 ( N A N B) A N A D AB RTZ z1 z2 bajo). Sea elevado) y - =z z C D AB (1) ( PA1 PA2 ) (2) Cuando se puede aplicar la ley de los gases ideales, la ecuación (1) puede escribirse de manera más adecuada para su uso con gases. Entonces Pt PA2 PA1 ; En donde PA = presión parcial del componente A Pt =presión total yA =concentración de fracción de molar ADEMÁS: 4 Tópicos Selectos de Transferencia de Masa C P n t V RT De tal forma que la ecuación (2) se convierte en N A N /( )]P PA2 P [ D AB t ln N A N A N B t N A N B RTZ [ N A / ( N A N B)]Pt PA1 A (3) NA N /( )] y A 2 P [ D AB t ln N A N A N B N A N B RTZ [ N A / ( N A N B)] y A1 A (4) N A N B Para utilizar estas ecuaciones, debe conocerse la relación entre y . Ésta generalmente se fija por otros motivos. Por ejemplo, si se va a fraccionar metano sobre un catalizador, CH 3 C 2 H 2 CH 3 En circunstancias tales que el (A) se difunda hacia la superficie de H2 fraccionamiento y el (B) se difunda al seno del fluido, entonces la N B 2 N A estequiometria de la reacción fija la relación N A N A N B ,y 1 En otras ocasiones, en ausencia de reacción química, la relación puede fijarse por razones de entalpía. En el caso de las operaciones puramente separacionales, se presentan con frecuencia dos casos. 2.1. Difusión en estado estacionario de A través del no difundente B 5 Tópicos Selectos de Transferencia de Masa Esto puede suceder, por ejemplo, si se fuera a absorber amoniaco (A) del aire (B) en agua. Puesto que el aire no se disuelve apreciablemente en agua y si no se toma en cuenta la evaporación del agua, en la fase gaseosa sólo se difunde el amoniaco. Entonces, N B N A = 0, N A NB N A NB = const., 1 De la ecuación (3): N A D P AB t RTZPBM ( PA1 PA 2 ) PB 2 PB1 PA2 PA1 ; Pt PA2 PA1 ; PB 2 PB1 PA2 PA1 ; Puesto que entonces PB 2 PB1 PBM ln( PB 2 / PB1 Sea: PB 2 PB1 PBM ln( PB 2 / PB1 ) Entonces: N A D P AB t RTZPBM ( PA1 PA 2 ) Esta ecuación se muestra gráficamente en la figura 2.3. La sustancia A se difunde debido a su gradiente de concentración, - dp,/dz. La sustancia B también se difunde con relación a la velocidad molar promedio con un flux JB que depende de - dp/dz, pero al igual que un pez que nada a contracorriente a la misma velocidad que el agua que fluye con la corriente, Na = 0 relativo a un lugar fijo en el espacio . 6 Tópicos Selectos de Transferencia de Masa 2.2. Contradifusión equimolar en estado estacionario Esta es una situación que se presenta con frecuencia en las operaciones de destilación. N A NB const. N A PA D AB dPA Pt RT d z (N A NB ) O para este caso N A dP D AB A RT d z D z2 PA 2 dz RTN dP A A PA1 z1 N AB A D AB RTZ ( PA1 PA2 ) 7 Tópicos Selectos de Transferencia de Masa 2.3. Coeficiente de difusión para Sistemas Multicomponentes Las expresiones para la difusión en sistemas multicomponentes se vuelven muy complicadas, pero con frecuencia se pueden manejar utilizando una difusividad efectiva, en donde la difusividad efectiva de un componente puede obtenerse a partir de sus difusividades binarias con cada uno de los otros componentes. Así en estas ecuaciones N A NB se puede reemplazar n N i A N i i por donde es positivo si la difusión es en la misma dirección que A y negativo si es en la dirección opuesta; N N * D C ln N N z N N N C A2 A n A, m A A T i A i i A A n i A T C A1 n i C i C T n N i A i 0 8 Tópicos Selectos de Transferencia de Masa N P P N P N * D * ln N z RT N P N P N A A2 n A, m A i i A n A A i i A A1 n n N i i A N y N * D * P ln N N z RT N y N N i A i 0 i 0 A n A, m A i A n A A i i A n D A, B n i A D i A efectiva Ni N A,m Puede reemplazarse por la D A,m n A1 i i A D A2 i 1 D (y A ,i n y N A i i A N A y i A N) i D A ,i A, m Los son las difusividades binarias. Esto indica que puede variar considerablemente de uno de los lados de la trayectoria de difusión al otro, empero, generalmente se puede suponer una variación lineal con la distancia, par realizar cálculos prácticos. Una situación bastante común es N A que todas las N excepto sean cero, es decir, cuando todos los componentes, excepto uno, estén estancados, entonces la ecuación anterior se transforma: D A, m y y D 1 A n i B i A, i 1 y D n iB , i A ,i 9 Tópicos Selectos de Transferencia de Masa y , i Donde es la fracción mol del componente i, libre de A. y , i y 1 y i A Ejemplo 1: Calcular la rapidez de difusión del oxígeno (A) gas que no se está difundiendo es una mezcla de metano (B) e hidrógeno (C) en la relaci6n en 5 volumen 2:1. La presión total es 10 N m2 , y la temperatura es 273 K. La presión parcial de oxígeno en dos planos separados por 2.0 mm es, N 2 m . Se ha calculado que las respectivamente, 13 000 y 6 500 difusividades son: D O −H =6.99∗10 2 −5 2 m2 s , m2 D O −CH =1.86∗10 s −5 2 4 Solución: P P P T P A1 P B1 5 B1 10 1300 B1 87000 N m 2 P P P T P A2 P B 2 5 B2 10 6500 B2 93500 N m 2 10 Tópicos Selectos de Transferencia de Masa P B,M P B ,2 P B ,1 ln( P B ,2 ) P P B,M B ,1 (93500 87000) 90210.97 N 2 93500 m ln( ) 87000 z 0.002m R 8314 N .m y , y , B C kmol.K 2 0.667 2 1 1 0.667 0.333 D A, m D A, m 1 y D , B AB y D 0.667 2.46*10 m 5 A C AC 1 1.86*10 N , 5 2.46*10 0.333 6.99*10 5 m 2 s 5 2 *(13000 6500) s 3.91 kmol 2 8314* 273*0.002*90210.97 m s 2.4. Difusividad de gases a baja presión 11 Tópicos Selectos de Transferencia de Masa 2.4.1. Difusividad en mezclas gaseosas a baja densidad En gases, la difusividad aumenta con la temperatura, y disminuye al aumentar la presión. También disminuye al aumentar el peso molecular. En un gas a baja presión, la difusividad es independiente de la concentración, por lo que si se cumple que: DAB DBA Para la predicción de la difusividad en gases se han planteado diferentes modelos a partir de diferentes teorías, como la teoría cinética clásica, la teoría cinética de Chapman y Eskog, y teorías de estados correspondientes. a. Difusividad mediante la ley de estados correspondientes En esta ecuación los parámetros tienen las siguientes unidades D AB= cm2 s M= g mol T =° K P=atm A y B son constantes y esos valores están determinados para los siguientes casos: • Para gases no polares a=2.74 x 10−4 • b=1.823 Para el agua (H2O) y un gas no polar a=3.640 x 10−4 b=2.334 En el caso de que solo tuviéramos datos de la Difusividad a una T1 y P1 y quisiéramos calcular la Difusividad para una condición (2) que es T2 y P2. 12 Tópicos Selectos de Transferencia de Masa D AB 2 A , T 2 y P 2 Dato experimental D AB 2 A , T 1 y P 1 b T2 =a ( ) ( 1) 1 1 T CA T CB 1 1 1 /2 √ 3 4 ( PCA ) ( PCB ) (T CA ) ( T CB ) ( + ) MA MB D AB 2 . P2 b T1 =a ( ) ( 1) 1 1 1 /2 T T 1 1 √ CA CB ( PCA ) ( PCB ) 3 (T CA ) ( T CB ) 4 ( + ) MA MB D AB 1 . P1 Dividiendo (1) / (2) tenemos: D AB 2 . P 2 T 2 b =( ) D AB 1 . P 1 T 1 T 2 b P1 D AB 2=D AB 1 . ( ) T 1 P2 ( ) Grado de error de esta ecuación es de 5% y 19% El comportamiento de esta ecuación no es muy buena a presiones altas. Tabla B.1 parámetros críticos → Bird. Ejemplo 2: Se tienen los siguientes datos: b=2 D AB 1=13 x 10 −2 cm2 s D AB 2=? 13 Tópicos Selectos de Transferencia de Masa T 1 =273° k T 2 =283° k P1=1 atm T 2 =8 atm Calculamos: T D AB 2=D AB 1 . 2 T1 b P1 cm 2 1 atm 283 ° K 2 =13 x 10−2 ( )( ) P2 s 8 atm 273 ° K ( )( ) D AB 1=0.01746 λ= cm 2 s 1 Caminolibre medio( N numero de particulas por unidad de volumen) √2 π σ 2 N ¿ v =c= √ 8 RT Velocidad cinetica media de las p articulas πM ¿ 1 N z= v Numero de particulas que chocan contrauna superficie 4 N0 Ejemplo2: Se esparce en un cuarto un gas en el suelo, hipoclorito de calcio, para que libere cloro 14 Tópicos Selectos de Transferencia de Masa (τ) Distancia entre los centros de las partículas λ = (Camino libre medio) distancia promedio entre dos colisiones sucesivas XA Fracción molar del componente A (componente cloro) desprendido XA ≈ Alta concentración de cloro en el piso casi al 100% (a) Distancia entre planos imaginarios XA y Concentración del cloro a una distancia (y) XA y −a Concentración del cloro a una distancia (y-a) XA y+a Concentración del cloro a una distancia (y+a) 15 Tópicos Selectos de Transferencia de Masa Ejemplo 3: La partícula se desplaza y recorre una distancia a1, a2, a3…….. en promedio la distancia es menor (λ). Si tuviese que recorrer más que (λ) chocara con otra partícula para poder chocar con el plano. a= a1+ a2 +a3 +… …+ an n a = Distancia promedio que recorre la partícula después de chocar con otra hasta un plano imaginario hasta un choque. SI a ≠ λ No es choque entre moléculas si que es choque con el plano imaginario. Si a > λ Antes de chocar con el plano choca con una partícula y luego con el plano. Si a = λ Choca con una partícula en el aire. Por definición: 2 a= λ De maneraexperimental 3 Analizando la figura 4: 16 Tópicos Selectos de Transferencia de Masa XA X = A y −a y +b XA X = A y + a y−b Con ayuda de la pendiente del complemento del ángulo β m=tanβ = dy d XA tanα=−tan ( 180−β ) = −dy a = d XA b tanα= a b Despejando (b): b= b= a dy d XA −2 d X A λ 3 dy Reemplazando en (1) y en (2) tenemos: 2 d XA X A / y−a=X A / y− λ 3 dy 2 d XA X A / y+ a= X A / y + λ 3 dy −dy a = dXA b 17 Tópicos Selectos de Transferencia de Masa GMA = N¿ v. XA/ y N0 N = Conjunto de moléculas que atraviesan el plano por unidad de volumen (Cl2 + Aire) o también de moles unidad de volumen. N0 = Concentración total GMA = N¿ 1 N¿ 1 N¿ V . X / y + v X / y−a− v X / y+a A A 4 N0 4 N0 A N0 N¿ v flujo de lacorriente( flujo molar total ) N0 G MA = N¿ 1 N¿ 2 d XA 2 d XA v . X / y + v 0 (X A / y− λ −X A / y− λ ) A 0 4 N 3 dy 3 dy N 1 N¿ v . X A / y−a particulas que chocan haciaarriha 4 N0 Ecuación del flujo cuando el cloro se mueve a través del aire N 1 N dXA GMA = 0 v . X A / y − v 0 λ 3 N dy N ¿ 1. ¿ Comparando esta ecuación con la ley de Fick para el ejemplo: 2.G MA =(G MA +G MB) X A −C D AB Movimiento del cloro y del aire) (Movimiento individual del cloro) Las ecuaciones 1 y 2 son semejantes C D AB d X A 1 N¿ d X A = v 0λ dy 3 N dy d XA dy 18 Tópicos Selectos de Transferencia de Masa ¿ N =C 0 N C D AB d XA 1 d XA = vCλ dy 3 dy 1 D AB= vλ 3 v Velocidad media de las partículas v= √ 8 RT πM 1 D AB= vλ 3 D AB= √ 1 8 RT 1 . 3 πM √ 2 π σ 2 N ¿ De la ecuación de gases generales PV =nRT PV = N ¿= D AB= √ 1 8 RT . 3 πM 3/ 2 2 R D AB= ( ) 3 π 1 √2 π σ 2 1 N0 √ P N0 RT 1 3 T M P σ2 N RT 0 N N PN0 = V RT 19 Tópicos Selectos de Transferencia de Masa Esta ecuación se usa cuando v y λ Son resultado de la teoría cinética: cuando las partículas son esféricas, cuando las partículas son iguales cuando se trata de mezclas. D AB=1.8583 x 10−3 √ ( 1 1 + ) T3 M A MB σ 2 AB P Ω AB Ecuación para calcular la difusividad en estados correspondientes cuando no hay fuerzas de atracción y repulsión (ecuación error del 5%) En tablas del libro Bird se tiene el ε A y ε B , σ A y σB Parámetros: σ AB = σ A +σ B ( EN TABLAS B−1) 2 ε AB =√ ε A . ε B ( Energia maximade atraccion molecular) En el caso de que solo tuviéramos datos de la Difusividad a una T1 y P1 y quisiéramos calcular la Difusividad para una condición (2) que es T2 y P2. D AB 2=1.8583 x 10−3 √ ( 1 1 + )T 32 MA MB ( 1) σ 2 AB P2 Ω AB 2 20 Tópicos Selectos de Transferencia de Masa D AB 2=1.8583 x 10−3 √ ( 1 1 + )T 31 MA MB (2) σ 2 AB P1 Ω AB 1 Dividiendo (1) y (2) tenemos: 3 P T Ω D AB 2=D AB 1 ( 1 ) 2 2 ( DAB 1 ) P 2 T 1 ΩDAB 2 ( ) Para hallar D AB calculamos KT ε AB pero ε AB no hay en tablas (B-2) y (B-1) Entonces: εA K y εB K hay en tablas √ ε AB ε ε = A. B K K K La difusión en gases alta densidad significa que la presión es mayor a los 10 Atm. (P>10Atm.). Alta densidad P > 10 atm PC =Presion pseudo critica 21 Tópicos Selectos de Transferencia de Masa T C =Temperatura pseudo critica Parámetros reducidos están en función de la composición se puede utilizar para cualquier mezcla gaseosa. π= τ= P Pc T Tc P D AB ( P D AB)0 =α El numerador de esta relación es el producto de la presión alta por la difusividad a una temperatura cualquiera, y el denominador es el producto de una presión baja o multiplicada por la difusividad a la presión baja y a una temperatura igual a la difusividad del numerador. b. Modelo de la teoría cinética de CHAPMAN-ENSKOG DAB 0.0026627T 1.5 0.5 2 PM AB AB D Se basa en el modelo de Lennard-Jones para la energía potencial de interacción entre una molécula de A y una de B: AB 12 AB 6 AB (r ) 4 AB r r AB Donde (energía característica, que se suele usar dividida entre la AB constante de Boltzmann K ) y (diámetro de colisión) son parámetros 22 Tópicos Selectos de Transferencia de Masa que dependen de las moléculas que interactúan y se obtienen a partir de los valores de las sustancias puras: AB AB A B . K K K 1 A B 2 0.5 /K y son valores reportados y se recomienda que vengan de las misma fuente bibliográfica. Cuando no se tienen estos valores reportados, se pueden estimar con la temperatura y el volumen molar en el punto de ebullición normal: 1.15Tb K 1/3 1.166V° b D La integral de colisión se puede consultar tabulada en función de la temperatura adimensional T* T* , definida como: KT AB T* T AB / K o bien D A C E G * B * * (T ) exp( DT ) exp( FT ) exp( HT * ) Donde: A 1.060 B 0.156 C 0.19 D 0.476 E 1.03 F 1.52 G 1.76 H 3.89 Tabla 1. Parámetros de Leonard-Jones y otras propiedades 23 Tópicos Selectos de Transferencia de Masa 24 Tópicos Selectos de Transferencia de Masa Tabla 2. Integral de Colision (Leonnard-Jones) 25 Tópicos Selectos de Transferencia de Masa Ejemplo 4: Estime el coeficiente de difusion para la mezcla de CO 2-N2 a 590k y 1bar.Experimentalmente se ha reportado en 1872 una difusividad de 0.583 cm2/s. Solucion: Datos co2 3.941A N2 3.798 A CO2 N2 145.2 71.4 CO2 N 2 Hallamos CO2 N2 / k ( co2 N2 Hallamos CO2 N2 1/ 2 . ) (145.2 x 71.4)1/2 101.819 26 Tópicos Selectos de Transferencia de Masa co2 N 2 1 3.941 3.798 3.8695 A A B 2 2 Reemplazamos en la siguiente ecuación: T* T* T AB / K 590 5.7946 101.819 Hallamos el factor de coalición: D D A C E G * B * * (T ) exp( DT ) exp( FT ) exp( HT * ) 1.060 0.19 1.03 1.76 0.156 (5.7946) exp(0.476 x5.7946) exp(1.52 x5.7946) exp(3.89 x5.7946) D 0.8181 Finalmente remplazamos en la ecuacion para hallar la difusividad DAB DAB 0.0026627T 1.5 0.5 2 PM AB AB D 0.0026627(590)1.5 1(36)0.5 (3.8695) 2 0.8181 DAB 0.5192cm 2 / s c. Teoría modificada por BROKAV para gases polares Cuando uno o ambos de los gases son polares, se puede obtener mejores estimaciones de la difusividad. Esta modificación emplea la misma fórmula 27 Tópicos Selectos de Transferencia de Masa básica para calcular la difusividad pero los parámetros se obtienen de forma diferente: DAB 0.0026627T 1.5 0.5 2 PM AB AB D Primero es necesario calcular un parámetro polar adimensional en base al momento dipolo . Este parámetro se emplea luego para calcular la energía característica y el diámetro de colisión para cada una de los dos compuestos: 1940 2 V°bTb 1.18 1 1.3 2 Tb K 1.585V°b 2 1 1.3 1/3 AB / K La energía característica combinada y el diámetro de colisión AB combinado se calculan de la misma forma que en la Teoría Cinética de Chapman- Enskog. También se calcula un parámetro polar combinado AB A B 0.5 Se agrega una corrección a la integral de colisión: 2 D D (tabulada ) 0.19 AB Donde: AB / K T 28 Tópicos Selectos de Transferencia de Masa D (tabulada ) Es el valor obtenido de las tablas de datos. Finalmente, la difusividad se calcula empleando la misma ecuación del método de Chapman y Enskog. d. Método de FULLER D AB 10 9.T P A 1/ 3 1.75 1/ 3 2 B 1 MA 1 1/ 2 M B Donde: DAB: Difusividad (cm2/s) T: Temperatura (K) P: Presión (atm) V: Volumen atómico o molecular (cm3/mol) MA y MB: Pesos moleculares Los valores de se obtienen por contribución de grupos de acuerdo a la tabla siguiente. Para algunas moléculas simples se recomienda emplear los valores especiales indicados consecuentes. Tabla 3 Contribuciones de grupo para volúmenes moleculares de difusión (Método de Fuller) Tabla 4. Volúmenes Moleculares de difusión para algunas moléculas simples (Método de Fuller) 29 Tópicos Selectos de Transferencia de Masa Ejemplo 5: El vapor de cadmio es toxico. Determine la difusividad en aire a la presión de 1 atm y T=1038 k, v=14 cm3/mol para el cadmio , PM=112.4 gr/mol. Para el aire PM=29 gr/mol y V=20.1 cm3/mol Solución: Utilizamos la siguiente formula: D AB 1.75 10 9.(1038) 1 14 1/ 3 20.1 1/ 3 D AB 2 1 1 112.4 29 1/ 2 3.2929 x106 cm 2 / s e. Método de la extrapolación de HIRSCHFELDER Se emplea para estimar la difusividad a una cierta temperatura y presión cuando ya se tiene como dato la difusividad a otra temperatura y presión conocidas. 1.5 DAB T2 , P2 T P1 DAB T1 , P1 2 T1 P2 Cuando el rango de temperatura es grande, se necesita incluir también un factor adicional relacionando las integrales de colisión a ambas temperaturas: 1.5 DAB T2 , P2 T P1 DT1 DAB T1 , P1 2 T1 P2 D T2 Ejemplo 6: El coeficiente de difusión del CO2 en aire a 1 atm de presión y 400k es 2.63x10-5 cm2/s .Calcular La difusión de CO2 en aire a 600k y 5 atm. 30 Tópicos Selectos de Transferencia de Masa Solución Utilizamos la extrapolación de Hirschfelder 1.5 DAB T2 , P2 T P1 DAB T1 ,P1 2 T1 P2 1.5 600 1 400 5 DAB T2 , P2 2.63x105 cm 2 / s DAB T2 , P2 9.663x106 cm 2 / s 2.5. Difusividad en gases a alta presión No existe un valor específico de presión a partir del cual se considere "alta". Normalmente los métodos para gases a baja presión comienzan a mostrar desviaciones significativas a presiones de 5 atm o mayores. A diferencia de los gases a baja presión, a alta presión la difusividad sí depende de la composición. Los métodos para gases a alta presión generalmente requieren de datos a baja presión a la misma temperatura del sistema (indicado con un superíndice +). Esta baja presión suele ser presión atmosférica, aunque puede ser otra presión si ya se tienen datos a esa presión, pero todos esos datos deben ser a la misma presión. Normalmente se requieren también propiedades pseudocríticas de la mezcla ( ,c AB T , ,c AB P y AB ) para calcular propiedades reducidas. a. Método de estados correspondientes de TAKAHASHI +¿ (D AB P) =f ( T , P) D AB P ¿ 31 Tópicos Selectos de Transferencia de Masa La relación entre el producto D AB P y su correspondiente valor a baja presión (DAB P)+ está dado en función de las condiciones reducidas de acuerdo a la Figura 1. b. Método de RIAZI Y WHITSON μ+¿ μ ¿ ¿ ¿ (D AB P)+¿ =1.07 ¿ D AB P ¿ Para calcular la presión reducida r P se emplea la presión pseudocrítica de la mezcla, mientras que b y c son funciones del factor acéntrico de la mezcla WAB: B= -0.38 WAB - 0.27 c= 0.1W AB - 0.05 Este método falla para bajas presiones ya que no se obtiene el valor correcto de difusividad. Otra dificultad que presenta es que la viscosidad y la viscosidad a baja presión µ+ generalmente dependen también de la composición. 32 Tópicos Selectos de Transferencia de Masa 3. Conclusiones Estos métodos de cálculo son efectivos para tenerlos en cuenta a nivel estudiantil o para hacer simulaciones a nivel experimental ya que estos se basan en datos experimentales, los cuales no son tan confiables para tenerlos en cuenta en los cálculos de diseño de equipos a escala industrial. Estos métodos deben ser utilizados en la fase estudiantil ya que son de gran utilidad para comprender fenómenos de trasferencia de masa en procesos de separación no convencionales como destilación, absorción, extracción, etc. 4. Bibliografía ROBERT BIRD. Fenómenos de Transporte. Segunda Edición. México. ROBERT E. TREYBAL. Operaciones de Transferencia de Masa. Segunda Edición. 33 Tópicos Selectos de Transferencia de Masa S. Chapman y T. G. Cowling, The Mathematical Theory of Nonuniform Gases, Cambridge University Press, 3rd edition, 1970. J. H. Ferziger y H. G. Kaper, Mathematical Theory of Transport Processes in Gases, North-Holand, 1972.