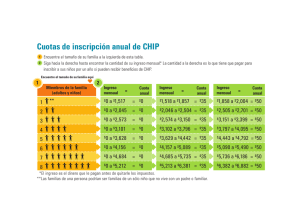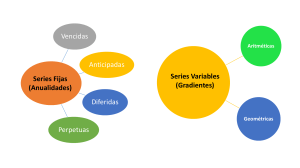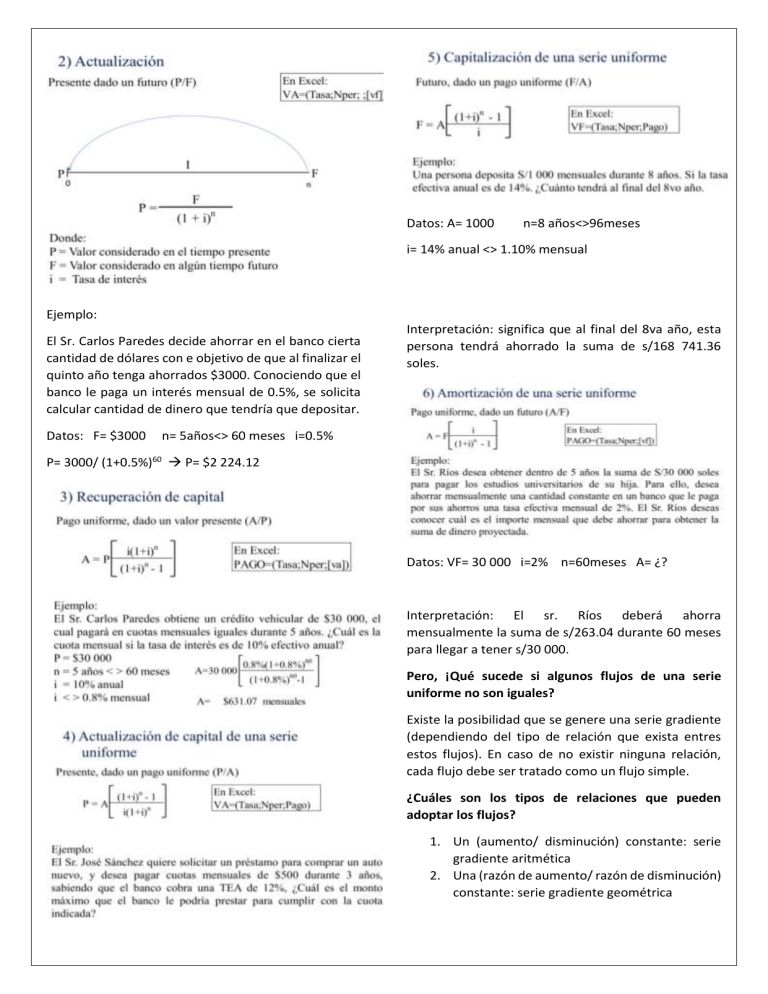
Datos: A= 1000 n=8 años<>96meses i= 14% anual <> 1.10% mensual Ejemplo: El Sr. Carlos Paredes decide ahorrar en el banco cierta cantidad de dólares con e objetivo de que al finalizar el quinto año tenga ahorrados $3000. Conociendo que el banco le paga un interés mensual de 0.5%, se solicita calcular cantidad de dinero que tendría que depositar. Datos: F= $3000 Interpretación: significa que al final del 8va año, esta persona tendrá ahorrado la suma de s/168 741.36 soles. n= 5años<> 60 meses i=0.5% P= 3000/ (1+0.5%)60 P= $2 224.12 Datos: VF= 30 000 i=2% n=60meses A= ¿? Interpretación: El sr. Ríos deberá ahorra mensualmente la suma de s/263.04 durante 60 meses para llegar a tener s/30 000. Pero, ¡Qué sucede si algunos flujos de una serie uniforme no son iguales? Existe la posibilidad que se genere una serie gradiente (dependiendo del tipo de relación que exista entres estos flujos). En caso de no existir ninguna relación, cada flujo debe ser tratado como un flujo simple. ¿Cuáles son los tipos de relaciones que pueden adoptar los flujos? 1. Un (aumento/ disminución) constante: serie gradiente aritmética 2. Una (razón de aumento/ razón de disminución) constante: serie gradiente geométrica TIPOS DE SERIES GRADIENTES ARITMÉTICAS ¿Qué sucede si necesita conocer la magnitud de determinado flujo de una serie gradiente geométrica? Ejemplo de determinación de termino n- ésimo para serie gradiente aritmética Dada la siguiente gradiente aritmética, determinar la magnitud del flujo que está en t=30. Ejemplo de determinación de termino n- ésimo para serie gradiente geométrica FORMACIÓN DE SERIE DE GRADIENTES ARITMÉTICAS Dada la siguiente gradiente geométrica, determinar la magnitud del flujo que está en t=60. ¿se puede el valor presente y el valor futuro de las series gradientes? Efectivamente, si, empleando as siguientes expresiones y teniendo en consideración que. TIPOS DE SERIES GRADIENTES GEOMETRICAS A Es importante el primer flujo de la serie gradiente G Es el numero para aritméticas y un % para geométrica i,n deben de coincidir en periocidad Se transforma la tasa, no el flujo, además n a cantidad de flujos que compone la serie gradiente La ubicación del valor presente es un periodo antes de inicio de la serie gradiente La ubicación del valor fututo es el ultimo periodo de la serie gradiente TABLAS DE AMORTIZACIÓN Deudas: “Solo hay dos medios para pagar las deudas, por el trabajo y por el ahorro” - Thomas Carlyle ¿Alguna vez te has preguntado como las entidades financieras calculan la cuota mensual de un préstamo que has solicitado o como las tarjetas de crédito calculan los diferidos con intereses de tus consumos? ¿Qué significa amortizar? En términos financieros, es la distribución gradual del costo de una deuda mediante pagos periódicos, estos pagos (cuotas) que incluyen intereses irán reduciendo el monto del préstamo hasta llegar a cero en el pago de la última cuota. ¿Qué es una tabla de amortización? Es un cuadro donde se muestra el calendario de pagos de un préstamo que se ha solicitado al banco. A continuación, se muestra un modelo de la tabla de amortización: Caso utilizando el método alemán Recordando que el método alemán, la amortización de capital constante y no la cuota como el método francés. Métodos: existen dos métodos más usados El método francés: bajo esta metodología se presume que las cuotas son constantes. El método alemán: bajo esta metodología se presume que la amortización del capital es constante. Variantes en ambos métodos: Periodo de gracia: a) Periodo de gracia parcial b) Periodo de gracia total Cuotas extras: a) Cuota adicional (entiéndase amortización de capital) b) Cuota múltiplo, que pueden se ejemplo, cuotas dobles, triples, etc. Caso con periocidad de gracia parcial (Método Francés): Recordar para hallar la anualidad (cuota constante), debemos tomar en cuenta 9 meses y no 10, por lo cual n=9, ya que en el mes 1, solo se paga intereses. Caso con cuota múltiplo (en este caso cuota doble) (Método Frances): Caso con periocidad de gracia total (Método Francés): Recordar para hallar la anualidad (cuota constante), debemos tomar en cuenta que el mes 1 se acumula en la deuda, por lo cual, el préstamo es s/ 20 200, y la anualidad se calcula tomando en cuenta que P= s/20 200. TASA DE COSTO EFECTIVA ANUAL Caso con cuota adicional (entiéndase amortización adicional) (Método Frances): como Debido a que hay cuota adicional (entiéndase en el caso amortización adicional), entonces traemos a valor presente todas las cuotas A + el importe adicional s/1000.