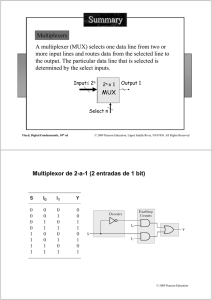
Machines and Mechanisms: Applied Kinematic Analysis, 4/e Chapter 1 Chap 1 Introduction Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 2 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 1.1 INTRODUCTION Determine appropriate movement of the wipers View range Tandem or opposite Wipe angle Location of pivots Timing of wipers Wiping velocity The force acting on the machine Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 3 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 1.2 MACHINES AND MECHANISMS Machine Devices used to alter, transmit, and direct forces to accomplish a specific objective Mechanism Mechanical portion of a machine that has the function of transferring motion and forces from a power source to an output Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 4 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 1.3 KINEMATICS Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 5 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Dynamics Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 6 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Kinematics Kinematics Kinematic analysis Determine Position, displacement, rotation, speed, velocity, acceleration Provide Geometry dimensions of the mechanism Operation range Dynamic analysis Deal with the way things move Power capacity, stability, member load Planar mechanism – motion in 2D space Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 7 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 1.4 MECHANISM TERMINOLOGY Mechanism Synthesis is the process of developing mechanism to satisfy a set of performance requirements for the machine. Analysis ensures that the mechanism will exhibit motion to accomplish the requirements . Linkage Frame Links– rigid body Joint Primary joint (full joint) Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 8 Revolute joint (pin or hinge joint)– pure rotation Sliding joint (piston or prism joint)– linear sliding © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Higher-order joint (half joint) Simple link A rigid body contains only two joints Crank Rocker Complex link Allow rotation and sliding Cam joint Gear connection A rigid body contains more than two joints Rocker arm Bellcrank Point of interest Actuator A power source link Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 9 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 1.5 Kinematic Diagram Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 10 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Kinematic Diagram Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 11 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 12 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 13 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 14 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 1.7 MOBILITY 1.7.1 Gruebler’s Equation Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 15 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Constrained mechanism Locked mechanism one degree of freedom Zero or negative degrees of freedom Unconstrained mechanism More than one degree of freedom Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 16 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 17 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 18 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 19 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Actuators and Drivers Electric motors (AC) Electric motors (DC) Engines Servomotors Air or hydraulic motors Hydraulic or pneumatic cylinders Screw actuators Manual 1.7.2 Actuators and Drivers Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 20 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 21 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 1.8 COMMONLY USED LINKS AND JOINTS 1.8.1 Eccentric Crank 1.8.2 Pin-in-a-Slot Joint 1.8.3 Screw Joint Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 22 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 23 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 1.9 SPECLAL CASES OF THE MOBILITY EQUATION 1.9.1 Coincident Joints 1.9.2 • One degree of freedom actually if pivoted links are the same size Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 24 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 25 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 1.10 THE FOUR-BAR MECHANISM Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 26 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 27 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 1.10.1 Degree-of-Freedom s : short link l : long link p , q : intermediate link Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 28 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 29 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 1.11 SLIDER-CRANK MECHANISM Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 30 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 1.12 SPECIAL PURPOSE MECHANISMS 1.12.1 Straight-Line Mechanisms Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 31 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 1.12.2 Parallelogram Mechanisms Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 32 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 1.12.3 Quick-Return Mechanisms Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 33 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 1.12.4 Scotch Yoke Mechanism Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 34 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e Chapter 4 Displacement Analysis 4.2 POSITION 4.2.1 Position of a Point 4.3 DISPLACEMENT 4.3.1 Linear Displacement 4.3.2 Angular Displacement Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 36 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 4.4 DISPLACEMENT ANALYSIS Locate the positions of all links as driver link is displaced Configuration Positions of all the links One degree of freedom Moving one link will precisely position all other links Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 37 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 4.5 DISPLACEMENT:GRAPHICAL ANALYSIS 4.5.1 Displacement of a Single Driving Link 4.5.2 Displacement of the Remaining Slave Links Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 38 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 4.5.2 Displacement of the Remaining Slave Links Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 39 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 40 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 41 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 4.1 Vector Analysis of Displacement Y1 Y r4 r2 r3 r3 r5 X1 r1 r4 X (1) r 1 r 2 r 3 r 4 0 r1s1 r2 c 2 r3c3 5.3 r c r s r s 3.2 0 1 1 2 2 3 3 r1 3,1 30,r2 4.9,r3 3.3 2 equations for 2 unknows 2 ,3 (2) r 3 r 4 r 5 0 r3c3 r4 c 4 x1 r s r s 0 3 3 4 4 0.8 r1 10.1 2 equations for 2 unknows 4 and x1 Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 42 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 43 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y r1 r2 r4 X r3 r 1 r 2 r 3 r 4 0 1.6 3c 2 r3c3 2.3 1.5 3s r s 0 0 2 3 3 r3 (3.92 1.22 )1/2 solve for 2 and 3 Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 44 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Analysis of Mechanism Position Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 45 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y r1 r2 r3 X r 1 r 2 r 3 0 50c1 40c 2 d1 50 s 40s 0 0 1 2 1 240,solve for 2 and d1 whenrotate15,1 255 50c1 40c 2 d 2 50 s 40s 0 0 1 2 solve for 2 and d 2 d d1 d 2 Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 46 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 47 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 4.6.1 Closed-Form Position Analysis Equations for an In-Line Slider-Crank Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 48 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 4.6.2 Closed-Form Position Analysis Equations for an Offset Slider-Crank Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 49 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 50 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y r2 r3 r1 r4 X r 1 r 2 r 3 r 4 0 12c1 20c 2 15c3 25 12s 20s 15s 0 0 1 2 3 1 90,eqs.solve for 2 and 3 1 60,eqs.solve for 2 and 3 Calculate the difference of 2 inand Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 51 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 52 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y r1 X r3 r2 r 1 r 2 r 3 0 0.5c1 1.75c 2 1 0.5s 1.75s y 0 1 2 for1 2 ,solve for1and ymax for1 2 ,solve for1and ymin Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 53 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 4.7 LIMITING POSITIONS: Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 54 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y r1 X r2 r4 r3 r 1 r 2 r 3 r 4 0 for1 2 ,solve for1and 3 )max for1 2 ,solve for1and 3 )min Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 55 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y r1 X r4 r2 r3 r 1 r 2 r 3 r 4 0 for 2 3 ,solve for1 max and 2 for 2 3 ,solve for1 min Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 56 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 4.9 TRANSMISSION ANGLE Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 57 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y X r3 r1 r2 r 1 r 2 r 3 r 4 0 0.5c1 lc 2 2.0 0.5s ls 0 0 1 2 given1solve forland 2 Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 58 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y r 1 r 2 r 3 0 r2 x r1 30,r2 70,r 3 0 30 given1 solve for 2 and x r3 r1 Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka X 59 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e Chapter 6 Velocity Analysis 6.2 LINEAR AND ANGULAR VELOCITY 6.2.2 Linear Velocity of a General Point Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 61 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. VA cos VB along ABlink wAB VA sin /(link length) Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 62 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y r1 X r2 r4 r3 r 1 r 2 r 3 r 4 0 2 r 2 3r 3 4 r 4 0 eqs forunknowns3 and 4 Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 63 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 6.6 GRAPHICAL VELOCITY ANALYSIS:RELATIVE VELOCITY METHOD 6.6.1 Points on Links Limited to Pure Rotation or Rectilinear Translation 6.6.2 General Points on a Floating Link Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 64 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y X r1 r4 r3 r2 r 1 r 2 r 3 0 0 1r 1 2 r 2 0 5 eqs for1and 2 r r 1 r 4 r 1r 1 2 r 4 Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 65 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y r1 r2 X r3 r 1 r 2 r 3 0 solve forand 1r 1 2 r 2 r2 0 vc 2 1 5rad min,r 2 vs 2 eqs forunknowns2 and v Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 66 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y X r1 r2 r3 r 1 r 2 r 3 0 1r 1 2 r 2 r2 0 0 r 2 50 eqs forunknowns1and 2 Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 67 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. r2 r1 Y r3 X r 1 r 2 r 3 0 1 r2 6, 2 340 r 3 3 eqs forunknownsr1and 1 1r 1 2 r 2 r 2 0 8c 2 r 2 8s 2 eqs forunknowns1and 2 Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 68 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 6.9 ALGEBRAIC SOLUTIONS 6.9.1 Slider-Crank Mechanism Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 69 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 6.9.2 Four-Bar Mechanism Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 70 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 6.10 INSTANTANEOUS CENTER OF ROTATION Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 71 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 6.11 LOCATING INSTANT CENTERS 6.11.1 Primary Centers Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 72 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 6.12 GRAPHICAL VELOCITY ANALYSIS: INSTANT CENTER METHOD Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 73 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y X r1 r2 r4 r3 r 1 r 2 r 3 r 4 0 1r 1 2 r 2 3r 3 0 given3 solve for1and 2 Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 74 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y r3 r2 r4 r 1 r 2 r 3 r 4 0 r1 r4 r6 X 2 r 2 3r 3 4 r 4 0 2 60rpm.solve for3 and r 4 r 5 r 6 0 r5 0 4 r 4 5 r 5 0 v eqs forunknowns5 and v Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 75 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y r2 r1 r3 X r4 r 1 r 2 r 3 r 4 0 1r 1 2 r 2 3r 3 0 given 1 find 2 and 3 Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 76 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e Chapter 7 Acceleration Analysis 7.2 LINEAR ACCELERATION 7.2.1 Linear Acceleration of Rectilinear Points Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 78 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y X r1 r2 r4 r3 r 1 r 2 r 3 r 4 0 1r 1 2 r 2 3r 3 0 given 1 find 2 and 3 1 1r 1 2 2 2 r 2 3 3 3r 3 0 solve for2 and 3 Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 79 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. r5 rp rp r 1 r 2 r 3 r 5 0 rp 1r 1 2 r 2 3 r 3 r 5 rp Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 80 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y X r1 r2 r3 r 1 r 2 r 3 0 0 1r 1 2 r 2 0 v solve for2 and v 0 1 1 1r 1 2 2 2 r 2 0 a solve for2 and a Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 81 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 82 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 7.8 ALGEBRAIC SOLUTIONS 7.8.1 Slider-Crank Mechanism Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 83 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 7.8.2 Four-Bar Mechanism Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 84 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y r3 r2 X r1 Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 85 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 7.10 ACCELERATION IMAGE ( Useless! ) Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 86 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 7.11 CORIOLIS ACCELERATION Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 87 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Y r2 r3 X r1 r 1 r 2 r 3 0 solve for1and 2 1r 1 r 2 2 r 2 0 vc 1 400,r 2 2 ,solve for2 and v vs 2 ac 1 1r 1 2 2 2 r 2 2 0 as 2 solve for2 and a Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 88 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 7.12 EQUIVALENT LINKAGES Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 89 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e Chapter 9 Cams 9.1 INTRODUCTION Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 91 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Plate cam Cylindrical cam Linear cam Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 92 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 9.2 TYPES OF CAMS Follower motion Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 93 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Follower position Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 94 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 9.3 TYPES OF FOLLOWERS Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 95 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 9.11 THE 4-STATION GENEVA MECHANISM Constant rotation producing index motion Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 96 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e Chapter 13 STATIC FORCE ANALYSIS 13.3 MOMENTS AND TORQUES Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 98 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 13.5 FREE-BODY DIAGRAMS 13.5.1 Drawing a Free-Body Diagram 13.5.2 Characterizing Contact Forces Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 99 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 13.6 STATIC EQUILIBRIUM Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 100 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. 13.7 ANALYSIS OF A TWO-FORCE MEMBER Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 101 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 102 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e Chapter 14 DYNAMIC FORCE ANALYSIS Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 104 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved. Machines and Mechanisms: Applied Kinematic Analysis, 4/e David Myszka 105 © 2012, 2005, 2002, 1999 Pearson Higher Education, Upper Saddle River, NJ 07458. • All Rights Reserved.