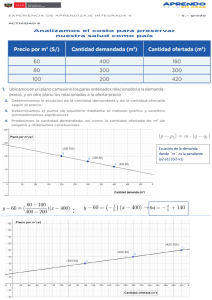
Tipos de control P, I, D, PI, PD, PID Ingeniería de Control Unidad II Controladores Por Francisco Javier Ramírez Ruiz Febrero 2021 Efecto en la adición de polos (Hernández, 2010) Efecto en la adición de ceros Control proporcional: P (Hernández, 2010) Se dice que un control es de tipo proporcional cuando la salida del controlador v(t) es proporcional al error e(t): 𝑣 𝑡 = 𝐾𝑝 𝑒 𝑡 Que es su equivalente en el dominio s: 𝑉 𝑠 = 𝐾𝑃 𝐸(𝑠) ∴ 𝑉(𝑠) 𝐺𝑐 𝑠 = 𝐸(𝑠) = 𝐾𝑃 Control integral I (Hernández, 2010) Se dice que un control es de tipo integral cuando la salida del controlador v(t) es proporcional a la integral del error e(t): 𝑣 𝑡 = 𝐾𝑖 න 𝑒 𝑡 𝑑𝑡 Donde 𝐾𝑖 es la ganancia del control integral. En cualquier tipo de controlador, la acción proporcional es la más importante, por lo que la constante 𝐾𝑃 𝐾𝑖 = 𝑇𝑖 Donde 𝑇𝑖 es un factor de proporcionalidad ajustable que indica el tiempo de integración. El equivalente en el dominio 𝑠 de la ecuación es: 𝑉 𝑠 = 𝐾𝑖 𝐸(𝑠) 𝑠 ∴ 𝐺𝑐 𝑠 = 𝑉(𝑠) 𝐸(𝑠) = 𝐾𝑖 𝑠 = 𝐾𝑃 𝑇𝑖 𝑠 Control integral I (Hernández, 2010) Control derivativo D (Hernández, 2010) Se dice que un control es de tipo derivativo cuando la salida del controlador v(t) es proporcional a la derivada del error e(t): 𝑑𝑒 (𝑡) 𝑣 𝑡 = 𝐾𝑑 𝑑𝑡 Donde 𝐾𝑑 es la ganancia de control derivativo. La constante 𝐾𝑑 puede escribir en términos de 𝐾𝑃 : 𝐾𝑑 = 𝐾𝑝 𝑇𝑑 Donde 𝑇𝑑 es un factor de proporcionalidad ajustable que indica el tiempo de derivación. El equivalente de la ecuación en el dominio 𝑠 es: 𝑉 𝑠 = 𝐾𝑑 𝑠𝐸(𝑠) ∴ 𝐺𝑐 𝑠 = 𝑉(𝑠) 𝐸(𝑠) = 𝐾𝑑 𝑠 = 𝐾𝑃 𝑇𝑑 𝑠 El significado de la derivada se relaciona con la velocidad de cambio de la variable dependiente, que en el caso del control derivativo indica que éste responde a la rapidez de cambio del error, lo que produce una corrección importante antes de que el error sea elevado. Control derivativo (Hernández, 2010) Además, la acción derivativa es anticipativa, esto es, la acción del controlador se adelanta frente a una tendencia de error (expresado en forma de derivada). Para que el control derivativo llegue a ser de utilidad debe actuar junto con otro tipo de acción de control, ya que, aislado, el control derivativo no responde a errores de estado estable. Control proporcional-integral: PI (Hernández, 2010) Se dice que un control es de tipo proporcional-integral cuando la salida del controlador v(t) es proporcional al error e(t), sumado a una cantidad proporcional a la integral del error e(t): 𝐾𝑃 න 𝑒 𝑡 𝑑𝑡 𝑣 𝑡 = 𝐾𝑃 𝑒 𝑡 + 𝑇𝑖 de manera que al expresar ecuación anterior en el dominio 𝑠, se tiene: 𝑉 𝑠 = 𝐾𝑃 𝐸 𝑠 + 𝐺𝑐 𝑠 = 𝑉(𝑠) 𝐾𝑃 𝐸(𝑠) 𝑇𝑖 𝑠 1 𝐾 𝑖 𝑖 𝐺𝑐 𝑠 = 𝐸(𝑠) = 𝐾𝑃 1 + 𝑇 𝑠 = 𝐾𝑃 + 𝑇 𝑃𝑠 𝑉(𝑠) 𝑠 + 1Τ𝑇𝑖 𝑠 + (𝐾𝑖 Τ𝐾𝑃 ) = 𝐾𝑃 = 𝐾𝑃 𝐸(𝑠) 𝑠 𝑠 La ecuación anterior, corresponde a un factor proporcional Kp que actúa junto con un cero ubicado en z = -1/Ti (cuya posición es ajustable sobre el eje real a la izquierda del origen) y un polo en el origen. Control proporcional-integral: PI (Hernández, 2010) Control proporcional-derivativo: PD (Hernández, 2010) Se dice que un control es de tipo proporcional-derivativo cuando la salida del controlador v(t) es proporcional al error e(t), sumado a una cantidad proporcional a la derivada del error e(t): 𝑑𝑒(𝑡) 𝑣 𝑡 = 𝐾𝑃 𝑒 𝑡 + 𝐾𝑃 𝑇𝑑 𝑑𝑡 Al expresar la ecuación anterior en el dominio 𝑠, se obtiene: 𝑉 𝑠 = 𝐾𝑃 𝐸 𝑠 + 𝐾𝑃 𝑇𝑑 𝑠𝐸 𝑠 ∴ 𝐺𝑐 𝑠 = 𝑉(𝑠) 𝐸(𝑠) = 𝐾𝑃 1 + 𝑇𝑑 𝑠 𝑉(𝑠) 𝐺𝑐 𝑠 = = 𝐾𝑃 𝑇𝑑 𝑠 + 1Τ𝑇𝑑 = 𝐾𝑃 𝑇𝑑 𝑠 + (𝐾𝑃 Τ𝐾𝑑 ) 𝐸(𝑠) La ecuación anterior, indica un factor proporcional Kp Td, que actúa junto con un cero z = -1/Td, cuya posición es ajustable en el eje real. Control proporcional-derivativo: PD (Hernández, 2010) Control proporcional-integral-derivativo: PID (Hernández, 2010) Se dice que un control es de tipo proporcional-integral-derivativo cuando la salida del controlador v(t) es proporcional al error e(t), sumado a una cantidad proporcional a la integral del error e(t) más una cantidad proporcional a la derivada del error e(t): 𝐾𝑃 𝑑𝑒(𝑡) 𝑣 𝑡 = 𝐾𝑃 𝑒 𝑡 + න 𝑒 𝑡 𝑑𝑡 + 𝐾𝑃 𝑇𝑑 𝑇𝑖 𝑑𝑡 Por lo que en el dominio de 𝑠 le corresponde la expresión: 𝐾𝑃 𝑉 𝑠 = 𝐾𝑃 𝐸 𝑠 + 𝐸 𝑠 + 𝐾𝑃 𝑇𝑑 𝑠𝐸(𝑠) 𝑇𝑖 𝑠 ∴ 𝐺𝐶 𝑠 = 𝐺𝐶 𝑠 = 𝐺𝐶 𝑠 = 𝑉(𝑠) 𝐸(𝑠) 𝑉(𝑠) = 𝐸(𝑠) 2 = 𝐾𝑃 1 + 𝐾𝑃 1 𝑇𝑖 𝑠 + 𝑇𝑑 𝑠 𝑠+1Τ𝑇𝑖 +𝑇𝑑 𝑠 𝑠 = 𝑉(𝑠) 𝑠 + 1Τ𝑇𝑑 𝑠 + 1Τ𝑇𝑖 𝑇𝑑 = 𝐾𝑃 𝑇𝑑 𝐸(𝑠) 𝑠 𝐾𝑖 𝐺𝐶 𝑠 = 𝐾𝑃 + + 𝐾𝑑 𝑠 𝑠 La ecuación (8.17) indica un factor proporcional KpTd que actúa junto con un par de ceros (distintos, repetidos o complejos, cuya posición es ajustable en el plano s) y un polo en el origen. Control proporcional-integral-derivativo: PID (Hernández, 2010) Características de los diferentes controladores (Hernández, 2010) Control proporcional • El tiempo de elevación experimenta una pequeña reducción. • El máximo pico de sobreimpulso se incrementa. • El amortiguamiento se reduce. • El tiempo de asentamiento cambia en pequeña proporción. • El error de estado estable disminuye con incrementos de ganancia. • El tipo de sistema permanece igual. Control proporcional-integral • El amortiguamiento se reduce. • El máximo pico de sobreimpulso se incrementa. • Decrece el tiempo de elevación. • Se mejoran los márgenes de ganancia y fase. • El tipo de sistema se incrementa en una unidad. • El error de estado estable mejora por el incremento del tipo de sistema. Características de los diferentes controladores (Hernández, 2010) Control proporcional-derivativo • El amortiguamiento se incrementa. • El máximo pico de sobreimpulso se reduce. • El tiempo de elevación experimenta pequeños cambios. • Se mejoran el margen de ganancia y el margen de fase. • El error de estado estable presenta pequeños cambios. • El tipo de sistema permanece igual. Control proporcional-integral-derivativo • Este tipo de controlador contiene las mejores características del control proporcional-derivativo y del control proporcional-integral. Referencias Bibliográficas Katsuhiko Ogata. (2010). Ingeniería de Control Moderna 5ª ed. Madrid (España): Pearson Education. Nise Norman S. (2015). Control System Engineering 7th edition. USA: Wiley. Hernández G. Ricardo. (2010). Introducción a los sistemas de control: Conceptos, aplicaciones y simulación con MATLAB. Naucalpan, Edo de Méx.: Peason Education de México. Gomariz Spartacus, et. al. (2001). Teoría de Control: Diseño Electrónico. Barcelona (España): Alfaomega. Pinto B. Enrique, et. al. (2010). Fundamento de Control con Matlab. España: Pearson Education.