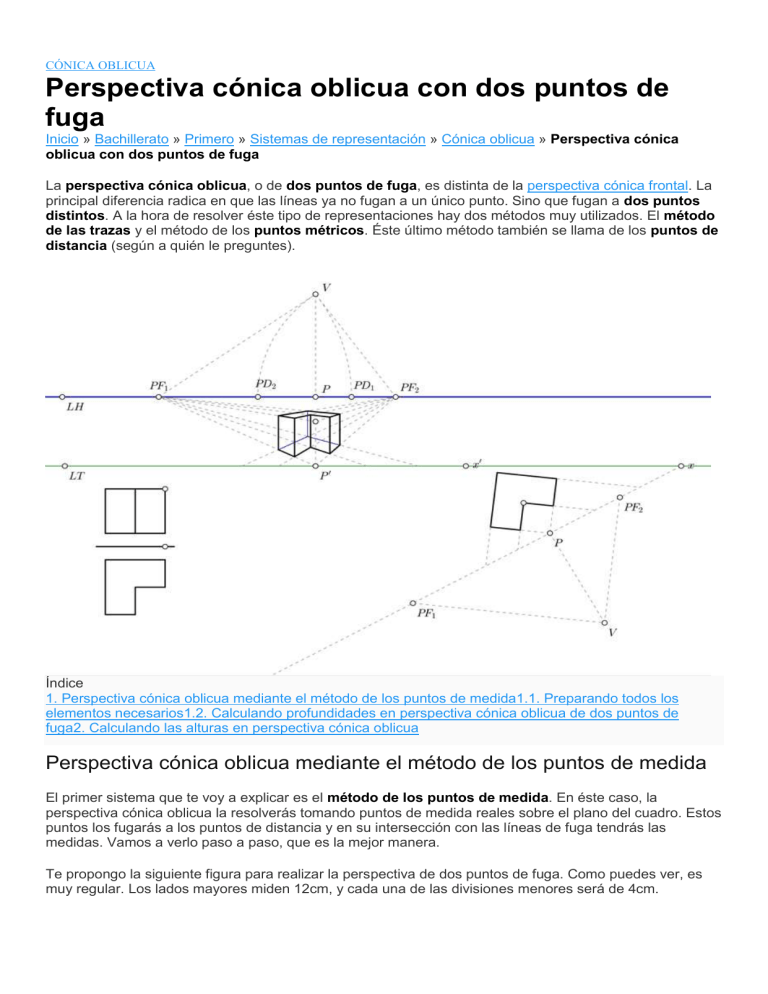
CÓNICA OBLICUA Perspectiva cónica oblicua con dos puntos de fuga Inicio » Bachillerato » Primero » Sistemas de representación » Cónica oblicua » Perspectiva cónica oblicua con dos puntos de fuga La perspectiva cónica oblicua, o de dos puntos de fuga, es distinta de la perspectiva cónica frontal. La principal diferencia radica en que las líneas ya no fugan a un único punto. Sino que fugan a dos puntos distintos. A la hora de resolver éste tipo de representaciones hay dos métodos muy utilizados. El método de las trazas y el método de los puntos métricos. Éste último método también se llama de los puntos de distancia (según a quién le preguntes). Índice 1. Perspectiva cónica oblicua mediante el método de los puntos de medida1.1. Preparando todos los elementos necesarios1.2. Calculando profundidades en perspectiva cónica oblicua de dos puntos de fuga2. Calculando las alturas en perspectiva cónica oblicua Perspectiva cónica oblicua mediante el método de los puntos de medida El primer sistema que te voy a explicar es el método de los puntos de medida. En éste caso, la perspectiva cónica oblicua la resolverás tomando puntos de medida reales sobre el plano del cuadro. Estos puntos los fugarás a los puntos de distancia y en su intersección con las líneas de fuga tendrás las medidas. Vamos a verlo paso a paso, que es la mejor manera. Te propongo la siguiente figura para realizar la perspectiva de dos puntos de fuga. Como puedes ver, es muy regular. Los lados mayores miden 12cm, y cada una de las divisiones menores será de 4cm. La altura del observador es de 10cm y se encuentra separado del plano del cuadro 15cm. Como puedes ver, la inclinación del plano del cuadro respecto a la figura es de 30 grados. Todas éstas medidas están pensadas para trabajar en formato A3 en formato apaisado. Si vas a trabajar en un A4, tienes que dividir todas las medidas a la mitad. Preparando todos los elementos necesarios Vamos a empezar por el principio. En cualquier ejercicio de perspectiva cónica oblicua lo primero que tenemos que dibujar son la línea de tierra y la línea del horizonte. Para hallar los puntos de fuga y distancia, yo recomiendo trabajar hacia abajo. De esa manera podrás dibujar también en la misma hoja la planta de la figura. Ten en cuenta que no necesitas dibujar todas esas líneas. Solo necesitas marcar los puntos. Eso significa que una vez los tengas puedes borrar todos los pasos intermedios y así tendrás más espacio en la hoja. Antes de nada, piensa que tamaño tiene la figura. En éste caso mide 12cm de alta, por lo que algún punto estará por encima de la línea del horizonte. Sabiendo ésto, marca la línea del horizonte al menos 3cm por debajo del borde de la hoja. Así dejarás 1cm de margen. A la misma distancia que la altura del observador (en este caso 10cm), traza una paralela, que se será la línea de tierra. Marca el punto de vista del observador P sobre la línea del horizonte. Si el ángulo de la figura con el plano del cuadro es 45 grados, ponlo centrado, si es de 30, más cerca del lado izquierdo. Como a 1/3 del total de la hoja del borde. Si es de 60, ponlo más cerca del lado derecho, como a 2/3 del borde izquierdo. Desde el punto P traza una perpendicular la línea de tierra y mide la distancia que separa al observador del plano del cuadro. En éste ejercicio es de 15cm. Así obtienes el punto V. Usando escuadra y cartabón, haz el ángulo que te corresponda (en este ejercicio 30 grados hacia la derecha y 60 hacia la izquierda) para hallar los puntos de fuga. Para no liar, llámalos PFd y PFi (Punto de fuga derecha y punto de fuga izquierda). Pincha en PFd y con el compás mide hasta V, si no te abre suficiente el compás, puedes usar un alargador. ¿Que no tienes alargador? Atento a la siguiente imagen. Es un truco para profesionales. Con centro en PFd y un radio cualquiera traza un arco que corta en E y F. Haz una paralela al segmento EF que pasa por V. Ya tienes el punto de distancia. Al punto de distancia te recomiendo llamarlo PDd aunque esté al lado izquierdo. Más que nada porque a éste punto fugarás todas las medidas que hagan referencia al PFd Desde PFi traza un arco con radio hasta V. Donde corta a la LH ya tienes el PDi Donde el segmento que une P con V corta a la LT, marca el punto P’. Ya lo tenemos todo preparado. Es hora de empezar a dibujar. Calculando profundidades en perspectiva cónica oblicua de dos puntos de fuga Lo primero que debes entender es que no puedes calcular profundidades de cualquier punto. Tan solo puedes calcular distancias sobre las líneas que fugan desde P’ hasta PFd y PFi Sabiendo ésto, lo primero que debes hacer es dibujar las líneas que unen P’ con PFd y PFi. Sobre ellas vas a calcular las medidas en profundidad. A la línea que une P’ con PFd la llamaremos r, y a la que une P’ con PFi la llamaremos s. Para calcular las medidas en perspectiva cónica oblicua, debes tomarlas primero sobre el plano del cuadro. Así pues, mide las profundidades en medida real sobre el plano del cuadro, 4, 8, 12 a la derecha y otros tantos a la izquierda. Desde los puntos que has marcado a la izquierda, debes trazar líneas hacia el punto de distancia opuesto. Es decir PDi, que se encuentra a la derecha del punto P. Recuerda que el punto de distancia siempre estará opuesto al punto de fuga respecto al punto P. Estas trazas cortan a la recta s en los puntos 4′, 8′ y 12′. Esos puntos representan las distancias en profundidad sobre esa línea. Llegados a éste punto, es interesante recordar que en la perspectiva cónica oblicua de dos puntos de fuga, las líneas paralelas entre si no son paralelas en la representación. En éste caso, todas ellas fugan a los puntos de fuga PFd o PFi. Dibuja las rectas que unen 4′, 8′ y 12′ con PFd, todas ellas se encuentran a 4, 8 y 12cm de la recta r. Ahora dibuja las rectas que unen los puntos que miden 4, 8, y 12 al lado derecho del punto P’ sobre la línea de tierra, con el PDd, en la intersección con s tienes la representación en profundidad de esas medidas. Las llamaremos 4», 8» y 12». Traza las rectas que unen 4», 8» y 12» con PFi, todas esas rectas están a 4, 8 y 12cm de la recta s. Para hacer la visualización más fácil, borra todos los pasos intermedios, y quédate solo con las líneas que definen la planta. De ese modo podrás dibujar en perspectiva cónica oblicua de dos puntos de fuga mucho más fácilmente. Calculando las alturas en perspectiva cónica oblicua Ésta sea tal vez la parte más difícil de la perspectiva cónica oblicua. Al igual que pasaba con la perspectiva cónica frontal, solo puedes tomar medidas reales sobre el plano del cuadro. Como la única parte de la figura que está en contacto con el plano del cuadro es la arista que tiene su base en P’, las deberás tomar sobre su vertical. Otra alternativa sería tomarla sobre las trazas, lo que se conoce como el método de las trazas en perspectiva de dos puntos de fuga. Levanta una perpendicular a la línea de tierra que pasa por P’, y sobre ella mide 4, 8 y 12cm. Une estos puntos con PFd y PFi Para identificarlos, llama A al punto que mide 4cm, B al punto que mide 8cm y C al punto que mide los 12cm. Todos los puntos de esas líneas se encuentran a 4, 8 y 12cm sobre el suelo. Si unes P’ con el punto que marca los 8cm, ya tienes una línea de la figura. Puedes unir P’ con 12′ por un lado y con 12» por el otro. Esas también son dos líneas de la figura. A continuación, te voy a explicar como levantar algunas alturas más. Si te fijas bien, éste método para dibujar en perspectiva cónica oblicua se basa sobretodo en hallar intersecciones. Las más fáciles ahora son las que salen de unir perpendiculares a los puntos de la planta, con las líneas que definen las alturas. Traza una perpendicular por 4», al punto donde corta a la línea que va de C a PFd tienes el punto C4», que forma parte de la figura. Puedes trazar sin miedo la línea que une el punto que marca los 8cm de altura con el punto C4» Ahora dibuja una perpendicular a la línea de tierra que pasa por 12», en el punto donde corta a la línea que va de C a PFd tienes el punto C12», que también forma parte de la figura. Une C4» con C12», y C12» con 12». Esas dos líneas son dos aristas visibles de la figura. Dibuja la línea que une C4» con PFi Para continuar, llama D a la intersección de 4′ con 4». A la intersección de 8′ con 4» llámala E. Y a la intersección de 12′ con 4» llámala F. Levanta perpendiculares a la línea de tierra que pasen por D, E y F. A las intersecciones con la línea que va de C4» a PFi llámalas DC4′‘, EC4» y FC4». Puedes unir C4» con DC4» por un lado, y EC4» con FC4» por el otro. Esas también son dos aristas visibles de la figura. Los puntos F, E y D los puedes borrar, junto con las perpendiculares, ya no las vas a necesitar más. De esa manera también te liarás menos. Levanta perpendiculares a la línea de tierra que pasen por 4′, 8′ y 12′. A las intersecciones con la línea que va de B a PFi llámalas B4′, B8′ y B12′. Puedes unir B12′ con B8′ por un lado, y B4′ con B. Esas son dos aristas visibles de la figura. A la intersección de las perpendiculares que suben desde 4′ y 8′ con la recta que va de A hasta PFi llámalos A4′ y A8′ para identificarlos. Puedes unir A4′ con A8′. También A4′ con B4′ y para finalizar A8′ con B8′. Todas esas son también aristas visibles. Ya casi hemos terminado. Une B12′ con FC4». Luego une B8′ con EC4». Para terminar éste paso, une B4′ con DC4». Esas tres son aristas visibles de la figura. Haz una línea auxiliar que una A8′ con PFd y mira donde corta a la línea que une A4′ con B4′. Ese pequeño segmento es una parte vista de la arista. La última línea la obtienes de la intersección de la línea auxiliar que va de EC4» hasta PFi con la línea que une B4′ con DC4». Tal vez éstas dos últimas líneas te han dejado un poco fuera de lugar. Recuerda que todas las líneas que son paralelas entre si (en éste caso a la línea que une P’ con 12», fugan todas al mismo punto. Por eso sabes que las líneas que buscas están sobre esas líneas que acabas de marcar. …y éste es el resultado de tu obra.