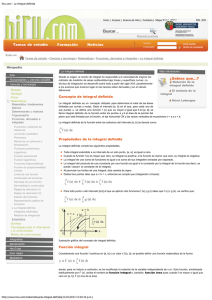
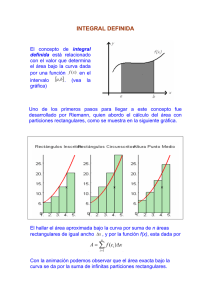
República Bolivariana de Venezuela Ministerio del Poder Popular para la Educación Universitaria UPTA “Federico Brito Figueroa” PNF de Telecomunicaciones Trayecto I, Intervalo III Matemática Integrante: Misael Campos Tutor: Marisabel León 29.943.221 La Victoria, 22 de marzo de 2023 Introducción . En el ámbito de las matemáticas, una de las ramas más interesantes y complejas es el cálculo integral. Este campo se enfoca en el estudio de funciones y sus propiedades, centrándose en la noción de cambio y acumulación. Dentro del cálculo integral, las integrales definidas son una de las herramientas más importantes y útiles. En este informe, se explicará en detalle qué son las integrales definidas, cómo se calculan y algunos de sus usos más comunes. Integral definida . Una integral definida es una herramienta matemática que se utiliza para medir el área bajo la curva de una función. En términos simples, la integral definida se puede entender como la suma de infinitos rectángulos que cubren el área bajo la curva de una función en un intervalo determinado. En otras palabras, una integral definida se utiliza para encontrar el área exacta entre la curva de una función y el eje x en un intervalo determinado. . La integral definida se representa de la siguiente manera: . Donde f(x) es la función que se está integrando, a y b son los límites de integración y dx representa una pequeña cantidad de cambio en x. En resumen, la integral definida es el resultado numérico que se obtiene al calcular el área bajo la curva de una función en un intervalo determinado. Cálculo de integrales definidas . El cálculo de integrales definidas puede ser un proceso complejo y laborioso, pero con las herramientas adecuadas y la práctica suficiente, puede ser realizado con relativa facilidad. Para calcular una integral definida, se deben seguir los siguientes pasos: • Identificar la función f(x) que se desea integrar. • Establecer los límites de integración a y b. • Aplicar la regla de integración correspondiente para obtener la antiderivada de la función f(x) (también conocida como primitiva). • Evaluar la antiderivada en los límites de integración a y b. • Restar el valor obtenido en el paso 4 para encontrar el valor de la integral definida. . Es importante tener en cuenta que el valor de la integral definida puede ser positivo, negativo o cero, dependiendo de la forma de la función y los límites de integración establecidos. Usos de las integrales definidas . Las integrales definidas tienen una amplia variedad de aplicaciones en muchas áreas diferentes. A continuación, se presentan algunos de los usos más comunes de las integrales definidas: • Cálculo de áreas y volúmenes: como se mencionó anteriormente, las integrales definidas se utilizan principalmente para calcular el área bajo la curva de una función en un intervalo determinado. También se pueden utilizar para calcular el volumen de sólidos de revolución. • Modelado de fenómenos físicos: las integrales definidas se utilizan para modelar fenómenos físicos y calcular cantidades como la velocidad, la aceleración y la cantidad de trabajo realizado. • Análisis de datos: las integrales definidas se utilizan para analizar datos y calcular estadísticas como la media, la mediana y la moda. • Cálculo de probabilidades: las integrales definidas se utilizan en la teoría de la probabilidad para calcular la probabilidad de eventos continuos. Teoremas para integrales definidas Teorema fundamental del cálculo . El teorema fundamental del cálculo es uno de los más importantes en el cálculo integral y establece una relación entre la derivación y la integración. Este teorema establece que si f(x) es una función continua en el intervalo [a, b], entonces la función F(x) definida como: es una antiderivada de f(x). En otras palabras, si f(x) es continua, entonces la integral definida de f(x) en un intervalo [a, b] puede ser calculada encontrando una antiderivada de f(x) y evaluándola en los límites de integración. . Este teorema es muy útil para simplificar la evaluación de integrales definidas, ya que permite calcular la antiderivada de la función f(x) y evaluarla en los límites de integración, en lugar de tener que calcular la integral directamente. Teorema del valor medio . El teorema del valor medio establece que si f(x) es una función continua en el intervalo [a, b], entonces existe un número c en el intervalo (a, b) tal que: . En otras palabras, el teorema del valor medio establece que hay al menos un punto c en el intervalo [a, b] donde el valor de la función f(x) es igual al valor promedio de la función sobre ese intervalo. . Este teorema es útil para entender el comportamiento promedio de una función en un intervalo determinado y se utiliza a menudo en análisis de datos y estadística. Teorema de cambio de variable . El teorema de cambio de variable establece que si u = g(x) es una función continua y diferenciable en el intervalo [a, b] y f(u) es una función continua en el intervalo [g(a), g(b)], entonces: . En otras palabras, este teorema establece que, si se realiza un cambio de variable en una integral definida, la integral resultante es igual a otra integral definida en términos de la nueva variable. . Este teorema es muy útil para simplificar el cálculo de integrales definidas complejas mediante la sustitución de una variable más simple. Teorema de integración por partes . El teorema de integración por partes establece que si u(x) y v(x) son dos funciones diferenciables en el intervalo [a, b], entonces: . En otras palabras, este teorema establece que, si se integra el producto de dos funciones, es posible descomponer la integral en dos términos y reducir la complejidad de la integral. . Este teorema es muy útil para simplificar el cálculo de integrales definidas de productos de funciones complicadas. Linealidad . La integral definida es una función lineal del integrando. Esto significa que si f(x) y g(x) son dos funciones continuas en el intervalo [a, b], y k es una constante, entonces: 𝑏 𝑏 𝑏 ∫ [𝑘𝑓(𝑥) + 𝑔(𝑥)]𝑑𝑥 = 𝑘 ∫ 𝑓(𝑥)𝑑𝑥 + ∫ 𝑔(𝑥)𝑑𝑥 𝑎 𝑎 𝑎 . En otras palabras, la integral de una suma de funciones es igual a la suma de las integrales de cada función individual. Simetría . Si f(x) es una función simétrica alrededor del punto c, entonces: 𝑐 𝑐+𝑎 ∫ 𝑓(𝑥)𝑑𝑥 = ∫ 𝑐−𝑎 𝑓(𝑥)𝑑𝑥 𝑐 . En otras palabras, la integral desde c-a hasta c es igual a la integral desde c hasta c+a. Aditividad . Si f(x) es una función continua en el intervalo [a, b], y c es un punto en el intervalo (a, b), entonces: 𝑏 𝑐 𝑏 ∫ 𝑓(𝑥)𝑑𝑥 = ∫ 𝑓(𝑥)𝑑𝑥 + ∫ 𝑓(𝑥)𝑑𝑥 𝑎 𝑎 𝑐 . En otras palabras, la integral desde a hasta b es igual a la suma de las integrales desde a hasta c y desde c hasta b. Cambio de variable . El cambio de variable es una propiedad importante de las integrales definidas que permite simplificar la evaluación de integrales. Si u = g(x) es una función continua y diferenciable en el intervalo [a, b] y f(u) es una función continua en el intervalo [g(a), g(b)], entonces: 𝑏 𝑔(𝑏) ∫ 𝑓(𝑔(𝑥))𝑔′ (𝑥)𝑑𝑥 = ∫ 𝑎 𝑓(𝑢)𝑑𝑢 𝑔(𝑎) . En otras palabras, si se realiza un cambio de variable en una integral definida, la integral resultante es igual a otra integral definida en términos de la nueva variable. Valor absoluto . La integral del valor absoluto de una función es mayor o igual que el valor absoluto de la integral de la función. Es decir, si f(x) es una función continua en el intervalo [a, b], entonces: 𝑏 𝑏 |∫ 𝑓(𝑥)𝑑𝑥| ≤ ∫ |𝑓(𝑥)|𝑑𝑥 𝑎 𝑎 Valor medio . El teorema del valor medio establece que si f(x) es una función continua en el intervalo [a, b], entonces existe un número c en el intervalo (a, b) tal que: 𝑏 1 𝑓(𝑐) = ∫ 𝑓(𝑥)𝑑𝑥 𝑏−𝑎 𝑎 . En otras palabras, el teorema del valor medio establece que hay al menos un punto c en el intervalo [a, b] donde el valor de la función f(x) es igual al valor promedio de la función sobre ese intervalo. Monotonicidad . Si f(x) y g(x) son dos funciones continuas en el intervalo [a, b] y 𝑓(𝑥) ≤ 𝑔(𝑥) para todo x en el intervalo [a, b], entonces: 𝑏 𝑏 ∫ 𝑓(𝑥)𝑑𝑥 ≤ ∫ 𝑔(𝑥)𝑑𝑥 𝑎 𝑎 . En otras palabras, si una función es siempre menor o igual que otra función en un intervalo, entonces la integral de la primera función es menor o igual a la integral de la segunda función. Integración por partes . El teorema de integración por partes establece que si u(x) y v(x) son dos funciones diferenciables en el intervalo [a, b], entonces: 𝑏 𝑏 ∫ 𝑢(𝑥)𝑣 ′ (𝑥)𝑑𝑥 = [𝑢(𝑥)𝑣(𝑥)]𝑏𝑎 − ∫ 𝑣(𝑥)𝑢′ (𝑥)𝑑𝑥 𝑎 𝑎 . En otras palabras, este teorema establece que, si se integra el producto de dos funciones, es posible descomponer la integral en dos términos y reducir la complejidad de la integral. Cambio de orden de integración . El cambio de orden de integración es una propiedad importante de las integrales dobles y triples. Si f(x,y) es una función continua en un rectángulo 𝑅 = [𝑎, 𝑏] × [𝑐, 𝑑], entonces: 𝑏 𝑑 𝑑 𝑏 ∬ 𝑓(𝑥, 𝑦)𝑑𝐴 = ∫ ∫ 𝑓(𝑥, 𝑦)𝑑𝑦𝑑𝑥 = ∫ ∫ 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 𝑅 𝑎 𝑐 𝑐 𝑎 . En otras palabras, se puede cambiar el orden de integración de una integral doble o triple sin cambiar el valor de la integral. Teorema del valor medio para integrales dobles . El teorema del valor medio para integrales dobles establece que si f(x,y) es una función continua en un rectángulo 𝑅 = [𝑎, 𝑏] × [𝑐, 𝑑], entonces existe un punto (𝑥_0, 𝑦_0) en R tal que: 𝑓(𝑥0 , 𝑦0 ) = 1 ∬ 𝑓(𝑥, 𝑦)𝑑𝐴 𝐴(𝑅) 𝑅 donde A(R) es el área del rectángulo R. . Esta propiedad es útil para encontrar el valor promedio de una función en un rectángulo. Ejemplos Ejemplo 1 𝜋 ∫ sin(𝑥) 𝑑𝑥 0 Ejemplo 2 1 ∫ 𝑥 2 𝑑𝑥 −1 Ejemplo 3 1 ∫ 𝑒 𝑥 𝑑𝑥 0 Ejemplo 4 4 ∫ √𝑥 𝑑𝑥 1 Ejemplo 5 𝜋 2 ∫ cos(𝑥) 𝑑𝑥 0 Ejemplo 6 2 ∫ 𝑥 3 𝑑𝑥 −2 Ejemplo 7 1 ∫ ln(𝑥) 𝑑𝑥 0 Ejemplo 8 3 ∫ 1 1 𝑑𝑥 𝑥 Ejemplo 9 1 ∫ 𝑥 2 (1 − 𝑥 3 )𝑑𝑥 0 Ejemplo 10 Área entre una gráfica y el eje X . Si la función f no es no negativa en el intervalo [a,b], entonces su integral definida es el área que encerrada entre su gráfica y el eje OX: La representación corresponde a la gráfica de la función 𝑓(𝑥) = x 2 . El área que encierra su gráfica con el eje X en el intervalo [0,2] es la siguiente integral definida: Conclusión . Las integrales definidas son una herramienta matemática esencial en el cálculo integral. Se utilizan para medir el área bajo la curva de una función en un intervalo determinado y tienen una amplia variedad de aplicaciones en muchas áreas diferentes. Aunque el cálculo de integrales definidas puede ser un proceso complejo, con la práctica suficiente, se pueden calcular con relativa facilidad. En definitiva, las integrales definidas son una herramienta fundamental en las matemáticas y una de las bases del cálculo integral.