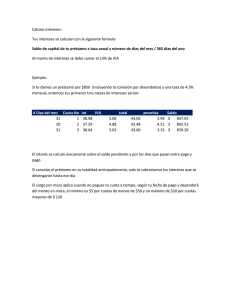
GUIA NO. 8 MATEMÁTICA FINANCIERA Y VALOR RAZONABLE DANIEL TINJACÁ RONCANCIO 1002 20/09/2023 3.1 a. Si tuviera dinero extra, pensaría en prestarlo, pero tendría que ver si es seguro y cuánto me pagarían extra por hacerlo. b. Si necesitara dinero, podría ir al banco o preguntar a amigos o familiares. Cuánto estaría dispuesto a pagar dependería de lo urgente que sea. c. Si mi amigo me presta $50,000 y me pide $5,000 extra en una semana, pensaré si realmente lo necesito y si puedo devolverlo a tiempo. d. Si es urgente y no tengo otra opción, podría aceptar el préstamo. e. Si yo prestara dinero, cobraría algo extra porque es un riesgo. Cobraría una cantidad justa comparada con otras opciones. f. El monto extra dependería de la tasa de interés y el riesgo. Lo calcularía para que sea justo y competitivo. 3.2 Aspecto Préstamo Bancario Financiamiento de la Universidad Documentación Mucha documentación Menos documentación enfocada en estudios y admisión Tasas de interés 6% - 8% anual 4% - 6% anual Periodos de pago Generalmente de 5 a 15 años Relacionado con la duración de la carrera Cuotas Mensuales Pueden ser fijas o variables según la universidad Beneficios Asesoramiento financiero, posibles ventajas fiscales Becas, facilidades para estudiantes, convenios para prácticas Costos ocultos Posibles comisiones y costos extras Algunos costos adicionales, generalmente más transparentes Creo que la opción de financiamiento de la universidad suena mejor. Aunque el banco puede tener tasas de interés un poco más altas, la universidad podría ofrecerme becas y otras ventajas para estudiantes. Pero, en realidad, dependería de las reglas de cada universidad y de mi situación financiera en ese momento. 3.3 3.3.1 - Interés: El interés es el costo que se paga por el uso del dinero prestado o la ganancia que se obtiene por invertir dinero en una entidad financiera. Cuando alguien toma un préstamo, debe pagar intereses adicionales al monto prestado, y cuando alguien ahorra o invierte dinero en un banco, recibe intereses como ganancia. - Tasa de interés: La tasa de interés puede ser definida por diversas entidades, incluyendo bancos centrales y entidades financieras. En una economía, el banco central, como la Reserva Federal en Estados Unidos o el Banco Central Europeo en la zona euro, juega un papel importante en la fijación de tasas de interés clave. Las tasas de interés pueden variar según la política económica, la oferta y la demanda de dinero, y otros factores macroeconómicos. - Matemáticas financieras y su importancia: Las matemáticas financieras, se centran en el estudio de conceptos relacionados con el dinero, inversiones, crédito y gestión financiera. Su importancia radica en su utilidad práctica para tomar decisiones financieras informadas y eficientes, tanto a nivel personal como empresarial. Estas herramientas matemáticas permiten calcular tasas de interés, valor presente, evaluar proyectos, determinar el valor de inversiones y planificar el ahorro para metas específicas, brindando la capacidad de gestionar y optimizar los recursos financieros en diversas situaciones. 3.3.2 Concepto Definición Fórmula Ejemplo Interpretación del Resultado Interés Simple El interés calculado solo sobre el capital inicial Interés = Principal x Tasa de interés x Tiempo $1,000 a 5% durante 3 años Al final de 3 años, ganarías $150 en interés simple. Interés Compuesto El interés calculado sobre el capital inicial y los intereses acumulados previos Fórmula de interés compuesto $1,000 a 5% durante 3 años Al final de 3 años, ganarías $157.63 en interés compuesto. Tasa Nominal La tasa de interés declarada antes de tomar en cuenta la frecuencia de capitalización Tasa Nominal = (Interés / Principal) x (n / t) 8% nominal anual, trimestralme nte capitalizado La tasa nominal es 8%, pero se capitaliza trimestralmente. Tasa Efectiva La tasa de interés real después de considerar la frecuencia de capitalización Tasa Efectiva = (1 + (Tasa nominal / n))^n - 1 8% nominal anual, trimestralme nte capitalizado La tasa efectiva es aproximadamente 8.24%. Tasa Periódica La tasa de interés aplicada en cada período de capitalización Tasa Periódica = (Tasa nominal / n) 8% nominal anual, trimestralme nte capitalizado La tasa periódica es 2% ya que se capitaliza trimestralmente. Tasa Vencida La tasa de interés aplicada al final del período 8% nominal anual con tasa vencida Los intereses se aplican al final del período. Tasa Anticipada La tasa de interés aplicada al principio del período 8% nominal anual con tasa anticipada Los intereses se aplican al principio del período. Tasa de Amortizació n La tasa a la que se paga un préstamo en cuotas periódicas 5% de amortización mensual Cada mes se paga el 5% del saldo restante del préstamo. Valor Presente El valor actual de una suma de dinero futura, descontada a una tasa de interés dada Fórmula de valor presente $1,000 en 3 años con tasa de interés del 6% El valor presente sería aproximadamente $839.62. Valor Futuro El valor de una suma de dinero en el futuro, después de ganar intereses Fórmula de valor futuro $1,000 a 6% durante 3 años El valor futuro sería aproximadamente $1,191.02. Anualidades Flujos de efectivo periódicos y constantes durante un período de tiempo Fórmula de anualidades Un depósito de $500 cada mes durante 2 años El valor de la anualidad sería $12,000. 3.3.4 Una tabla de amortización es una herramienta financiera que muestra el desglose de los pagos periódicos de un préstamo, incluyendo la cantidad aplicada al capital y la cantidad pagada en concepto de intereses en cada período. Aquí te muestro la estructura de una tabla de amortización simplificada y te explico cómo se calculan los componentes básicos utilizando un ejemplo: Supongamos que tomamos un préstamo de $20,000,000 a una tasa de interés del 10% anual a ser pagado en 12 meses. Período Saldo Inicial 1 Cuota Mensual Pago de Intereses Aporte a Capital Saldo Restante $20,000,000 $1,904,751 $166,667 $1,738,084 $18,261,916 2 $18,261,916 $1,904,751 $152,182 $1,752,569 $16,509,347 3 $16,509,347 $1,904,751 $137,445 $1,767,306 $14,742,041 4 $14,742,041 $1,904,751 $122,651 $1,782,100 $12,959,941 5 $12,959,941 $1,904,751 $107,799 $1,796,952 $11,163,989 6 $11,163,989 $1,904,751 $92,886 $1,811,865 $9,352,124 7 $9,352,124 $1,904,751 $77,910 $1,826,841 $7,525,283 8 $7,525,283 $1,904,751 $62,865 $1,841,887 $5,683,396 9 $5,683,396 $1,904,751 $47,747 $1,856,004 $3,827,392 10 $3,827,392 $1,904,751 $32,550 $1,872,201 $1,955,191 11 $1,955,191 $1,904,751 $17,264 $1,887,487 $67,704 12 $67,704 $1,904,751 $562 $1,904,189 $0 Saldo Inicial: En el primer período, el saldo inicial es el monto del préstamo, que es de $20,000,000. Cuota Mensual: La cuota mensual es de $1,904,751 y se mantiene constante durante los 12 meses. Pago de Intereses: El pago de intereses se calcula multiplicando el saldo inicial por la tasa de interés periódica. En el primer período, el pago de intereses es de $166,667. Aporte a Capital: El aporte a capital es la parte de la cuota que se utiliza para reducir el saldo del préstamo. Se calcula restando el pago de intereses de la cuota mensual. En el primer período, el aporte a capital es de $1,738,084. Saldo Restante: El saldo restante es el saldo inicial menos el aporte a capital. En el primer período, el saldo restante es de $18,261,916. 3.3.5 Ejemplo: Proyecto de Inversión en una Empresa Supongamos que tienes la oportunidad de invertir en un proyecto empresarial. Para este proyecto, debes realizar una inversión inicial de $50,000. A lo largo de cinco años, esperas recibir ingresos netos de efectivo de la siguiente manera: - Año 1: $10,000 - Año 2: $15,000 - Año 3: $20,000 - Año 4: $18,000 - Año 5: $25,000 Cálculo de la TIR: La TIR es la tasa de rendimiento que hace que el VPN sea igual a cero. Para calcular la TIR, buscamos la tasa que "iguala" la inversión con los ingresos futuros descontados al valor presente. En este caso, la TIR es aproximadamente del 15.78%. Esto significa que, dada la inversión inicial de $50,000 y los flujos de efectivo esperados, la tasa de rendimiento anual sería del 15.78% para que el proyecto sea rentable. Cálculo del VPN: El VPN es el valor presente de los flujos de efectivo futuros descontados a la tasa de descuento. Calculamos el VPN como la suma de los flujos de efectivo descontados en el tiempo presente: VPN = $10,000/(1 + 0.08)^1 + $15,000/1 + 0.08)^2 + $20,000/(1 + 0.08)^3 + $18,000/(1 + 0.08)^4 + $25,000/(1 + 0.08)^5 - $50,000 VPN ≈ $1,740.43 El VPN es positivo ($1,740.43), lo que significa que el proyecto generaría un valor adicional de $1,740.43 sobre la inversión inicial de $50,000. El proyecto generaría un retorno positivo sobre la inversión y, por lo tanto, se considera una buena oportunidad de inversión.