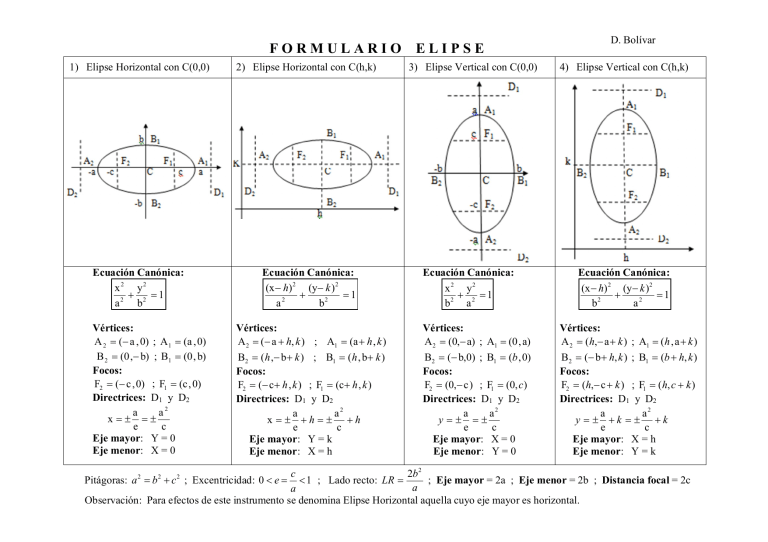
FORMULARIO 1) Elipse Horizontal con C(0,0) 2) Elipse Horizontal con C(h,k) Ecuación Canónica: x 2 y2 1 a 2 b2 Ecuación Canónica: (x h) 2 (y k ) 2 1 a2 b2 Vértices: A 2 ( a , 0) ; A 1 (a , 0) B 2 (0 , b) ; B1 (0 , b) Focos: F2 ( c , 0) ; F1 (c , 0) Directrices: D1 y D2 a a2 x e c Eje mayor: Y = 0 Eje menor: X = 0 Vértices: A 2 ( a h, k ) ; A1 (a h , k ) B2 ( h , b k ) ; B1 ( h , b k ) Focos: F2 ( c h , k ) ; F1 (c h , k ) Directrices: D1 y D2 a a2 x h h e c Eje mayor: Y = k Eje menor: X = h ELIPSE 3) Elipse Vertical con C(0,0) Ecuación Canónica: x 2 y2 1 b2 a 2 Vértices: A 2 (0, a) ; A1 (0, a) B2 ( b,0) ; B1 (b , 0) Focos: F2 (0, c ) ; F1 (0, c) Directrices: D1 y D2 a a2 y e c Eje mayor: X = 0 Eje menor: Y = 0 D. Bolívar 4) Elipse Vertical con C(h,k) Ecuación Canónica: (x h) 2 (y k )2 1 b2 a2 Vértices: A 2 ( h, a k ) ; A1 (h ,a k ) B2 ( b h, k ) ; B1 (b h, k ) Focos: F2 (h, c k ) ; F1 ( h, c k ) Directrices: D1 y D2 a a2 y k k e c Eje mayor: X = h Eje menor: Y = k c 2b 2 1 ; Lado recto: LR ; Eje mayor = 2a ; Eje menor = 2b ; Distancia focal = 2c a a Observación: Para efectos de este instrumento se denomina Elipse Horizontal aquella cuyo eje mayor es horizontal. Pitágoras: a 2 b 2 c 2 ; Excentricidad: 0 e









