Document
Anuncio

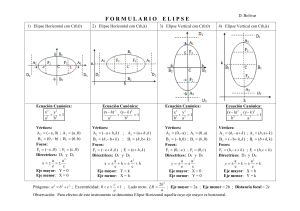
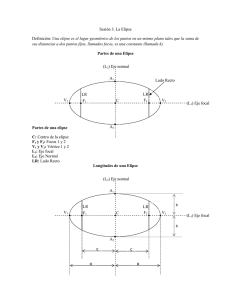
Durante muchos siglos se consideró que las órbitas de los planetas eran circunferenciales, con la Tierra como centro. Pero estudiando las observaciones hechas por Tycho Brahe sobre el movimiento del planeta Marte, Kepler descubrió en 1610, que los planetas giran alrededor del Sol de modo que sus trayectorias son elípticas y el sol ocupa uno de los focos La elipse es el lugar geométrico de todos los puntos P(x,y) cuya ubicación en el plano es tal que , la suma de sus distancias a dos puntos fijos de él es constante. Estos dos puntos fijos del plano, se llaman FOCOS y se designan por F1 y F2 B1 V2 F1 c b a b B2 c F2 a V1 FOCOS: Son los puntos fijos F1 y F2 CENTRO: Punto de intersección de las rectas focal y secundaria y que equidista de los focos . F1 F2 VÉRTICES : Puntos de intersección de la elipse con la recta focal. Se designan: V1 y V2 EJE MAYOR: Segmento que se considera de longitud 2a: “a” es el valor del semieje mayor . EJE MENOR: Segmento de la recta secundaria interceptada por la elipse . Se considera de longitud 2b “b” es el valor del semieje menor. Eje Menor = 2b Eje Menor V2 F1 B1 Eje Mayor = 2a Eje Mayor B2 F2 V1 2b 2 Lado Re cto = a y B ( b,0 ) V1 ( −a,0 ) F1 ( −c,0 ) P(x,y) F2 ( c, 0 ) V1 ( a, 0 ) x B ( −b,0 ) Consideremos la definición: d(P, F1 ) + d(P, F2 ) = cte = 2a y Eje mayor en el eje x x 2 2 x y + 2 =1 2 a b 2 y 2 x y + 2 =1 2 b a Eje mayor en el eje y x Determinar la ecuación de la elipse con focos (0,6) y (0,-6) y semieje menor 8 Determine la ecuación de la elipse cuyo eje menor es igual a 6 y su distancia focal es igual a 8. Determina los elementos de la elipse y grafícala, siendo su ecuación: 2 2 x y + =1 9 4 Sea el centro de la elipse el punto C(h,k) y el eje focal paralelo al eje x, luego: y k F2 centro ( h, k ) F1 (x − h)2 ( y − k)2 + 2 =1 2 a b x h Al desarrollar los cuadrados de binomio, ordenando la ecuación principal de la elipse e igualando a cero, encontramos la ecuación equivalente , llamada ECUACIÓN GENERAL DE LA ELIPSE Ax + By + Cx + Dy + F = 0 2 2 Graficar la Elipse que tiene por ecuación 25 x + 16 y + 100 x − 96 y − 156 = 0 . 2 2 Indique todos sus elementos. Hallar la ecuación general de la Elipse cuye eje mayor mide 20 unidades y los focos son los puntos de coordenadas ( 0,5 3 ) y ( 0, −5 3 )