A Reproduced
Copy
OF
Reproduced
for NASA
by the
NASA
FFNo 672 Aug 65
Scientific
and
Technical
Information
Facility
"l
r
I
DESCRIPTION
By
.:
. .Lu
OF
STRESS-STRAIN
Walter
Ramberg
CURVES
and
William
BY
THREE
R,
PARAMETERS
0sgood
i
SUMMARY
A simple
formula
is suggested
for describing
the
stress-strain
curve
in terms
of three
parameters:
namely,
Young_s
modulus
and
two secant
yield
strengths.
Dimensionless charts
are derived
from
this
formula
for determining
the stress-strain
curve,
the tangent
modulus,
and the
reduced
modulus
of a material
for.which
these
three
parameters
are given.
Comoarison
with
the tensile
and compressive data
on aluminum-alloy,
stainless-steel,
and carbonsteel
sheet
in NACA
Technical
Note
No. 840
indicates
that
the formula
is adequate
for most
of these
materials.
The
formula
does
not describe
the behavior
of alclad
sheet,
which
shows
a marked
change
in slope
at low
stress.
It
seems
probable
that
more
than
three
parameters
will
be
necessary
to represent
such stress-strain,
curves
adequately.
INTRODUCTION
,_ _ ....
: ....
. .:= _
,q..
An assembly
of the tensile
and compressive
stressstrain
.curves
for sheet
materials
characteristic
of aircraft
construction
is being
obtained
at the National
Bureau
of Standards
as the principal
objective
of a research
project
for the National
Advisory
Committee
for
Aeronautics.
Stress-strain,
stress-devlation,
secantmodulus,
tangent-madulus,
and reduced-modulus
curves
have
° been presented
in reference
1. for various
grades
of sheet
materials
of aluminum
alloy,
carbon
steel,
and chromiumnickel
steel.
A second
objecti_e
of the
same research
project
is a search
for yield
parameter,a
that
give
a better
description
of the
stress-strain
curve
than
those
in use
at present.
The conventional
descripti-on
of
the s.tress-strain
curve
of metals
by the
two parameters,
Young_s
modulus
and
yield
strength,
iS .inadequate
for
the efficient
design
of
members
unless
the material
follows
Hooke's
law up to. a
2
"_/•
NACA
Technical
Note
No.
902
/.k
-
yiel_
point
at which
it yields
indefinitely
under
constant
stress.
This
special
behavior
is approached,
for
example,
by certain
steels
(fig.
l) and
by
certain
low-strength
magnesium
alloys,
but
it
is not
characteristic
of many
high-strength
alloys
for
aircraft.
p._
r
alloy
_
Examination
sheet
and
of the
stress-strain
chromium-nickel-steel
curves
sheet
for
given
aluminumin ref-
erence
1 shows,
particularly
for
the
compressive
stressstrain
curves
(figs.
2 and
3),
a gradual
transition
from
the
elastic
straight
line
for
low
loads
toward
the
horizontal
line
characterizing
plastic
behavior.
The
type
of
transition
varies
widely.
Hence
there
is no
hope
of reducing
all
stress-strain
curves
to a single
typ_
of curve
by
uniform
stretching,
or affine
transformation
of coordinates.
This
rules
out
the
possibility,
which
exists
for
affinely
related
stress-strain
curves
(reference
2),
of complete
description
in terms
of only
two
parameters,
Youngts
modulus
and
secant
yield
strength.
A minimum
of three
parameters
will
be
required
to describe
the
changes
in shape
for
different
materials.
i _
Several
proposals
have
been
made
stress-strain
curve
in terms
of
three
Donnell
(reference
5)
suggests
as
two
the
stresses
s I,
s_,
strain
curve
is equal
Young_s
modulus.
The
at which
to 3/4
E
stress-strain
the
and
for
describing
the
or more
parameters°
yield
parameters
slope
1/4
curve
of
E,
is
the
stresswhere
_
is
then
derived
from
these
two
parameters
on
the
assumption
that
the
slope
varies
linearly
with
the
stress.
This
procedure
gives
a good
descriotion
of many
tensile
stress-strain
curves
of aluminum
alloys,
but
it does
not
seem
adequate
for
the
highly
curved
tangent-modulus
curves
found
for
the
compressive
stress-strain
properties
in reference
l,
from
which
figure
4 is
taken.
Furthermore
there
are
practical
sponding
quickly
difficulties
in determining
to
a tangent
modulus
of
8/4
from
the
stress-strain
curve.
Esser
stress-strain
and
Ahrend
curves
the
stresses
E
and
1/4
(reference
4)
noticed
for
many
materials
may
correE
that
the
be
approxi-
mated
by
two
straight
lines
when
they
are
clotted
• on loglog
paper.
They
orooosed
to
define
yield
strength
as
the
stress
at
the
intersection
of these
two
lines.
Description
of
strength
_ould
straight
line.
the
description
....
•
................................
the
stress-strain
curve
above
be
obtained
from
the
slope
of
The
proposal
is doubtless
an
by
an
offset
yield
strength.
.
•
.
.
................
the
yield
the
upper
advance
over
It has
the
NACA
..<
-
-
Technical
Note
No.
902
3
disadvantage,
however,
of requiring
the plotting
of sufficient
stress-strain
data
on log-log
paper
to determine
a straight
line
through
the points.
Furthermore
it gives
no informationabout
the shape
of the
important
transition
region
near
the intersection
of the two straight
lines.
c
• i_
¸.
,i
An analytical
expression
which
is suited
for theoretical
ling was proposed
by Nadai
in
expression
is
for the
stress-strain
studies
of plastic
1939
(reference
5).
-\
e = Ese
=
s'<
.....
S
ey-
>
Sp
s-
Sp
[
curve
buckThe
(i)
/
where
e
strain
s
stream
ey
strain
Sp
n
corresponding
proportional
to
yield
strength
Sy
limit
constan_
If the iogarithmof
both
sides
is
taken
in equation
(_),
it can be seen that
equation
(1) approaches
Esser
and
Ahrendls
two straight
lines
as asymptotes
for low and for
high
stress,
respectively.
The description
of the
transition region
is obtained
by increasing
the number
of parameters
from
three
to four.
k :i
In the
study
of plastic
bending,
the second
author
found
an analytical
expression
containing
three
parameters
that appeared
to be well
adapted
for representing
stressstrain
curves.
Further
examination
of the exoression
in
the light
of the data
given
in reference
1 confirmed
this
view.
I
4
NACA
Technical
ANALYTI
CAL
Note
EXPRE
Stress-Strain
No.
902
SSI ON
Curve
: • !ii
•ii
The
proposed
analytical
expression
E
where
becomes
K
and
the
n
same
is
(2)
•
are
constants.
as
equation
(2)
Sp=
Nadaits
if
expression
(1)
0
(3)
ey
that
the
is,
if
the
requirement
spond__ng
form
to
proportional
is
a
dropped
yield
The
expression
in terms
of
_
stress
the
=
K
limit
that
is
ey
taken
is
as
the
zero,
and
strain
corre-
dimensionless
(reference
6):
Sy.
(2)
may
be
follo_ving
written
variables
in
S I
(4)
S 1
J
,
•
r._
where
ordinate
of a
(fig.
Since
reduces
single
curve
sI
line
5),•
is the
secant
yield
strength,
equal
to
of the
intersection
with
the
stress-strain
through
the
origin
m I
being
a chosen
m I
is fixed,
all
affinely
curve.
The
abscissa
described
by
having
a
constant
slope
,
0
the
transformation
related
stress-strain
of the
intersection
equation
(2)
is
<
equal
ml <
(equation
curves
for
a
the
curve
to
i.
(_))
to a
stress-strain
m I
E
NACA Technical
ei
Note No. 90_
5
sl
-
+
mE
(5)
K
E
1
Inserting
equation
(4)
in
equation
Sl
From
equation
)n-I
gives
(6)
n
(5)
n-i
K
Inserting
(2)
V
equation
I ml
-
(7)
in
equation
i
= a +
(7)
mI
--
(6)
m I
gives
an
(8)
m I
f
Affinely
related
stress-strain
curves
that
by
equation
(8)
are
characterized
by having
of
n.
Figure
6 shows
a family
of
curves
different
values
of
n,
and
m I = 0.7.
Stress-Deviation
The
- ,. "-
stress-deviation
stress
against
elastic
strain
stress-strain
is
given
Curve
curve
difference
corresponding
curve
given
may
be described
the
same
value
for
a number
of
is
obtained
by
plotting
between
measured
strain
and
to
Hooke's
law.
For
the
by
equation
(2)
the
deviation
d
by
d
=
e-
s_ =
(9)
K(S
E
\ _,J
or
. -
.
",L
log
that
is,
a log-log
be a straight
line.
sionless
form
as
d
=
log
K
+
plot
of deviation
The
deviation
6 - Sd
S
1
nlog
s_
E
(I0)
against
stress
would
may
be written
in dimen-
(ll)
6
From
NACA
Technical
(9).,
(4),
equations
Note
90,2
No.
(8)
and
-
n
m1
or
1
1
log
8
=
-
m 1
log
+
nlog
G
(13)
m I
The
family
values
of
of
straight
n
and
lines
to
mI
=
corresoonding
0.7
Tangent
the
The
slope
that
from
tangent
of the
stress.
equation
modulus
tangent
is
to
shown
in
various
figure
7.
Modulus
at
to
a given
stress
the
stress-strain
The
reciprocal
(2):
of
the
is
tangent
defined
curve
modulus
as
at
is
! = __ = 1 + nK shn
E,
d.
{
{]
This
may
be
of
equations
written
(7)
and
in dimensionl'ess
(4):
E = 1 +
-
- m_ )
E I
ml
the
tangent-modulus
form
by
making
use
c n-l
(15)
k
Figure
8
against
shows
stress
ratio
Reduced
..,..
-
n(1
(.14)
•
_,
Modulus
ratio
with
for
mI
=
E'/E
plotted
0.7.
Rectangular
Section
.
•k
The
exceeds
(reference
ulus
columns
mated
E
reduction
the
by
the
in
proportional
7, pp.
159
a
reduced
actual
buckling
stress
limit
and
274)
is
by
modulus
E r.
buckling
stress
when
the
frequently
replacing
Thus
sr
stress
estimated
Young's
modin
the
would
case
be
of
esti-
_
as
sr
_
-
Er
-E
se
(16)
•
i_
_ _
NACA
wh,ere_
se
is
the
Technical
Note
buckling
stress
theory
and,
for
columns
from
reference
8,
of
Er
No.
comouted
rectangular
=
equation
(17)
_EE'
by
E
mr =
Figure
9
against
shows
the
stress
with
mI
=
(16)
Let
gives
4E '/E
a
may
(_e
(18)
for
ratio
different
be
=
solved
Er/E
values
Se
--;
for
(_r --
S1
that
(17")
plotted
of
n
and
0.7.
Equation
so
elasticL
section,
2
reduced-mo'dulus
ratio
from
crGss
(4_ + Jgr)
Dividing
902
equation
(16)
Er/E
as
follows:
(19)
Sr
Sl
becomes
Or
Er
(20)
(_e
Thus,
the
desired
intersection
of
reduced
(n)
in
1/(_ e
with
modulus
question.
may
the
DERIVATION
The
on log-log
materials
a straight
be
Er/E
EMPIRICAL
on
the
is
line
conveniently
point
adequacy
paper
given
line
of
straight
curve,
equation
Straight
lines
drawn
proper
OF
value
the
E
(18),
w.ith
by
ordinate
=
O/(_ e
for
the
FROM
curve
of
with
the
the
the
material
given
slope
connecting
circular
CONSTANTS
the
Er/E
the
in
STRESS-STRAIN
origin
figure
9.
CURVE
of
equation
(2)
was
tested
by plotting
the
stress-deviation
curves
for
the
sheet
in reference
1.
The
points
should
lie
on
according
to equation
(10)
if
equation
(2)
r
i
8
is
r
•
!
3
NACA
an
accurate
From
the
constants
Technical
Note
description
slope
and
K
and
Straight
stress-deviation
of
intercept
n
can
be
lines
were
curves
No
the
stress-strain
of
such
de_ermined
obtained
and
for
902
a
curve°
straight
for
a
line
the
best
fit.
for
all
the
compressive
all
but
four
of the
ten-
sile
curves
for
stresses
greater
tlian
the
stress
at which
the
secant
modulus
was
equal
to 90 percent
of Young's
modulus.
The
exceptions
had
stress-strain
curves
which
had
a gradual
change
of
slope
throughout
their
entire
length.
Thim
indicates
that
any
value
of
mI
0.90
would
give
an
approximate
fit
to compressive
Strain
curves
and
to most
tensile
stress-strain
at
stresses
It
such
mate
above
appeared
that
the
the
widely
that
corresponding
desirable
secant
used
offset.
In
other
appr o ximat
ely :
to
_'eld_
yield
choose
strength
strength
words,
sI
should
mI
=
the
value
than
stresscurves
0°90°
of
mI
sI
would
So. s
for
approxi0.2--oercent
be
to
chosen
satisfy
s
o.oo2 = e-
_!
i i_? _
; ....
to
less
(21)
E
[
where
(see
fig.
5)
e
S 1
-
(21a)
miE
inserting
1/m I
equation
(21a)
in
equation
(21)
and
solving
for
gives
r
1
--=
0.002
I
-
ml
Examination
ues
of
of
1
+
sl/E
tables
so.e/E
nickel
steels
1025
carbon
0.002
+
for
III
the
and
IV
aluminum
which
ranged
from
steel
in reference
of
its
relatively
value
was
low
_--
(21b)
So.alE
value
of
of
reference
alloys
1
and
1
the
gave
0.00258
to 0.00675;
was
not
included
this
ratio.
The
val-
chromiumthe
because
average
S
= 0.00486
(21c)
E
Substituting
for
mI ,
this
gives
average
_n
equation
(Ylb)
and
solving
"
.
• • "
,
L
•
.
NACA
Technical
No
Note
" 902
m I = 0.709
.. ..: .j:!
It
was
decided,
therefore,
to
(21d)
use
for
ml
the
value
m I = 0.7
for
determining
the
secant
(22)
yield
strength
s I.
W_nen
E
is known
and
sI
has been
determined,
it
is still
necessary
to know
the
shape
parameter
n
in
order
to establish
the
shape
of the
stress-strain
curve
according
to equations
(8) and
(4).
The
shape
parameter
n
is conveniently
the use
of a second
secant
yield
strength
sponding
to a second
secant
modulus
rosE,
In analogy
to equations
(5) and
(7),
e s -.
-
+
msE
derived
by
s2, correas follows.
(23)
K
E
•i
._-=
m 2
.
k
Solving
both
equations
(24)
z +z(,,.
(7)
and
(23)
for
K
gives
1
,; C<-,)
so
(25)
that
_i__
1
(26)
_h- l
m I
Solving
for
n
gives
m_
I-
mI
log
n =
1 +
mI
.......
log
1-m
s-kl
sm
s
(27)
l0
NACA
The
was
value
chosen
of
as
m s
Technical
for
the
second
=
ms
since
since
m =
tion
Note
up
most
Substituting
gives:
to
of
secant
(22)
(2)
=
1
is an
curves
(28)
=
+
in
1
relation
--
COMPARISON
_ITH
AND
The
describes
ues
to
of
13,
order
the
n
in
on
(29)
log
from
which
EXPERIMENTAL
to
data
ence
1.
The
approximation
practical
purposes.
In
were
obtained
from
the
puted
tion
s
A
from
between
equation
c
and
was
obtained
by
better
fit
would
been
determined
first
paragraph
procedure
used
cases.
than
S8
paper
is
STRESS-
TANGENT-MODULUS
3.08
the
-lO
log-log
of approximation
stress-strain
(27)
S 1
S 8
this
adequate
descripin reference
1.
equation
8 1
A plot
of
ure
10.
1.0
and
value
0.3853
+
log
strength
0.7
and
limiting
and
17
log-_
n
yield
(2,8)
between
of
the
which
equation
the
stress-strain
equations
902
0.85
this
value
lies
midway
it
is on the
safe
side
0.90
of
No.
given
in
fig-
STRAIN
CURVES
curve
w.ith which
equation
for
materials
with
c_
is brought
were
taken
at
out
in
random
(2)
val-
figures
ll
from
refer-
appears
to be
adequate
for
most
these
figures
E,
el,
and
ss
stress-strain
data,
and
n
was
com-
(27).
o,
Equation
and
the
multiplying
have
been
(8)
then
gave
relation
between
¢
by
obtained
sl/E
if
n
and
and
the
e
a
K
rela-.
and
by
had
s I.
from
a plot
of
the
data,
as
exolained
in
of the
preceding
section
(p.
7);
but
the
is simpler
and
probably
adequate
in most
A much
more
the
comparison
severe
with
test
the
of
the
adequacy
stress-strain
parison
with
the
tangent
modulus
- that
stress-strain
curve.
Such
a comparison
able
since
the
tangent
modulus
must
be
ing
the
reduced
modulus
in compression.
of
curve,
equation
is a
the
(2),
com-
is,
the
slope
of
the
seems
to be adviscomputed
for
evaluat(See
equation
(17).)
NACA
The
• i
tangent
Technical
moduli
in
Note
No.
compression
ll
902
of
reference
1
are
plotted
on a dimensionless
basis
in figures
14 to 21
together
with
computed
moduli
as given
by
figure
8.
The
value
of
n
from
equation
(29)
for
each
material
is given
in figures
14 to 21.
The
computed
moduli
are
shown
for
integral
values
of
n
and
for
n = 2.5.
To
appreciate
the
closeness
of fit,
therefore,
it
is necessary
to
interpolate
of
n
curves
values
between
the
curves
by using
the
particular
value
applying
to
the
plotted
data.
Except
for
the
with
a very
sharp
knee
(n
> 10)
the
experimental
of tangent
modulus
for
stresses
below
the
secant
yield
strength
sI
differ
less
than
_0.07
E
from
the
values
corresponding
to equation
(15).
In the
case
of the
values
with
the
sharp
knee
(fig.
21)
the
maximum
difference
was
considerably
greater.
These
differences
do not
detract
seriously
from
the
usefulness
of
equation
(2),
however,
since
the
region
in which
the
agreement
is not
good
comprises
a limited
this
range
the
difference
the
computed
values
of
of tangent
modulus
are
stress
range.
between
the
O
corresponding
small.
Consequently,
experimental
to a given
in
and
value
The
comparison
was
confined
to
the
materials
in reference
l, which
did
not
include
alclad
aluminum
alloys.
In the
alclad
aluminum
alloys
a change
in
slope
at
low
stress
is
observed
which
corresponds
to
the
yielding
of
the
aluminum
coating.
It
seems
probable
that
inclusion
of this
effect
will
require
the
addition
of at
least
one
more
parameter
EXAMPLE
to
FOR
the
three
APPLICATION
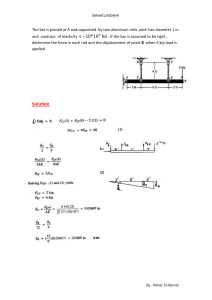
Computations
contained
0F
based
on
in
equation
THREE-PARAMETER
elastic
theory
(2).
METHOD
give
a
value
of
S
se
/
=
87
×
l0
pounds
for
the
critical
compressive
The
material
of the
specimen
strain
curve
shown
in
figuA'e
mine
the
stress:
per
inch
e
stress
of
a given
has
the
compressive
22.
It
is desired
specimen.
stressto deter-
Er
Sr
--
Se
E
which
account
is
an
estimate
of the
olastic
for
the
critical
stress
after
yielding
of
the
material.
taking
12
NACA
,
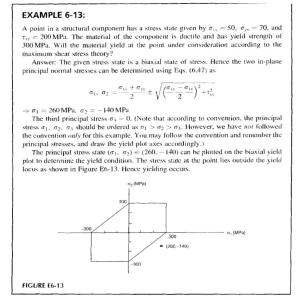
From
strengths
figure
Technical
22
are
Note
obtained
No.
the
902
two
secant
yield
|
so
s_
=
43.0
X 103
pounds
per
ss
= 38.0
x i03
poundsper
inch s
inch s
that
S1
-
I. 132
S_
From
figure
i0
this
corresponds
n=
Entering
ratio
figure
9 with
to
a
shaPe
parameter
8.15
this
value
of
n
and
with
th_
I
s_1
- _
se
43.0
87.0
_ 0.494
gives
_ 0.473
_E
E
so
that
the
corrected
critical
stress
3
sr
=
0.473
× 87
National
Bureau
Washington,
× lO
is
2
3"
=
41.2
of Standards,
D. C., April
X lO
8,
1943.
pounds
per
inch
NACA
Technical
Note
REFERENCE
i.
Aitchison,
C.
Pack
Alloy,
T.N.
2.
and
R. :
A
Jour.
13
902
S
Miller,
Compressive
Tests
of
1025
Carbon
Steel,
No.
840,
NACA,
1942.
0sgood,
W.
A.S.M.E.
pp.
S.,
No.
James
Some
and
A.:
Tensile
and
Sheets
of Aluminum
Chremium-Nickel
Steel.
Rational
Definition
App.
Mech.,
vol.
7,
of Yield
Strength.
no.
2, June
1940,
A61-A62.
•j
3.
Donnell,
L. H.:
tional
Limit
vol.
60,
no.
_.
Esser,
?
L
Suggested
and
Yield
ll,
Nov.
New
Definitions
for
ProporPoint.
Mech.
Engineering,
1938,
pp.
837-38.
•
Hans,
durch
werden.
eine
1939-40,
and
Ahrend,
H.:
Kann
die
ubereinkommenfreie
Arch.
f. Eisenhu_tenw.,
pp.
Grenze
13,
ersetzt
no.
10,
425-428.
5.
Holmquist,
J.
L.,
and
N_dai,
A.:
A Theoretical
and
Exoerimental
Approach
to
the
Problem
of Collapse
of •Deep-Well
Casing.
Paper
presented
at 20th
Annual
Meeting,
Am.
Petroleum
Inst.,
Chicago,
Nov.
1939.
6.
0sgood,
Nat.
pp.
W. R.:
Bur.
of
Column
Curves
and
Stress-Strain
Standards
Jour.
Res.,
vol.
9,
Diagrams.
Oct.
1932,
571-82.
7o
Timoshenko,
Hill
Book
S.:
Co.,
8.
von
Th.:
Karman,
Theory
Inc.,
of Elastic
New
York,
Untersuchungen
Stability.
N.
Y.,
1936.
uber
_._iitteilungen
uber
Forschungsarbeiten.
Ing.,
Heft
81,
1910.
r•
0.2%
Dehngrenze
vol.
McGraw-
Knickfestigkeit,
Ver.
deutsch.
NACA Technical
30
Note
No. 902
Figs.
(I bloc k °-10/50'1
8O
"]
.
7O
.
cb SO
c_-40
¢]
<O
09
q)
o) 3O
L.
¢3"
C
Ill
2O
0
_T
C
0
/0
•
09
C
0
L
0
.O0 /
.002
Sfroin
.003
.OOW
(D
II
8O
Figure
2.-
Sfr-ess-st-roin
blunt
knee,
our-ves
with
aluminum-alloy
CD
0
._Q
5O
24S-T,
thickness
0:064
incb._l__
_i_
y._-_-x
b"
%
%
_ 3O
<
/
o_"
ro
• 20
.
..
,
-.
/0
0
/
+
/
.001
o
X
•002
Troms
verse
fens/On
.... L omq/fud/mo/oompness/on-Tmclns verse
"
.003
.004 .OOE
S fr o/)o
.OOG
.007
--
.008
.008
1,2
NACA Technica
No-l-e No. 902
(:,sz/ot-_olq x)
\
%
%
J t < "' ¸
%
.,
.,
..
•
- ,
,
.,-
-.,
NACATechnical
ZOO
k
Note
!
No.
902
, .... .
Figs.
\
\:..- -Fconsverse coM,oress/on
\
\
• I
compress/on
i>!i_i
_
_.50
_
_1
0
.50
ZOO
/.
S/8 _td
Figure
4.-
thickness
Non-linear
variation
of tangent modulus with
stress; chromium-nickel
steel, full-hard,
0.020 inch.
56
/
/
iI
S=_e
l
/
!
J
I
I
40
l1///
_3z
_ee
I
16
/
I
//
,/.
o
.002
.004
.006
.008
S_rain
Figure
5.- Determination
of secant
yield strength.
4,5
NAC
. .-
F;q. 6
A Tli,chnlcal
, ,!#.
#
"'8
_)
__
+
_o
_D
II
O)
©
>
o
¢)
• ,-_ -_
U)
,7
_
|
II
,d
(D
%
0
°,-4
"<
\
X
\
I
L0 ,
_S'/S = p
\
NACA
Technical
Note
No.
Fig.
902
-.,
:J
•
r
/:
r
7
1
I!
7
I
_ACA
..
I
Technical
'io
No.90_
k
8
__
m
II --
M
Cb
l,n
--
II -
t
,
L
--- ----_------
I
/
._
--7
.....-.-
fJ
/
11
;/l//'/ ,////
"///,/,
4-3
o)
///// /¢//
;4
//A/ ,
II/,/ /
/
////
//,
i I-,.-I
or2
I=I
,-44-3...-..
• ,-4
/
/
.r.-I
["r _
/
block
-
10/32")
>
4-3
c_
(1
//2
c:)
0.
C
....
:
.............
."
.....................
I
NACA
.
•
_
................
I
Technical
ii
" !
"
:
":
/,,
i -i/
"
"
:-
NACA
•
Technical
Note
No.
Fig.
90_
I0
i
/5.0
10.5
,9.0
\
\
8.0
\
4.0
25
/.5
I
/.0
/./
,
It
I
P J
i
I
llqilll
/.2
I
F I
/.,3
I
I
I
I
I
t
I
t
I
I
[I
It
/.4
II
tllltl
ILllll_l
/.5
/.6
_,/e=
Figure
I0.-
Relation
between
log
n=l_-
zog
i?
-V
n
and
Sl/S 2 .
/IJllllll
/.7
JlllillJl
/-8
]LLIIIII
/.9
at.O
Note
I
No. 902
I
I
Figure
II.-
Figs.
I
I
I
I
Experimental
200
and
stress-strain
Cr-Ni
steel,
0.020
inch.
I
fUlll-hord,
1,12
I
computed
.,,_..,-,<'_"
curves_
--_----
thicknessl_J
_"
X../r"
/--11
l
Technical
_
NACA
l
/
¢'
'
_
/X.;
'
'
'
I
150
<
.
II
2_
0
0
_s
"/00
. 7S° .:"
.E
5O
d
002
O,
. !
Tension,
Longitudinal
Fr'c/n$ verse.
Compression,
Long/ltud/no/
Ff or?svef
s8.
dr'ed
A
+
$z
"
n__
26,/20
8Z3 5Z4 208
29. 660 205. 6/62. 7 zl.81
o
x
004
_
1000/b/s#7 in.
2#,770 18#. 7/473
4.83
29,010 1800/32.7
zl.58
puled
.006
Strain
.OO8
.012
.010
I00
MeosFension,
L ongi fudino/
7tons
verse.
Compression
L ongi fud/nol
Tr'onsver-se.
80
ured
a
+
Cor_puled
o
x
_b
<.
uf
I
E
s,
s,
tt
/000
Ib/sq in.
IO..EO0 52.2
5/.8 121.4
10,430
4_
,#ll.6
10.93
/06#.0
I0, 710
43.2
48.0
39./
45.6
9..88
13.43
..X._..._;-
_-'_-
-
_
_.
-
:d:o _c
2O
/
A Jc2
a I um Inum
- Experimental
stress-strain
alloy
24S-T,
ancl computed-curves;
thickness
0.064
i r_ch.
I
0
.002
I
0O4
I
•006
S#-oin
.008
. OI 0
.012
.
.... :.... _ .: ........ :_:::
NACA
........ :i :,¸
Technical
Nofe
i
No.
!_._/::
:::
:L :
..__:, : ......................................
902
Figs.
/00
8O
.c
o
o3
II
2_
_f
0
0
_Q
Measb_ r
Tensi-_,
ured
Transverse.
Compression
Longitudinal
Longitudinal
-_
Campuled
+
.......
_
o
Transverse.
E
I000
_
sz
Iblsq
in.
n
--
-
3/,620
64/
GS,/
oo
- ..
30,060
30,780
32,660
62S
b_.b
G3.4
$38
61.0
63.3
oo
oo
oo
x
i
I
i
0
•O01
002
.003
.004
Sfruin
Figure
t3.-
Experimenfol
corbon-sfeel,
end compufed
fhickness=O.054".
sTress-sfroin
curves,
1025
q
ZOO
rl
o 292
Mu
Cr=/V/"
sfeel
far
/e I
,
full-hard
/nch
fh.
0.020
Iomq.
.8O
.8O
B"
,n =2
.40
0
.20
.40
.80
.80
LO0
lQO
/,40
G=S/8_
Figure
14.- Experimenfal
2<n<3.
ond compufed
fongenf
moduliin
compression,
13,14
<
,.. '
,.• LI
I
L
NACA
Technical
Note
No. 902
Figs.
I
,.!•7
i:-¸ L::•_
::i!:
LO0
_
I
o 3.48
+ 3.83
_
3.10
_ 3.08
.80
Mo fer
OczNi
......
,,
X
_a'_
I
"
I
/o I
steel
I
I
1/4 hard
....
"
"
.......
....
I
Inch
fh.
/12
......
314
full
......
"
"
"
"
I/4
I
15,16
I
0020
long.
'_
.024
.020
-
"
"
trans.
_\
CD
OD
.60
I
-E-
0
0
.40
_Q
_0
o_
.20
X
_
o
o
t
0
0
.20
Figure
t5.-
.40
._0
Experimenfa]
compPessiom,
0498
A 410
1.00 ---_=
.80
/.00
d=S/S,
and
comoufed
3<n<4.
Cr-/vi
......
steel
t_._.ge
-,-,_
/.40
fomc)enf
moduli
ful/-hord
1/2
"
+,<.18......
x,<.si '; ....
.80
/.20
0.0275
.0 0
3i4 ....
,'_ll ;;
..........
in
long.
trs.
.o2.+
,.
\\
E'
,,,,,"
20
v
0
.20
Figure
16.-
.40
.80
.80
ExpePimenfal
and
compnessioP,,
4<n<5.
/.00
compufed
.....
5
/20
fongen¢
140
moduli
in
Technical
/.00
,.
. =*..
: L L :..,.
#
Note
No.
-
902
Figs.
17, 18
.80
;i
.60
LO
.
OJ
0
-...
II
0
0
_Q
in
compression
6<n<7
%
(
.20
n
o 6.72
0
Mc/fe/-iol
Or--N/Sfeel
full-ho/-d
.20
.40
fh.
._0
.80
Inch
0.02 75 tr-ons.
ZOO
120
d = sis,
.
.._
ZOO
.80
._0
E'
a
o
-E-
71
Mafer/'al
Z82 Al-ol/oy
24S-T
7.60
"
fh. 0.08/
"
.032
Inch
/on_7"
.40
I
.2O
Figure 18.-Experimental
and
co.mputed tangent modu
in
0
I
compresslon.
20
7<n<8.
dO
60
d=s/sl
..Irl
=7
.80
zOO
120
NACA
.
.-<.
,
Technical
Note
No. 902
Figs.
I 9,20
r:
.80
_
n
8.59
LO
Od
AAofer/'d/
E'
o
AI-olloy
7_-
+ 8.32 "
x 8.01
8.20
24S-RTth.
long.
II
0
0
._0
_Q
v
I
Figure
.2O
19-Experimenta
puted
tangent
compression.
_<_<9
0
.20
4O
end commoduli
n
.-_ =8
60
#=s/s,
.80
ZOO I
i
.80
6O
E'
-E-
o
Mafer/al
Inch
A/-o//oy/TS-T fh.0.032 long.
x 9.07 .....
24S- T ......
-9.88 ..........
084 " "
+ 9.O7 ....
243-RT
......
4O
Figure
.20 --
0
20-Experimenfo
puted
tangent
compression.
9<n</O
•20
.40
and commoduli
n
6o
d--s/s,
.8o
I00
120
O_
c_
,s/s=p
09
Ii
O_l
00I
08
017"
0_
0
__'-00
,I
0_I
.
......
_0
. I_
uoqJ_O
...........
180
_90"
I _.0 "
,,
........
u
u
11
II
u
/#
ii
#
_gO
I@0
l_90"
<_g'O'
/_.co"
_0"
u
J.
0
sl
II
o
c_
6
Z
0
z
n
.!
.,j
_,_
,,
o
_
--
s#
#i
/#
II
...........
ii
cr
ii
u
I
0_ <
_01
0_<
_9_I
Z __l
0__I
01__1
"i
i
-_
ii
1_
ii
,4--
0_
P_ZI
,,
l_-S_g
,,
,,
,.......
.
......
,,
_.Z-..q'/7_ .
,........
,,
i -SZ I/o//o-/V
0_I
,,
P_,cO" . I
I_0"0
"L/¢
qOUl
,, i _'_I
_01
l<gZI
,, 6'_/
I0_1
6__I
-moo
-uo.l.
_<_
0
[] x
,3"
Og
_ _"
0_ < +
,-,.<.,,
_O_Ol O_C< o_
I-S//o//o-IV
_01
v
i ,o/_./a do/41
tx
I
o8
I
00/
0
u
C
U
A
<
Z
.
.,
"
• /,
.
_.
ID:I.UaW
-!,.Jadx_
_
I
I<U "UOlSSaad
u! ]lnpom J,.ue6
pa.l.ndmoo
puo
. ....
- ..........
-18
e.Jn6!g
NACA
-
Technical
Note No.
902
Fig.
•i!
5O
I
I
I
qO
_, 30
_O
,-M
0
O
O
• 85 Ee
.7 Ee
,_ 20 L
l0
i
r.
I
0
• J
.OO2
•004
Strain
.OO8
•006
.
Figure
22.- Compressive
stress-strain
curve.
22