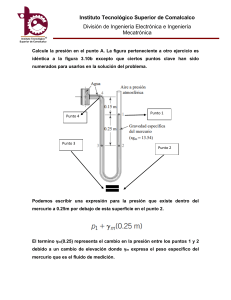
INSTITUTO MEXICANO DEL PETRÓLEO Capítulo 3 Medidores de Flujo de Presión Diferencial PLACAS DE ORIFICIO La placa de orificio es el dispositivo de medición de flujo más comúnmente usado, cuyas características son. 1. 2. 3. 4. 5. 6. Máxima pérdida de presión permanente. Más fácil de instalar. Fácilmente reproducible. Requiere inspección periódica. Es el de más bajo costo. Es el dispositivo más conocido. Este dispositivo consiste básicamente de una placa circular perforada, la cual se inserta en la tubería y presenta una restricción al paso del flujo, lo que general una presión diferencial en el sistema que resulta ser proporcional a la magnitud del flujo. La relación de proporcionalidad es del tipo cuadrática, en la que el flujo es la raíz cuadrada de la presión diferencial por una constante. El flujo al interaccionar con la restricción cambia su energía potencial (presión) por energía cinética (velocidad), describiendo un patrón de flujo muy especial que recibe el nombre de vena contracta. La expresión que define la proporcionalidad es: Q = KA h w (1) Donde: Q hw A K = = = = Flujo. Caída de presión producida por la restricción. Area de la restricción. Coeficiente de descarga del sistema. El teorema que describe el funcionamiento de la placa de orificio es el teorema de Bernoulli, donde se hace una relación entre la energía potencial, la energía cinética y las pérdidas por fracción del fluido con la tubería y la restricción. Tipo de Placas de Orificio. a) Concéntrica. Es la más común y se utiliza cuando el fluido es limpio. Cuando el fluido a medir en un líquido con gases ó cuando es un gas o un vapor con líquido, la placa tiene un pequeño orificio en la parte superior o inferior respectivamente. INSTITUTO MEXICANO DEL PETRÓLEO a1. Segmentada. El área del orificio segmentado en equivalente al área del orificio concéntrico. Se usa cuando se requiere eliminar el estancamiento de materiales extraños, instalándose con la secante horizontal y con su sección curva coincidiendo con la superficie inferior de la tubería. Es muy usada para medir vapor húmedo, líquidos con sólidos en suspensión o aceites con agua cuando la medición se hace en tubería horizontal. Cuando el orificio se puede localizar verticalmente, debe cambiarse a orificio concéntrico. a2. Excéntrica. Esta placa tiene un orificio perforado excéntrico, el cual es tangente a la superficie superior de la tubería cuando el fluido es un gas, y tangente a la superficie inferior cuando es un líquido. Esta placa tiene las mismas ventajas que la segmental. a3. Perfil Cuadrante. Esta placa es muy utilizada cuando se tienen fluidos muy viscosos. El fluido debe de ser limpio, ya que el orificio es concéntrico. Las placas de perfil cuadrante son las indicadas a medir fluidos en régimen laminar con número de Reynolds menor a 10 000 (en el flujo máximo) y mayor a los valores reportados en la Tabla 1. TABLA 1. Re Mínimo para el uso del Perfil Cuadrante. β 0.25 250 ReD 0.30 300 0.35 400 0.40 500 0.45 700 0.50 1000 0.55 1700 0.60 330 b) Placas de Perfil Cónico. Este tipo de perfil es uno de los desarrollos más recientes de las placas de orificio, se localizan cuando el número de Reynolds de un fluido es menor a los reportados en la Tabla 1 y mayor a los indicados en la Tabla 2. TABLA 2. Re Mínimo para el uso del Perfil Cónico. β ReD β ReD β ReD 0.10 0.11 0.12 0.13 0.14 0.15 25 28 30 33 35 38 40 0.17 0.18 0.19 0.20 0.21 0.22 0.23 43 45 48 50 53 0.25 0.26 0.27 0.28 0.24 60 63 65 68 70 55 0.29 73 0.16 58 0.30 75 INSTITUTO MEXICANO DEL PETRÓLEO Las placas de perfil cónico son las indicadas a medir fluido en régimen laminar con número de Reynolds mayor a 10000 (en el flujo mínimo) y mayor a los valores reportados la Tabla 3. TABLA 3. Re Mínimo para el uso del Perfil Cónico. β 0.25 ReD 250 0.30 300 0.35 400 0.40 500 0.45 700 0.50 1000 0.55 1700 0.60 330 PROCEDIMIENTO DE CÁLCULO. El procedimiento de cálculo aquí descrito está basado en las expresiones, tablas y recomendaciones descritas en el libro “Flow Meter Engineering” del autor L.K. Spink, 9ª. Edición. El procedimiento varía en función del fluido que se vaya a manejar, clasificándolos principalmente en líquidos, gases y vapores. a) Caso Líquidos. En este caso, la determinación se hará mediante el procedimiento conocido como “Método Universal”. Este método utiliza a la variable “s”, que recibe el nombre de factor de descarga, como una función de β (relación de diámetros). El factor de descarga (s) está definido mediante la siguiente expresión: S= Qmed G L ND 2 hm Ft Fa Fm Fc Fp (2) Donde: S = Factor de descarga = flujo real/flujo teórico, que pasa a través del Orificio (=) adimensional. Qmed = Gasto máximo correspndiente a la escala total del medidor, en Galones por minuto ó m3/hr. GL = Gravedad específica del fluido a 60º F. N = Constante de proporcionalidad, que depende de las unidades Usadas. D = Diámetro interno de la tubería en pulgadas o milímetros. INSTITUTO MEXICANO DEL PETRÓLEO hm = Rango diferencial ó diferencial de presión máxima del rango seleccionado en pulgadas de H2O ó mm H2O. Fm = Factor de corrección por densidad relativa del líquido de sello (elemento secundario manómetros de mercurio o medidores de campana) Fa = Factor de corrección por expansión del material de la placa. Fp = Factor de corrección por compresibilidad. Fc = Factor de corrección por número de Reynolds basada en S. Ft = Factor de corrección por temperatura. Secuencia de Cálculo. 1) Cálculo del factor de lectura en M3/HR. Considerando una escala del indicador de 0-10. Flec = Flec [=] M3/H; Qn 50 (3) Qn [=]Gal/min. Donde: Qn es el gasto normal que manejara el medidor, el cual estará indicado al 7.07 de la escala 1-10. El factor de lectura se redondea a la cifra más próxima o bien el nuevo factor de lectura será el más adecuado, escogido de acuerdo a criterios de rangeabilidad o gasto máximo deseado en la medición 2. Determinado el factor de lectura, el gasto máximo que manejará el medidor será. Q med = Flec ∗ 10 0.227125 (4) Qmed [=] GAL/MIN. 3. - Una vez calculado el gasto del medidor, hay que determinar como es comparativamente con el gasto máximo, es decir: INSTITUTO MEXICANO DEL PETRÓLEO Si Qmax < Qmed. ; continuar con el procedimiento de cálculo, si no se cumple esta condición, incrementar el factor de lectura y recalcular el gasto del medidor. 4. - Determinación de la constante de proporcionalidad “N”. Se determina por medio de la Tabla 3. 5. - Cálculo de Fm. Se determina por medio de la Tabla 4, o de la ecuación siguiente: Fm = 1 − 0.0737 ∗ Gs (5) Donde: Gs = densidad relativa del líquido de sello, cuando se usa una celda de presión diferencial como elemento transmisor, se tiene que Gs = 0 y por lo tanto Fm= 1. 6. - Determinación de Fa. Ver apéndice A. 7. - Determinación de Fp. Suponiendo Fp = 1, a menos que se maneje hidrocarburos a condiciones de presión y temperatura elevadas. Si este fuera el caso, Fp se determina mediante el procedimiento descrito en el apéndice B. 8. - Cálculo de Fc. Dado que en la ecuación (2), el factor de descarga “S” queda como función de Fc, se considera que para una estimación inicial Fc=1. 9. - Cálculo de factor Ft. Cuando se trabaja con fracciones de petróleo, el factor Ft se determina mediante el apéndice C. Para líquidos en general se utiliza la ecuación 6. Ft = Gf Gl (6) Donde: Gf = Gravedad específica del fluido A P y T de operación. 10. - Rango diferencial del medidor hm. Se propone como valor inicial 100 pulgadas de H2O. INSTITUTO MEXICANO DEL PETRÓLEO 11. - Determinación del factor de descarga “S”. Se determina con la ecuación (2). 12. - Cálculo de la β preliminar. 13. - Determinación del número de Reynolds asociado al factor Fc. Rd Ds Fm hm G f = Fc µ (9) Donde: Κ = 17920 para sistema inglés. Κ = 140 para sistema métrico Rd = Número de Reynolds. M = Viscosidad de líquido a P y T de operación en cp. hw = Diferencial de presión producida al pasar el Qn por el orificio. hw = Qn ( Qmed ) 2 hm (10) Obtenido el valor de S para el sistema en particular, la β se determina por medio del uso de las Tablas 5 o 6, o bien, se determina mediante un proceso iterativo buscando un valor de β que satisfaga alguna de las siguientes expresiones: S = 0.598 ∗ β 2 + 0.01 ∗ β 3 + 0.51804 ∗ β 6.425 (7) (Tomas en brida, en vena contracta o en esquina). S = 0.58925 ∗ β + 0.2725 ∗ β 3 + 0.51804 ∗ β 4 + 1.75 ∗ β 5 2 (8) (Tomas en tubería). 14. - Si el factor RD/Fc es mayor que 50 000, la suposición Fc = 1, es correcto y por la tanto el valor de β obtenido en el paso 12 es el adecuado, si el factor RD/Fc es menor o igual que 10 000, el régimen de flujo corresponde al patrón laminar, lo que hace INSTITUTO MEXICANO DEL PETRÓLEO necesario utilizar una placa de orificio de perfil especial, cuadrado o cónica, que dependerá del valor del número de Reynolds mínimo y del valor de la β encontrando (Ver Tablas 1 y 2). En este caso se procederá dé acuerdo con lo establecido en el paso 16. Si el valor del factor RD/Fc se encuentra entre 10 000 a 50 000, se determina un nuevo valor de (Fc), reiniciándose el procedimiento en el paso No. 11. Con el nuevo valor S se recalcula otro valor de Fc y se compara con el valor anterior de Fc; si la diferencia no es significativa, se finaliza el procedimiento. Si la diferencia es mayor A 0.01 se repite la interacción hasta que los valores coincidan. 15. - Se considera que el valor de β es correcto si se encuentra entre 0.25 y 0.70, de no ser así, se procede como sigue: a) Si β es mayor de 0.7, incrementar el hm, y reiniciar el procedimiento en el paso 11. b) Si β es menor de 0.25, decrementar el hm, y reiniciar el procedimiento del paso 11. 16. - Si el número de Reynolds es menor a 10000, junto con el valor de β obtenido, se compara con los valores de las Tablas 1 y 2; para determinar el tipo de perfil especial a usarse (cuadrante ó cónico) y se precede de la siguiente manera: a) Si el perfil es cuadrante, con el valor de S obtenido se interpola de la Tabla No. 7 los valores de β y r/ D, para así obtener el diámetro del orificio (d) y el radio del perfil cuadrante “r”. b) Si el perfil requerido es el cónico, el valor de β se encuentra mediante la siguiente ecuación: [1 + ( 0.734) ] β= 1 2 − 4 (11) S La ecuación interior es restringida para tomas en esquina y para β ≤ 0.3 Con el valor de β se obtiene el diámetro del orificio (d). INSTITUTO MEXICANO DEL PETRÓLEO INSTITUTO MEXICANO DEL PETRÓLEO INSTITUTO MEXICANO DEL PETRÓLEO CALCULO PARA MEDICORES DE FLUJO TIPO PLACAS DE ORIFICIO PARA LIQUIDOS DE A CUERDO AL METODO ITERATIVO DEL LIBRO “FLOW MEASUREMENT ENGINEERING HANDBOOK” TERCERA EDICIÓN DE R.D. MILLER . Este método esta basado principalmente en el procedimiento para el cálculo de la relación d/D llamada β para líquidos, a su vez, se calcula el diámetro de orificio de la placa corregido por coeficiente de dilatación de los materiales de la placa de orificio y de la tubería. 1. Datos generales del proceso. A. B. C. D. E. F. G. H. I. J. K. TAG: TAMAÑO DE LA LINEA: NUMERO DE LA LINEA: FLUIDO: ESTADO DEL FLUIDO: FLUJO NORMAL: PRESION: TEMPERATURA: GRAVEDAD ESPECIFICA (S.G.): VISCOSIDAD: MÁXIMA PRESION DIFERENCIAL (∆P): FE-3101/3102 6” AA 86A19 A53A / AA 86B17 A53A AGUA AMARGA LIQUIDO 91.77 m3/h = 129.38 GPM 5.6 kg/cm2 = 79.63 psig 37°C = 98.6ºF 0.98 1 CP 100 plg: H2O 2. Determinación del rango de flujo máximo del medidor. El rango de flujo máximo se determina mediante la siguiente formula: Q Q = M N Q N 50 10 = 91.77 Q M = m3 / h 91.77 50 = 129.7836m 3 / h ≅ 130m 3 / h 10 El rango de la escala o gráfica es de 0-10 raíz por lo tanto el Factor de escala o de lectura es: FL = QM 130m 3 / h = = 13m 3 / h 10 10 Se hace la conversión de m3/h a GPM (galones por minuto); INSTITUTO MEXICANO DEL PETRÓLEO 91.77 Q Q 3 m 3 1000 Lt. 1gal 1h = 91.77 (4.403) GPM × × × 3 h 3.785 Lt. 60min 1m = 404.0633 GPM N M = 130 (4.403) = 572.39 GPM Se determina la β 0 para líquidos siguiendo el procedimiento de la tabla 9.29. 3.1 De la tabla 9.23 se determina la ecuación del factor S M para líquidos por el método de la Gravedad Específica a condiciones de Flujo, esto es: SM = Fp GF NvD 2 q v hw Donde: F p = Factor de compresibilidad del Fluido G F = Gravedad Específica del fluido sin corrección por presión. q v = Rango de flujo volumétrico N v = Factor N para flujo volumétrico en GPM para gravedad específica D = Diámetro interno de la tubería corregido por factor de expansión térmica del material hw = Máxima presión diferencial del fluido 3.2 Se procede a la determinación del F p del fluido. Se expresa dicho factor mediante la ecuación 2.208; Fp = 1 + Z L pr Donde: Z L = Factor de compresibilidad líquido: Z L = 0.269Tr − 0.5163Tr2 + 0.3521Tr3 − 0.0461 p r = Presión absoluta reducida de un gas o vapor Se determinan la presión y temperaturas reducidas del Fluido (agua) pr = La P (absoluta ) PC (crítica) presión absoluta del fluido es: Pman = (5.6 Kg / cm )(14.22) = 79.63 psig ; Patm = 14.7 psia 2 Pa = 79.63 psig + 14.7 = 94.332 psia Pa = Patm + Pman ; INSTITUTO MEXICANO DEL PETRÓLEO De acuerdo a la tabla D-1, la presión crítica del agua es: 3197.9 psia Por lo tanto Tr = pr = P (absoluta ) 94.332 psia = 0.02948 = PC (crítica) 3197.9 psia T (º R ) TC (crítica ) T (ºR) = [(37 ºC) (1.8) + 32] + 460 = 577.68 ºR Tc = 1165.1 ºR según Tabla D-1 entonces: Tr = T (º R ) 558.6º R = = 0.47944; Tr2 = 0.22986 ; Tr3 = 0.1102 TC (crítica ) 1165.1º R Se procede a calcular el factor de compresibilidad líquido: Z L = 0.269Tr − 0.5163Tr2 + 0.3521Tr3 − 0.0461 Z L = 0.269(0.4794) − 0.5163(0.22986) + 0.3521(0.1102) − 0.0461 Z L = 0.00293 Se calcula el factor de compresibilidad del Fluido: F p = 1 + Z L p r = 1+ (0.00293) (0.02948) = 1.000086 Se procede a la sustitución de valores para el cálculo del Factor SM . F p = 1.000086 G F = 0.98 q v = QM = 572.39 GPM N v = 5.666455 Este factor se determina de la tabla 9.16 tomando en cuenta las unidades (GPM) y que se está calculando por medio de la ecuación de gravedad especifica para líquidos. D = FaD Dmeas ; FaD = 1 + α P (TF B.4. por lo tanto: D= 1 + (0.0000067)(98.6 − 68) [ − 68) ; α P = 0.0000067 para acero al carbón según tabla ] ( 6.065) = 6.066 “ ; D 2 = 36.79 hw = hm = ∆P = 100 pulg. H 2 O SM = 3.3 Fp GF NvD 2 q hw v = ( 1.000086 )( 0.98 )(572.39) (5.666455)(36.79)( 100 ) = 0.2718206 Se procede a la determinación de la ecuación por medio del cálculo del número de Reynolds, esto es basado en la ecuación d) de la tabla 9.20 para flujo volumétrico a condiciones de flujo por medio de la gravedad específica; INSTITUTO MEXICANO DEL PETRÓLEO Fp GF R D = 17,902.78 q v ; donde µ cP = Viscosidad del fluido = 1 CP. µ cP DN vG (1.000086)(0.98) = 17,902.78 (572.39) = 292139.6447 ; de acuerdo a la tabla 9.28 (1)(6.067)(5.666455) en la sección de placas de orificio entre bridas, si el R D > 200,000, deberá aplicarse la ec. j) para calcular la β 0 ; esto es: 0.6 2 β 0 = 1 + S M −1 / 4 ; sustituyendo valores: 2 0.6 β 0 = 1 + (0.2718206) 4 −1 / 4 = 0.558378 Una vez que se ha calculado el valor de β 0 se procede a calcular valores para β en forma iterativa hasta que β n − β n −1 < 0 ; esto se realiza siguiendo el método descrito en la tabla 9.31. De acuerdo al método; se calcula el coeficiente de descarga C C = C∞ + b R Dn Donde: C ∞ = Coeficiente de descarga a Número de Reynolds Infinito = 0.5959 + 0.0312 β 2.1 − 0.18 β 8 + 0.09 β4 β3 − 0 . 0337 D D(1 − β 4 ) b = Constante de acuerdo a la tabla 9.1 = 91.706 β 2.5 n = 0.75 Calculando el valor de C∞ : C ∞ = 0.5959 + 0.0312 β 2.1 0.5959 + 0.0312 (0.5583 ) 2.1 = 0.604005 β4 β3 − 0.18 β + 0.09 − 0.0337 D D(1 − β 4 ) 8 = 4 ( 0 . 5583 ) ( 0 . 5583 )3 − 0.18 (0.5583 ) 8 + 0.09 − 0 . 0337 (6.067 ) (6.067 )(1 − (0.5583 ) 4 ) INSTITUTO MEXICANO DEL PETRÓLEO Se calcula el factor b = 91.706 β 2.5 = 91.706(0.5583) 2.5 = 21.3583 Se sustituyen los valores en la ecuación: C = C∞ + (21.3583) b (0.604005) + = 0.605704 n = (292139.6447 ) 0.75 RD De a cuerdo al procedimiento, se calcula el primer valor iterado para por β , el cual se representa β 1 y se expresa por la ecuación: CY 2 β n = 1 + 1 S M −1 / 4 Sustituyendo valores: CY 2 β 1 = 1 + 1 S M −1 / 4 0.605704 2 = 1 + 0.2718206 −1 / 4 = 0.639866 ( Y1 = 1 para líquidos) Se hace la diferencia; esto es: (0.558378) – (0.639866) = 0.08148 > 0.0001; se continuo con las iteraciones. Se calcula el valor de C ∞ con el valor de β 1 C ∞ = 0.5959 + 0.0312(0.6398) 2.1 − 0.18(0.6398) 8 + 0.09 (0.6398) 4 (0.6398) 3 − 0 . 0337 (6.067) (6.067)(1 − (0.6398) 4 ) = 0.60573 Se calcula el factor b = 91.706 β 2.5 = 91.706(0.6398) 2.5 = 30.0267 Sustituyendo los valores para la ecuación: C = C∞ + 30.0267 b 0.60573 + = 0.608119 n = (292139.6447) 0.75 RD Se sustituye el valor en la ecuación: C β 2 = 1 + S M 2 −1 / 4 Se hace la diferencia 0.608119 2 = 1 + 0.2718206 −1 / 4 = 0.638807 β n − β n −1 < 0.0001 ; esto es: (0.638807) – (0.639866) = 0.001059 > 0.0001; se continuo con las iteraciones. Se calcula el valor de C ∞ con el valor de β 2 INSTITUTO MEXICANO DEL PETRÓLEO C ∞ = 0.5959 + 0.0312(0.6388) 2.1 − 0.18(0.6388) 8 + 0.09 (0.6388) 4 (0.6388) 3 − 0 . 0337 (6.067) (6.067)(1 − (0.6388) 4 ) = 0.604598 Se calcula el factor b = 91.706 β 2.5 = 91.706(0.6388) 2.5 = 29.9095 Sustituyendo los valores para la ecuación: C = C∞ + 29.9095 b 0.604598 + = 0.606978 n = (292139.6447) 0.75 RD Se sustituye el valor en la ecuación: C β 3 = 1 + S M 2 −1 / 4 Se hace la diferencia 0.606978 2 = 1 + 0.2718206 −1 / 4 = 0.639307 β n − β n −1 < 0.0001 ; esto es: (0.639307) – (0.638807) = 0.00059 > 0.0001; se continua con las iteraciones. Se calcula el valor de C ∞ con el valor de β 3 C ∞ = 0.5959 + 0.0312(0.6393) 2.1 − 0.18(0.6393) 8 + 0.09 (0.6393) 4 (0.6393) 3 − 0 . 0337 (6.067) (6.067)(1 − (0.6393) 4 ) = 0.604594 Se calcula el factor b = 91.706 β 2.5 = 91.706(0.6398) 2.5 = 30.026 Sustituyendo los valores para la ecuación: C = C∞ + 30.026 b 0.604594 + = 0.606983 n = ( 292139.6447) 0.75 RD Se sustituye el valor en la ecuación: C β 4 = 1 + S M 2 −1 / 4 Se hace la diferencia 0.606983 2 = 1 + 0.2718206 −1 / 4 = 0.639305 β n − β n −1 < 0.0001 ; esto es: (0.639305) – (0. 639307) = 0.0000016 < 0.0001; esto es que: β 4 = β = 0.639305 5 Con este valor se procede a calcular el diámetro interno de la placa tomando en cuenta el factor de expansión del material por Temperatura: Fad = 1 + α PE (TF − 68) El valor de α PE = 0.0000096 para acero inoxidable según la tabla B.4. Entonces; INSTITUTO MEXICANO DEL PETRÓLEO Fad = 1 + (0.0000096)(98.6 − 68) = 1.00029376 Sustituyendo los datos en la ecuación para el diámetro interno de la placa: d meas = βD (0.639305)(6.067) = = 3.8775” Fad 1.00029376 De acuerdo a la figura 8.7 (según ANSI 2530 y ASME fluid meter 1971) el elemento primario se debe instalar en un tramo recto de tubería de 7D de longitud aguas arriba y 3.5D aguas abajo.