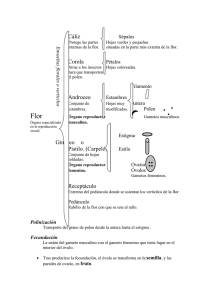
TALLER DE APLICACIÓN - ESTADÍSTICA II NOTA: Para que un punto sea válido debe tener justificación con los procedimientos vistos en clase 1. Para el siguiente enunciado justifique su respuesta. En la prueba de hipótesis Ho: µ ≥ 200 con S2 = 36 y n = 26 se obtuvo un promedio igual a 198 entonces: a) Siempre se rechaza c) Ho se rechaza al 5% e) (c) y (d) b) Se comete error tipo I de 0,06 d) Ho no se rechaza al 1% f) Ninguna de las anteriores 2. Los meteoritos se clasifican en petrosos o ferrosos según su composición. Los primeros, difíciles de identificar si no se recogen inmediatamente después de su caída, se caracterizan por estar compuestos, entre otros elementos, por un 36% de oxígeno, un 23% por hierro, un 18% de silicio y un 14% de magnesio y 9% de otros elementos. Seguido el rastro luminoso de un meteorito, se acudió al lugar en donde, al parecer, había caído descompuesto en muchos fragmentos a causa del impacto con el suelo. Recogidos 200 de estos fragmentos de la zona en cuestión se obtuvieron los siguientes porcentajes de elementos en los doscientos fragmentos recogidos: 34% de oxígeno, 24% de hierro, 17% de silicio, 15% de magnesio y 10% de otros elementos. A la vista de los datos obtenidos ¿puede concluirse que el meteorito observado era de tipo petroso? Use un error tipo I de 5%. 3. Los cinco estudiantes más pilosos de estadística II se asocian y montan una fábrica ensambladora de autos deportivos. Una de sus prioridades para ser más competitivos, y mejorar los ingresos operacionales, es reducir el tiempo de secado de una pintura. Se prueban dos fórmulas de pintura; la fórmula 1 tiene el contenido químico estándar y la fórmula 2 tiene un nuevo ingrediente secante que tiende a reducir el tiempo de secado. De la experiencia se sabe que la desviación estándar del tiempo de secado es ocho minutos y esta variabilidad inherente no debe verse afectada por la adición del nuevo ingrediente. Se pintan 25 autos con la fórmula 1 y otros 25 con la fórmula 2 con tiempos promedio de secado de 116 minutos para la fórmula 1 y 112 minutos para la fórmula 2. ¿A qué conclusión pueden llegar sobre la eficacia del nuevo ingrediente, al nivel de significancia de 0,05? 4. Laura, quien realizo un curso por internet de clarividente, ha pronosticado, que, en unillanos, el nivel de abstención en las próximas elecciones para decano será del 40% como máximo. Se elige al azar una muestra aleatoria de 200 estudiantes, con derecho a voto, 75 de los cuales estarían dispuestos a votar. Con un nivel de significación del 1%, usted que puede decir acerca del pronóstico de la clarividente de Laura. 5. Con un mayor nivel de significancia la probabilidad de rechazar una hipótesis nula que en realidad sea verdadera: a. b. Permanece inalterada Disminuye c. d. Aumenta Cualquiera de las anteriores e. Ninguna de las anteriores 6. Andrés se presentó a una convocatoria en las Naciones Unidas, como no paso, consiguió trabajo en una estación de gasolina. El avispado de Andrés se inventó un aditivo para mejorar el rendimiento de los vehículos. Primero realizó una muestra de 36 vehículos y encontró que el consumo medio fue de 9.7 km/l, con una desviación estándar de 0.9km/l, mientras que el consumo medio de otra muestra de 32 vehículos aumento a 10.1 Km/l con una desviación estándar de 0.85 km/l al emplear el aditivo. ¿Cómo le resulto el invento de Andrés? Use un nivel de significancia del 0.05 7. Ud como profesional en mercadeo trabaja en una empresa fabricante de productos informáticos de consumo y desea saber si los defectos por cada laptop provienen de una distribución de Poisson, para lo cual selecciona 300 laptops de forma aleatoria y registra el número de defectos por aparato. Use un alfa de 0,05 No. de defectos No. de laptops 0 213 1 41 2 18 ≥3 28 8. Ana María es contratada por Bill Gates para que dirija el departamento de control de calidad de una empresa que monto en San Juanito. Con el fin de disminuir la proporción de piezas en mal estado que produce cierta máquina, Ana hace algunos ajustes al proceso de producción, ella quiere determinar si estos cambios sí reducen sustancialmente la proporción de artículos defectuosos del proceso. Para ello, toma una muestra de 200 artículos del proceso original, y encuentra 24 piezas en mal estado, y examina 150 artículos del nuevo proceso y observa 6 piezas defectuosas. ¿Cree Usted que los cambios efectuados al proceso, por Ana, han reducido el porcentaje de artículos defectuosos? Use un nivel de confianza del 95%. 9. En un experimento, realizado por un grupo de investigación conformado por estudiantes del programa de Agronomía de Unillanos, relativo al cruce de dos híbridos de especies de flores se obtuvo el resultado que se indica a continuación ¿son estos resultados consistentes con la relación esperada 9:3 3:1? Use ∝= 0.05. Flor magenta, estigma verde 120 Flor magenta, estigma rojo 49 Flor roja, estigma verde 36 Flor roja, estigma rojo 12 10. El PREU, para conocer el impacto de la pandemia en la comunidad estudiantil, basándose en el registro de notas de la oficina de admisiones, observo que en el segundo semestre del año 2019 de 4000 estudiantes de la FCE. 3200 aprobaron todas las materias inscritas, 400 aprobó la mitad, 240 reprobó todas las materias y 160 se retiró. Al final del semestre pasado el PREU seleccionó a 600 estudiantes de la misma facultad con los siguientes resultados: 380 aprobaron todas las asignaturas, 78 aprobaron la mitad, 105 reprobaron todas las asignaturas y 37 se retiraron. ¿A qué conclusión debe llegar la directora del PREU? ¿Cree usted que la pandemia, y por ende la virtualidad, afecto en algo el rendimiento académico? Alfa = 0,01