ISFD 807
ANÁLISIS MATEMÁTICO
Prof. Mat.
TRABAJO PRÁCTICO N° 0 – DIAGNÓSTICO
Ej. 1 Resolver las siguientes inecuaciones, expresar el intervalo real y graficar en la recta real
a) 5x – 4 ≥ 6
c) 2 · ( x – 5 ) ≤ 8 – 4x
b) 1 – 12x + 9 < 6
d) -0,5 · ( x – 2 ) > 0,5 · ( 4x + 6 )
2
Ej. 2 Dada la función lineal 𝑓(𝑥) = 5 𝑥 + 1 ,
a)
b)
c)
d)
graficar aplicando el método de la pendiente.
Escribir la ecuación que representa a las infinitas funciones paralelas a f.
Dar la ecuación de la recta perpendicular a f que pasa por el punto (2,– 5)
¿El punto P (5, 6) pertenece a la gráfica de f?
Ej. 3 En un mismo sistema de ejes cartesianos graficar f (x) = 4 – x2, g(x) = 2x + 1 y la recta
vertical x = 3. Indicar las coordenadas de los puntos de intersección y sombrear las regiones
encerradas.
Ej. 4 Usando algún graficador, representar las siguientes funciones elementales:
1
a) 𝑓(𝑥) = 2 𝑥 + 1
i) 𝑦 = √𝑥
b) 𝑦 = 𝑥 2 + 𝑥 − 6
c) 𝑔(𝑥) = 𝑥 3 + 3𝑥 2 − 4𝑥
j) 𝑓(𝑥) = √𝑥
k) 𝑦 = |𝑥|
d) 𝑦 = 2𝑥
l) 𝑦 =
e) 𝑦 = 𝑒 𝑥
f) 𝑦 = 𝑙𝑜𝑔2 𝑥
m) 𝑦 = 𝑠𝑒𝑛 𝑥
n) 𝑦 = cos 𝑥
−𝑥
o) 𝑓(𝑥) = {
1 − 𝑥2
3
g) 𝑦 = log 𝑥
1
𝑥
𝑠𝑖 𝑥 < −1
𝑠𝑖 𝑥 ≥ −1
h) ln 𝑥
Ej. 5 Determinar el dominio de cada función.
𝑥+1
e) 𝑦 = ln(𝑥 2 − 9)
a) 𝑦 = 𝑥 2 +𝑥−2
4
3
b)
𝑓(𝑥) = 𝑥 2 +1
f) 𝑦 = √𝑥 2 + 𝑥
c)
𝑔(𝑥) = √2𝑥 + 7
g)𝑦 = 𝑥 5 + 2𝑥 3 − 𝑥 2 + 4
d)
𝑦 = 𝑒 𝑥−5
h) 𝑦 = 2 𝑥
1
2−𝑥
Ej. 6 Considerar la función 𝑓(𝑥) = {𝑥 + 2
1
𝑥
,
,
,
𝑥 < −1
− 1 ≤ 𝑥 < 1. Graficar e indicar su dominio
𝑥>1
Ej. 7 Dada la composición 𝑓 = 𝑔 ° ℎ se pide identificar las funciones 𝑔 y ℎ.
1) 𝑓(𝑥) = (𝑥 + 5)2
3
2) 𝑓(𝑥) = √cos 𝑥
TP N° 0
3) 𝑓(𝑥) = 3 ∙ 𝑥 − 3
1
4) 𝑓(𝑥) = ln 𝑥
Página 1
ISFD 807
ANÁLISIS MATEMÁTICO
Prof. Mat.
Ej. 8 Para el gráfico dado, indicar: Dominio, Imagen, Intersección con los ejes (o.o. y raíces),
F(1), F(2), puntos máximos y mínimos, intervalos de crecimiento y decrecimiento, intervalos
de positividad y negatividad.
Ej. 9 Teniendo en cuenta la definición formal de límite:
lim 𝑓(𝑥) = 𝐿
𝑥→𝑥0
↔
∀𝜀 > 0 ∃ 𝛿 > 0 / 𝑠𝑖 |𝑥 − 𝑥0 | < 𝛿 → |𝑓(𝑥) − 𝐿| < 𝜀
Se pide identificar del gráfico 𝑥0 , 𝜀, 𝛿 y 𝐿.
Ej. 10 Calcular, si existe, el valor del límite:
3𝑥
a) lim𝑥→+∞ 𝑥+5
2𝑥 2 −10𝑥+8
𝑥−4
𝑥 2 +9
lim𝑥→−∞ 𝑥 2 −7
2𝑥 2 −1
lim𝑥→+∞ 𝑥 2 −3𝑥
b) lim𝑥→4
c)
d)
TP N° 0
𝑥−9
e) lim𝑥→9 𝑥−3
√
𝑥 2 −𝑥−2
f) lim𝑥→2− (𝑥−2)2
|𝑥|
g) lim𝑥→0 𝑥
h) lim𝑥→0 𝑓(𝑥);
𝑓(𝑥) = {
𝑥+1
1 − 𝑥2
, 𝑥<0
, 𝑥≥0
Página 2
ISFD 807
ANÁLISIS MATEMÁTICO
Prof. Mat.
Ej. 11 Bosquejar la gráfica de una función 𝑓(𝑥) que cumpla simultáneamente las siguientes
condiciones:
𝐷𝑜𝑚 (𝑓) = [0; 3) ∪ (3; +∞)
𝑂𝑟𝑑𝑒𝑛𝑎𝑑𝑎 𝑎𝑙 𝑜𝑟𝑖𝑔𝑒𝑛 𝑒𝑛 𝑒𝑙 𝑝𝑢𝑛𝑡𝑜 (0, 4)
𝑅𝑎í𝑧 𝑑𝑜𝑏𝑙𝑒 𝑥1 = 𝑥2 = 2; 𝑅𝑎í𝑧 𝑠𝑖𝑚𝑝𝑙𝑒 𝑒𝑛 𝑥3 = 5
lim𝑥→3− 𝑓(𝑥) = 2 y lim𝑥→3+ 𝑓(𝑥) = −∞
lim𝑥→+∞ 𝑓(𝑥) = 1
Ej. 12 Esbozar una función con dominio todos los reales, que presente una discontinuidad no
evitable en 𝑥 = – 4 y una discontinuidad evitable en 𝑥 = 2
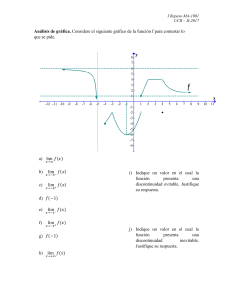
Ej. 13 Para el gráfico dado, analizar y clasificar la continuidad en los puntos:
𝑥0 = −3;
𝑥1 = 2;
𝑥2 = 5
y
𝑥3 = 6
Ej. 14 Estudiar la continuidad en R, clasificar y verificar gráficamente (usar graficador)
a) 𝑦 =
2
𝑥−1
b) 𝑦 = ln(𝑥 − 2)
c) 𝑦 =
𝑥 2 −4
𝑥−2
Ej. 15 Determinar el valor del parámetro 𝒂, de modo que 𝑓(𝑥) = {
d) 𝑦 = {
𝑥2
3
, 𝑥≤1
, 𝑥>1
1 − 𝑥2 , 𝑥 ≤ 2
sea
𝑥+𝒂 , 𝑥 >2
continua en 𝑥 = 2.
TP N° 0
Página 3