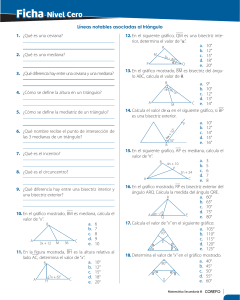
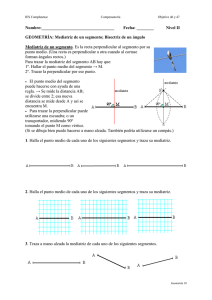
̅̅̅̅̅ = 𝟐𝟎 𝒚 𝑷𝑵 ̅̅̅̅̅ = 𝟏𝟖, la bisectriz del ángulo exterior M determina Ejercicio 7: En el triángulo MNP, es 𝑴𝑷 sobre la semirrecta ̅̅̅̅̅ 𝑷𝑵 𝒆𝒍 𝒑𝒖𝒏𝒕𝒐 𝑸 𝒅𝒆 𝒎𝒂𝒏𝒆𝒓𝒂 𝒒𝒖𝒆 ̅̅̅̅̅ 𝑵𝑸 = 𝟏𝟒 . Hallar 𝑴𝑵 Este ejercicio se resuelve con el Teorema de la Bisectriz externa. Son todas propiedades o teoremas. Grafico el problema: Tengo UNA INCOGNITA: Calcular el segmento MN. El teorema de la bisectriz de un ángulo externo (en cualquier tipo de triángulos) plantea que existe una razón matemática entre los las originales del ángulo y los segmentos en los cuales divide la bisectriz al lado opuesto. Para poder aplicar esta propiedad me faltaría poder encontrar PQ para poder plantear el esquema de razones que plantea este teorema. Yo se que PQ = PN + NQ, y como se que PN = 18 y NQ = 14 con lo cual los sumo y obtengo que PQ = 32 Entonces: Lado MP = 20 cm Lado MN = INCÓGNITA Segmento PQ = 32 cm Segmento NQ = 14 cm Resolvemos: 𝑀𝑃 𝑃𝑄 = 𝑀𝑁 𝑁𝑄 20 32 = 𝑀𝑁 14 Despejo MN 20 ∗ 14 = 𝑀𝑁 32 𝟖, 𝟕𝟓 = 𝑴𝑵