INSTITUTO TECNOLOGICO SUPERIOR DE COATZACOALCOS
Docente: Ing. Tadeo Urbina Gamboa
Tema: Problemario UNIDAD 2
Materia: Algebra lineal
Carrera: Ingeniería Eléctrica
Grado: 3°er semestre
Grupo: BE
Alumnos: Rendón De Los Santos Bryan
De La Cruz Zempoaltecatl Jairo Daniel
Hernández Reyes José David
López Flores Julio Gabriel
06/agosto/2024
INTRODUCCION
Las matrices son una de las estructuras más fundamentales en matemáticas y tienen aplicaciones
extensivas en diversas áreas de la ciencia y la ingeniería. Se pueden considerar como una extensión
natural de los números y los vectores, proporcionando una forma sistemática de organizar y
manipular datos en múltiples dimensiones.
Las matrices son una herramienta matemática poderosa que facilita el manejo y la interpretación
de datos en múltiples dimensiones. Imagina las matrices como una forma de organizar información
de manera ordenada, similar a cómo una hoja de cálculo organiza datos en filas y columnas. Esta
organización es crucial para resolver problemas complejos en diversas áreas del conocimiento.
El álgebra matricial es una rama de las matemáticas que se enfoca en el estudio y la manipulación
de matrices y sus propiedades. Esta disciplina proporciona un marco formal para manejar sistemas
lineales, transformar datos y resolver problemas en diversas áreas de la ciencia y la ingeniería.
Desarrollo:
Las matrices son estructuras matemáticas fundamentales que se utilizan en una variedad de
campos, desde la ingeniería hasta la economía y la informática.
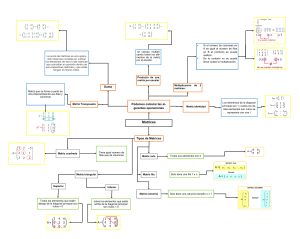
1. Definición y Notación
•
Definición: Una matriz es una tabla rectangular de números, símbolos o expresiones,
dispuestos en filas y columnas. Los números en una matriz se llaman elementos.
•
Notación: Una matriz se denota generalmente con una letra mayúscula (por ejemplo, AAA)
y sus elementos se indican con dos subíndices (por ejemplo, aija_{ij}aij, donde iii es el índice
de la fila y jjj es el índice de la columna).
2. Tipos de Matrices
•
Matriz Fila: Una matriz de una sola fila.
•
Matriz Columna: Una matriz de una sola columna.
•
Matriz Cuadrada: Una matriz con el mismo número de filas y columnas.
•
Matriz Diagonal: Una matriz cuadrada en la que los elementos fuera de la diagonal principal
son cero.
•
Matriz Identidad: Una matriz diagonal especial en la que todos los elementos de la diagonal
principal son uno.
•
Matriz Transpuesta: Una matriz obtenida al intercambiar filas por columnas de la matriz
original.
3. Operaciones con Matrices
•
Suma: Se realiza sumando los elementos correspondientes de dos matrices del mismo
tamaño.
•
Multiplicación: Se lleva a cabo multiplicando matrices siguiendo reglas específicas, donde
el elemento cijc_{ij}cij de la matriz resultante es la suma del producto de los elementos
correspondientes de las filas y columnas.
•
Determinante: Un valor escalar asociado a una matriz cuadrada que proporciona
información sobre ciertas propiedades de la matriz, como si es invertible.
•
Inversa: Una matriz que, cuando se multiplica por la matriz original, da la matriz identidad.
Solo las matrices cuadradas que tienen un determinante distinto de cero tienen inversa.
4. Teoremas y Propiedades
•
Teorema de Cayley-Hamilton: Toda matriz cuadrada satisface su propio polinomio
característico.
•
Propiedad de la Matriz Inversa: Una matriz cuadrada AAA es invertible si y solo si su
determinante no es cero.
•
Teorema de la Descomposición: Cualquier matriz cuadrada puede ser descompuesta en
una matriz triangular superior y una triangular inferior (de composición LU), o en productos
de matrices ortogonales y diagonales (de composición en valores singulares).
5. Aplicaciones
•
Sistemas de Ecuaciones Lineales: Las matrices se usan para representar y resolver sistemas
de ecuaciones lineales.
•
Transformaciones Lineales: Las matrices pueden representar transformaciones en el
espacio, como rotaciones y escalados.
•
Cálculo de Algoritmos: En algoritmos de gráficos por computadora, redes neuronales y
muchas otras áreas de la informática.
6. Teoría Avanzada
•
Espacios Vectoriales: Las matrices están estrechamente relacionadas con los espacios
vectoriales y las transformaciones lineales en ellos.
•
Teoría de la Representación: En álgebra abstracta, las matrices se usan para representar
elementos de grupos y álgebra.
•
Matemáticas Aplicadas: En análisis numérico y estadística, las matrices se utilizan para
técnicas como la regresión y el análisis de componentes principales.
Las matrices son una herramienta poderosa en matemáticas y sus aplicaciones, y su estudio abarca
tanto conceptos fundamentales como teorías avanzadas que tienen profundas implicaciones en
diversas disciplinas.
¿Qué es el Álgebra Matricial?
El álgebra matricial es la parte del álgebra lineal que se ocupa de las matrices y sus operaciones. Al
igual que el álgebra clásica se enfoca en números y ecuaciones, el álgebra matricial se enfoca en
matrices y operaciones asociadas como la suma, la multiplicación, y la inversión. La capacidad para
trabajar con matrices permite la solución de sistemas de ecuaciones lineales, la transformación de
espacios y la representación de relaciones en múltiples dimensiones.
2. Componentes Básicos
•
Matrices: Son arreglos rectangulares de números dispuestos en filas y columnas. Cada
elemento en una matriz se identifica por su fila y columna. Por ejemplo, una matriz AAA de
tamaño m×nm \times nm×n se representa como:
a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots
& \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \]
•
Operaciones Básicas:
o
Suma: Se realiza sumando los elementos correspondientes de dos matrices de igual
tamaño.
o
Multiplicación: Implica un proceso más complejo, donde cada elemento de la matriz
resultante se obtiene al realizar productos escalares entre filas y columnas.
o
Transposición: Consiste en intercambiar las filas por las columnas, obteniendo así
una matriz transpuesta.
o
Determinante: Es un valor escalar que se asocia a las matrices cuadradas y ofrece
información sobre propiedades importantes como la invertibilidad.
o
Inversa: La matriz inversa de una matriz cuadrada AAA es aquella que, cuando se
multiplica por AAA, da como resultado la matriz identidad.
3. Teoremas y Propiedades Clave
•
Teorema de la Inversa: Una matriz cuadrada AAA es invertible si y solo si su determinante
es diferente de cero.
•
Teorema de la Descomposición: Cualquier matriz cuadrada puede descomponerse en
productos de matrices especiales, como la descomposición LU (matriz triangular inferior y
superior) o la descomposición en valores singulares (SVD).
•
Propiedades de las Operaciones: El álgebra matricial estudia cómo se comportan las
matrices bajo distintas operaciones, como la conmutatividad y la asociatividad en la suma y
la multiplicación.
4. Aplicaciones del Álgebra Matricial
El álgebra matricial tiene numerosas aplicaciones prácticas:
•
Sistemas de Ecuaciones Lineales: Permite la resolución eficiente de sistemas de ecuaciones
utilizando métodos como la eliminación de Gauss.
•
Transformaciones Geométricas: En gráficos por computadora, las matrices transforman
objetos en 2D y 3D, permitiendo rotaciones, escalados y traslaciones.
•
Machine Learning: En aprendizaje automático, las matrices se utilizan para representar y
manipular datos, ajustar modelos y realizar cálculos en redes neuronales.
•
Control de Sistemas: En ingeniería, las matrices se utilizan para modelar y analizar sistemas
dinámicos y de control.
En el ámbito de la ingeniería
El álgebra lineal es una rama fundamental de las matemáticas aplicadas que tiene
una gran importancia en la ingeniería eléctrica. A través de sus conceptos y
técnicas, el álgebra lineal permite resolver problemas complejos relacionados con
la electricidad y el magnetismo.
En primer lugar, el álgebra lineal se utiliza en el análisis de circuitos eléctricos.
Mediante la representación matricial de los componentes y las leyes fundamentales
de la electricidad, es posible analizar y resolver ecuaciones que describen el
comportamiento de los circuitos. Esta herramienta permite diseñar sistemas
eléctricos eficientes y confiables.
Además, el álgebra lineal es esencial para el estudio de los sistemas de control en
la ingeniería eléctrica. Los sistemas de control se utilizan para regular y mantener
el funcionamiento correcto de los sistemas eléctricos, desde pequeños dispositivos
electrónicos hasta grandes redes de distribución de energía. El álgebra lineal
proporciona herramientas para modelar y analizar los sistemas de control, como la
transformada de Laplace y la teoría de matrices. Por otro lado, el álgebra lineal es
fundamental en el procesamiento de señales eléctricas.
En la ingeniería eléctrica, se trabaja con señales analógicas y digitales que
contienen información relevante. El álgebra lineal permite representar y manipular
estas señales mediante técnicas como la transformada de Fourier y la convolución.
El álgebra lineal desempeña un papel crucial en la ingeniería eléctrica al
proporcionar herramientas y técnicas para el análisis y diseño de circuitos eléctricos,
sistemas de control y procesamiento de señales. Su comprensión y aplicación
adecuada son necesarias para el éxito en esta disciplina.
Definición de matrices
Una matriz es un conjunto de números reales, que están dispuestos en «m»
filas y en «n» columnas:
A los números que forman la matriz se les llama elementos.
El número de filas por el número de columnas se denomina dimensión de la
matriz y se designa como m x n, siendo m el número de filas y n el número de
columnas.
Por ejemplo, estas son matrices de diferentes dimensiones:
Donde la matriz A es una matriz de 2×3 (2 filas y 3 columnas), la matriz B es
una matriz de 3×2 (3 filas y 2 columnas) y la matriz C es una matriz de 3×3 (3
filas y 3 columnas).
Las matrices son utilizadas en el álgebra lineal, una de las ramas del álgebra.
Algunos tipos de matrices:
Matriz rectangular
Es aquella que tiene distinto número de filas que de columnas (m≠n):
Matriz fila
Es toda matriz rectangular que tiene una sola fila (m = 1).
Matriz columna
Es toda matriz rectangular con una columna (n = 1).
Matriz opuesta
La matriz opuesta a otra matriz es la que tiene todos los elementos de signo
contrario a la matriz original. Por ejemplo, si tenemos la matriz A:
Su matriz opuesta sería:
La matriz opuesta a A se designa como -A, donde que todos los elementos
son de signo contrario a los elementos de la matriz A.
Matriz traspuesta
Se llama matriz traspuesta de una matriz cualquiera de dimensión m x n a la
matriz que se obtiene al convertir las filas en columnas. Se representa con el
superíndice «t»y su dimensión es por tanto n x m.
Por ejemplo, tenemos la siguiente matriz A, de dimensión 2 x 3 (2 filas y 3
columnas):
Su matriz traspuesta, designada con el superíndice «t», se obtiene
convirtiendo las filas en columnas. Por tanto, la primera fila de la matriz A,
formada por los elementos 1, -3 y 0, pasa a ser la primera columna de su matriz
traspuesta. De la misma forma, la segunda fila de la matriz A, formada por los
elementos 2, 4 y 1, pasa a ser la segunda columna de su matriz traspuesta:
La dimensión de la matriz traspusta de A es de 3 x 2 (3 filas y 2 columnas):
Matriz cuadrada de orden n
Una matriz cuadrada es aquella que tiene igual número de filas que de
columnas (m = n). En este caso, la dimensión se denomina orden, cuyo valor
coincide con el número de filas y de columnas.
Por ejemplo, la siguiente matriz es una matriz cuadrada de orden 3, ya que
tiene 3 filas y 3 columnas:
Entre los elementos de las matrices cuadradas suelen tenerse muy en cuenta
los que forman las diagonales de la matriz.
Así, se llama diagonal principal de una matriz cuadrada a los elementos que
componen la diagonal que va desde la esquina superior izquierda, hasta la
esquina inferior derecha:
Se llama diagonal secundaria de una matriz cuadrada a los elementos que
componen la diagonal que va desde la esquina superior derecha, hasta la
esquina inferior izquierda:
Matriz triangular superior
Es toda matriz cuadrada donde al menos uno de los términos que están por
encima de la diagonal principal son distintos de cero y todos los términos
situados por debajo de la diagonal principal son ceros:
Normalmente, cuando se dice que hay que triangular la matriz, se refiere a
que hay que hacer ceros los elementos que quedan por debajo de la diagonal
principal.
Matriz triangular inferior
Es toda matriz cuadrada donde al menos uno de los términos que están por
debajo de la diagonal principal son distintos de cero y todos los términos
situados por encima de la diagonal principal son ceros:
Matriz diagonal
Es toda matriz cuadrada en la que todos los elementos que no están
situados en la diagonal principal son ceros:
Matriz escalar
La matriz escalar es toda matriz diagonal donde todos los elementos de la
diagonal principal son iguales:
Matriz identidad
Es la matriz escalar cuyos elementos de la diagonal principal valen uno, es
decir, la diagonal principal está formada por 1, y el resto de los elementos son
0:
Matriz nula
La matriz nula donde todos los elementos son cero. Suele designarse con un
0:
Ya estás más familiarizado con las matrices. Si quieres seguir aprendiendo
cómo operar con matrices o cómo obtener la inversa de una matriz, te
recomiendo el Curso de Matrices, donde te lo explico todo paso a paso.
Operación entre matrices
Suma de matrices
Dadas dos o más matrices del mismo orden, el resultado de la suma es otra
matriz del mismo orden cuyos elementos se obtienen como suma de los
elementos colocados en el mismo lugar de las matrices sumando.
Ejemplo:
Resta de matrices
Dadas dos o más matrices del mismo orden, el resultado de la resta es otra
matriz del mismo orden cuyos elementos se obtienen como la resta de los
elementos colocados en el mismo lugar de los matrices sumandos.
Ejemplo:
Multiplicación por un número
Para multiplicar una matriz cualquiera por un número real, se multiplican todos los
elementos de la matriz por dicho número.
Ejemplo:
Producto de matrices
El resultado de multiplicar dos matrices es otra matriz en la que el elemento que
ocupa el lugar cij se obtiene sumando los productos parciales que se obtienen al
multiplicar todos los elementos de la fila “i” de la primera matriz por los elementos
de la columna “j” de la segunda matriz. Es decir, multiplicamos la primera fila por
los elementos de la primera columna y el resultado será nuestro nuevo elemento.
Para ello, el número de columnas de la primera matriz debe coincidir
con el de filas de la segunda. Si no fuese así no podríamos realizar la
operación.
Ejemplo:
Observamos como la matriz resultante tiene el número de filas de la primera y el
de columnas de la segunda.
Debemos recordar, que las matrices no tienen la propiedad conmutativa. En el
caso de que se pudiera operar A.B y B.A el resultado por lo general puede ser
diferente.
Ejercicios resueltos:
Regla de sarrus
Su determinante se calcula mediante la llamada regla de Sarrus:
Regla mnemotécnica: la regla de Sarrus parece complicada,
pero si os fijáis bien, también estamos multiplicando diagonales.
Observando los siguientes dos ejemplos, os quedará más claro:
Ejemplo 1
Regla de cramer:
Solución:
La matriz de coeficientes del sistema es
La matriz de incógnitas es
La matriz de términos independientes es
Calculamos el determinante de AA:
Podemos aplicar la regla de Cramer.
La primera incógnita es xx, cuyos coeficientes son los de la
primera columna de AA. La matriz A1A1 es como AA pero
cambiando dicha columna por la columna BB:
Calculamos xx:
La segunda incógnita es yy y sus coeficientes son los de la
segunda columna de AA. Tenemos que calcular el determinante
de la matriz
Calculamos yy:
Por tanto, la solución del sistema es
1)
(−20) − (−80) = 88
2)
−1
𝐴
3)
4)
−2/7
= [ 3/7
46/105
−1/14
5/14
151/420
0
0 ]
1/6
5)
6)
7)
8)
9)
10)