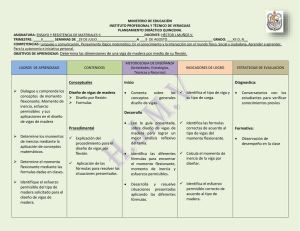
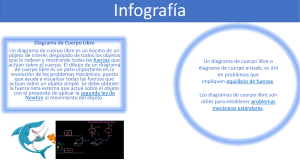
Tarea 08 Alumno: Vergara Alonso Jesus Ricardo Efectos Pδ y PΔ, Introducción a los momentos de segundo orden. Si se considera tres miembros prismáticos idénticos AB de longitud L y rigidez a la flexión El que están simplemente apoyados en sus extremos, como se muestra en la figura 1. El miembro mostrado en la figura 1a está sujeto a momentos de extremo M°, iguales y opuestos, mientras que el miembro de la figura 1b está sujeto, además de a los momentos de extremo M, a fuerzas axiales de compresión P que actúan en los extremos A y B. Por último, el miembro mostrado en la figura 1c está sujeto a cargas de tensión axiales 7 que actúan en los extremos A y B. Figura. 1 Momentos de primer orden Al considerar el equilibrio de los momentos de todas las fuerzas que actúan sobre el miembro AB, tomados alrededor de cualquier apoyo, se encuentra que las reacciones RB y RA son cero para los tres miembros bajo estudio. Al tomar en cuenta el equilibrio de momentos alrededor del punto D representa la sección localizada a la distancia z del origen, y el punto C es la sección en el centro del claro. ∑(𝑀)𝐷 = 0; 𝑀0 − 𝑀𝑧 = 0; 𝑀𝑧 = 𝑀0 El diagrama de momento flexionante, válido para los tres miembros, se muestra en la figura. 1d. Observe que hemos considerado el equilibrio del segmento AD en su estado no deformado (sin deflexión). A estos cálculos se les conoce como cálculos de primer orden. A los momentos calculados bajo esta suposición se les conoce como momentos de primer orden; y a las deflexiones correspondientes se les conoce como deflexiones de primer orden. Al momento flexionante adicional Pu, causado por la interacción de la carga axial y la deflexión se le conoce como momento secundario. El momento flexionante en cualquier punto es Mz. Este momento flexionante de segundo orden se encuentra al sumar el momento primario al secundario en ese punto. Su variación a lo largo de la vigaFigura. 2 Momento de segundo orden columna se muestra en la figura 2. En la figura 3, la intersección de la vertical en A con la tangente que parte de C es decir A/C es igual a la deflexión 8 en el centro. Si se denota con A, el área del diagrama M/EI debida al momento flexionante de primer orden, y con As, el área del diagrama M/EI debido a cualquier momento flexionante secundario, se deduce del teorema 2 de área-omento que: Figura 3. Deflexiones centrales de una viga, una vigacolumna y un miembro sujeto a flexión y tensión. 𝛿𝑜 = 𝐴𝑓𝑧1 𝛿∗ = 𝐴 𝑧 + 𝐴 𝑧 = 𝛿𝑜 + 𝐴 𝑧 𝑐 𝑓 1 𝑠𝑐 2 𝑠𝑐 2 𝛿1∗ = 𝐴𝑓𝑧1 − 𝐴𝑠𝑟𝑧2 = 𝛿𝑜 − 𝐴𝑠𝑟𝑧2 A partir de la construcción mostrada en la figura 3, la intersección de la vertical en A con la tangente que parte de C es decir A/C es igual a la deflexión 8 en el centro. Si se denota con A, el área del diagrama M/EI debida al momento flexionante de primer orden, y con As, el área del diagrama M/EI debido a cualquier momento flexionante secundario.