Del modelo atómico de Bohr al modelo de la mecánica cuántica.
Anuncio

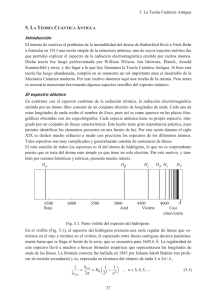
Del modelo atómico de Bohr al modelo de la mecánica cuántica.El éxito sonado de Bohr para explicar cómo sería un átomo se verá frenado por las dificultades que presentaba su modelo para explicar los átomos polielectrónicos. A ello se le unía el inconveniente de que mezclaba dos físicas para explicar el comportamiento del átomo de hidrógeno, la física clásica (Newtoniana, aplicable al mundo macroscópico y determinista, usada en su primer postulado) con la física cuántica (ideas de Planck, cuantización de la energía, en los otros dos).Aportaciones ilustres como la de De Broglie, proponiendo que los electrones se podían comportar como ondas, o la de Heisemberg, para asegurar que no es posible conocer simultáneamente la posición y la velocidad de una partícula del mundo atómico (cosa que si es posible en nuestro mundo macroscópico) harán que la nueva explicación de cómo sería un átomo venga del libro de la física cuántica, no determinista y sí probabilística, por lo que la idea de conocer en todo momento la trayectoria del electrón sería abandonada y el término órbita sería reemplazado por el término orbital.La necesidad de un nuevo modelo se hace patente cuando los hechos experimentales no pueden ser explicados con las ideas del modelo de Bohr. Los espectroscopios de mayor poder resolutivo confirmaron que los espectros atómicos poseían una estructura fina: hablamos de nuevas líneas espectrales. Imagen del libro de la editorial Oxford Así, las líneas originales resultaron ser realmente varias (multipletes) y se pudieron explicar con la aportación de Sommerfeld: las órbitas permitidas por Bohr podrían ser circulares y elípticas (modelo Bohr-Sommerfeld) y en cada una el electrón se movía con una energía ligeramente distinta. Quedarían representadas mediante un segundo nº cuántico (l), que podría tomar valores desde 0 a n-1, siendo n el nº cuántico principal. Por ejemplo, para n = 3 aparecían realmente tres líneas, correspondientes a valores de l=0,1,2. (Observa el gráfico) No tardaría en llegar más desdoblamientos de las líneas espectrales, sobre todo en presencia de campos magnéticos externos. Sería llamado efecto Zeeman: explicado por las distintas orientaciones que podrían adquirir esas órbitas elípticas, quedando éstas recogidas en un tercer nº cuántico ml. (nº cuántico magnético). Si este número cuántico toma valores de -l,...,0,...+l, quedarían identificadas el número de líneas aparecidas en los espectros. Por último, Uhlenbeck y Goudsmit observan que cada una de las rayas del espectro realizado bajo un intenso campo magnético y medidas con potentes espectroscopios eran en realidad un doblete. Confirman la hipótesis de Stern y Gerlach, quienes sugirieron que el pequeño campo magnético del electrón puede sumarse o restarse al campo externo, por lo que la energía de la línea sería ligeramente distinta en uno u otro caso. Proponen un nuevo nºcuántico (ms,, nº cuántico de spin) que tomará únicamente dos valores posibles: +1/2 o -1/2. Y ahora, ¿qué modelo atómico nos podrá explicar estos hechos experimentales? Al ser considerado el electrón como onda se le asocia una ecuación de ondas para conocer la energía de los niveles permitidos (ecuación de Schrödinger), cuya solución dependerá de tres variables (tres números cuánticos), es decir, que cada estado energético permitido vendrá caracterizado por tres números cuánticos. Sus soluciones son aproximadas y su cuadrado da idea de la probabilidad de encontrar el electrón de un átomo. Como esta solución aproximada se consigue dando unos valores a variables de la ecuación y que precisamente coinciden con los mismos números cuánticos introducidos de manera experimental para explicar los espectros, viene a ser un modelo más que fiable para conocer cómo son finalmente los átomos.Estas soluciones, dadas a partir de la combinación de tres números cuánticos, constituirán un orbital, zona de alta probabilidad de encontrar al electrón. Observa la fotocopia donde se muestra la función de probabilidad frente a la distancia al núcleo. Con ella podemos deducir la forma de los orbitales (s,p,d) y la diferencia de tamaño entre orbitales de mismo valor del segundo número cuántico (ejm:1s, 2s, 3s) Efecto de apantallamiento del electrón.Un electrón de un átomo polielectrónico no recibe íntegramente la fuerza de atracción electrostática del núcleo puesto que hay electrones más internos que lo apantallan, por lo que quedará atraído por el núcleo con una carga menor que Z, lo que se denomina carga nuclear efectiva. Cuanto menor es la carga nuclear con la que un electrón “ve” al núcleo (carga nuclear efectiva menor), más pequeña es la atracción del electrón por el núcleo y, por tanto, más alta es la energía del orbital en el que se encuentra el electrón. Este motivo justifica el orden que presentan los distintos subniveles de energía a la hora de realizarse su llenado y concretar la configuración electrónica del elemento. Observa en el gráfico que la energía de los distintos subniveles cambia con el número atómico, es decir, varía ligeramente para cada elemento y que en resumen quedan ordenados como aparece en el diagrama de Moeller (regla de la lluvia). Image n del libro de SM