Pistas sobre los Trabajos Prácticos 2010
Anuncio
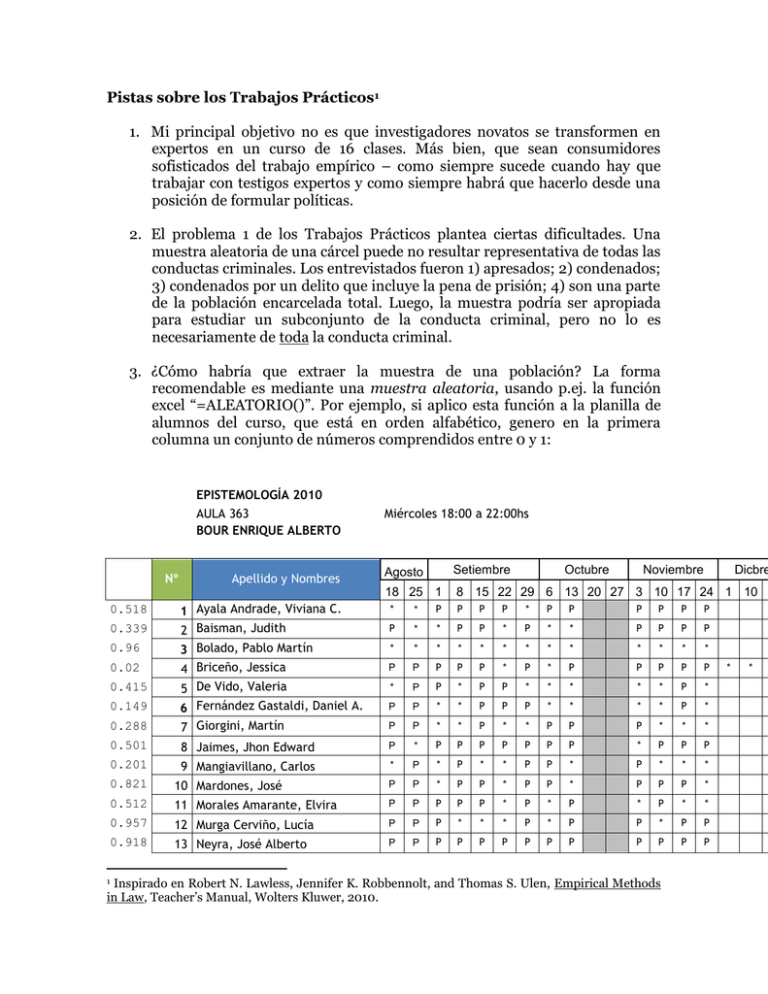
Pistas sobre los Trabajos Prácticos1 1. Mi principal objetivo no es que investigadores novatos se transformen en expertos en un curso de 16 clases. Más bien, que sean consumidores sofisticados del trabajo empírico – como siempre sucede cuando hay que trabajar con testigos expertos y como siempre habrá que hacerlo desde una posición de formular políticas. 2. El problema 1 de los Trabajos Prácticos plantea ciertas dificultades. Una muestra aleatoria de una cárcel puede no resultar representativa de todas las conductas criminales. Los entrevistados fueron 1) apresados; 2) condenados; 3) condenados por un delito que incluye la pena de prisión; 4) son una parte de la población encarcelada total. Luego, la muestra podría ser apropiada para estudiar un subconjunto de la conducta criminal, pero no lo es necesariamente de toda la conducta criminal. 3. ¿Cómo habría que extraer la muestra de una población? La forma recomendable es mediante una muestra aleatoria, usando p.ej. la función excel “=ALEATORIO()”. Por ejemplo, si aplico esta función a la planilla de alumnos del curso, que está en orden alfabético, genero en la primera columna un conjunto de números comprendidos entre 0 y 1: EPISTEMOLOGÍA 2010 AULA 363 BOUR ENRIQUE ALBERTO Nº 0.518 0.339 0.96 0.02 Apellido y Nombres 1 Ayala Andrade, Viviana C. 2 Baisman, Judith 3 Bolado, Pablo Martín 4 Briceño, Jessica Miércoles 18:00 a 22:00hs Agosto Setiembre 18 25 1 8 15 22 29 6 13 20 27 3 10 17 24 1 10 * Octubre Noviembre Dicbre * P P P P * P P P P P P P * * P P * P * * P P P P * * * * * * * * * * * * * P P P P P * P * P P P P P * P P * P P * * * * * P * 0.149 5 De Vido, Valeria 6 Fernández Gastaldi, Daniel A. P P * * P P P * * * * P * 0.288 7 Giorgini, Martín P P * * P * * P P P * * * 0.501 8 Jaimes, Jhon Edward P * P P P P P P P * P P P 0.201 9 Mangiavillano, Carlos * P * P * * P P * P * * * P P * P P * P P P * 0.415 0.821 10 Mardones, José P P * 0.512 11 Morales Amarante, Elvira P P P P P * P * P * P * * 0.957 12 Murga Cerviño, Lucía P P P * * * P * P P * P P 0.918 13 Neyra, José Alberto P P P P P P P P P P P P P Inspirado en Robert N. Lawless, Jennifer K. Robbennolt, and Thomas S. Ulen, Empirical Methods in Law, Teacher’s Manual, Wolters Kluwer, 2010. 1 * * 0.402 14 Oderigo, Romualdo P * * P 0.388 15 Perozo S., Jesús R. P * P P P P * * * P P * P P P P P * P * P P P * * P P * * * P P 0.26 16 Santambrogio, Alejandro P P * 0.761 17 Sanz, Javier P * P P P P P * P P P * P 0.908 18 Trovato, Agustina * P P P * P P P P P * P P 0.048 19 Zapata R., Alexander P P * P P P P P P P P P * Fecha de examen: 15 de diciembre - 16:00hs - Aula 363 [1] Fecha de examen: 1 de diciembre 9:00hs en FIEL 2 Con estos números, podemos practicar un nuevo ordenamiento de los alumnos. Curiosamente, Jessica resulta la primera alumna de la lista (ella también fue la primera en rendir examen). No son recomendables métodos que den lugar a sesgos sistemáticos (por ejemplo, tomar a los 10 primeros de la lista, o sacando los nombres de una urna). 4. El problema 3 discute el uso que hace la Corte Suprema de US de los datos sobre daños punitivos de Exxon Shipping Co. v. Baker, 128 S. Ct. 2605 (2008). Este punto puede ser apreciado en el artículo de internet híperlinkeado. La Corte usa una tabla de un trabajo previo de dos de estos autores, haciendo hincapié en dos características, a saber que la relación promedio de daño punitivo a indemnización compensatoria es muy superior a la relación mediana, y que el desvío estándar es elevado. Expresa que “aún para quienes carecemos de formación estadística, el mensaje resulta claro: el margen es elevado, y los casos atípicos someten a los demandados a daños punitivos que empequeñecen las correspondientes compensaciones. La distribución de las primas es más estrecha, pero aún así es notable, en materia de daños punitivos evaluados por los jueces: la relación promedio es 0.66:1, y el desvío estándar es 4.54.” El margen es preocupante porque con anterioridad la Corte había sostenido que los daños punitivos deben mantener una relación con las indemnizaciones, debido a lo cual finalmente impuso una regla ad hoc de 1:1 entre los daños compensatorios y los daños punitivos en los casos de naufragios marítimos. Por consiguiente, la Corte redujo la penalidad por daños punitivos de Exxon a consecuencia de derrame de petróleo del Exxon Valdez desde una cifra de $2.500 millones de dólares hasta $500 millones. En resumen, Eisenberg, Heise y Wells demostraron que la Corte no tomó en cuenta la distribución de los datos según surgen de la Tabla 2. Ésta muestra relaciones elevadas de daños punitivos a compensatorios cuando las indemnizaciones son inferiores a $1,000. El valor absoluto de estas compensaciones es bastante bajo, y en cualquier caso dentro de la categoría entran pocos casos. Se trata de outliers que afectan de manera desproporcionada los cálculos de media y de desvío estándar sobre los que está basada la Corte. 5. El ejercicio siguiente presupone un pleito de un paciente que toma una medicación y con una prueba clínica. Los pacientes que tomaron la medicación resultaron tres veces más propensos a desarrollar una enfermedad hepática, pero el resultado sólo es significativo al 20%. Se pide al estudiante que reflexione acerca del significado del p-valor y de la significación estadística en cuestión. En primer lugar, es importante tener en cuenta qué no es un p-valor. Por ejemplo, no se trata de la probabilidad de que el resultado sea meramente al azar. Un pvalor es la probabilidad de observar el dato dada la hipótesis nula de que no existe relación entre las variables medidas. Esta diferencia es importante. Podría ser que el resultado no fuera aleatorio, y aún así que la hipótesis nula sea verdadera. También es necesario entender que la inversa de un p-valor no es la probabilidad de que la hipótesis alternativa sea verdadera. Por el hecho de decir que el p-valor es del 20% no estamos diciendo que existe un 80% de probabilidad de que la hipótesis alternativa tiene una probabilidad del 80% (la hipótesis de que la medicina fue causante de los trastornos hepáticos). Para apreciar este punto, puede ser necesario recurrir a explicaciones alternativas – tales como errores de medición o la omisión de algunas variables. El trabajo práctico 5 es útil para tener cierta práctica en leer e interpretar una tabla de resultados de una regresión. En primer término, se pide que el estudiante considere si cada variable independiente es continua o binaria. La edad es, por supuesto, continua; el género, una variable binaria; el nivel educativo es una variable categórica (observen que se usan dos variables dummy para representar a tres categorías – sin diploma secundario, con diploma secundario pero sin diploma universitario, y diploma universitario); si las actitudes fueron medidas antes o después de su reacción a los estudios (binaria); si los resultados de la investigación tendían a favorecer a los liberales o a los conservadores (por ejemplo, un estudio que halló que el control de armas es efectivo fue codificado como a favor de los liberales, mientras que un estudio que determinó que la pena capital es efectiva fue codificado como favoreciendo a los conservadores) (manipulación experimental) (binaria); actitud del individuo hacia la cuestión analizada (continua); un índice de apareamiento de actitudes que mide si la actitud del individuo es consistente o no con los hallazgos del estudio (lo que codificamos como 0 si no hay apareamiento, es decir el resultado del estudio fue inconsistente con la respuesta del individuo a la cuestión, y 1 si hay apareamiento – es decir, la respuesta de quien responde fue consistente con su actitud); una medición de la identificación de quien responde con un partido político (una escala de 5 puntos; tratada como si fuera continua); un índice de apareamiento entre la ideología de quien responde y los resultados generales del estudio (que codificaremos como -1 si no hay apareamiento – es decir, una ideología inconsistente con los resultados del estudio; como +1 si hay apareamiento – es decir, ideología consistente con los resultados del estudio; y 0 para los que se auto-identifican como moderados); un índice de identificación de quien responde con un partido político (una escala de 7 puntos, tratada como continua); un índice de apareamiento entre el partido político de quien responde y los resultados generales del estudio (que codificaremos como -1 si no hay apareamiento – es decir, un partido político inconsistente con los resultados del estudio; como +1 si hay apareamiento – es decir, partido político consistente con los resultados del estudio; y 0 para los que se auto- 3 identifican como independientes). Cada una de estas variables independientes permite revisar los desafíos enfrentados a la hora de medir y codificar. Se pide a continuación que el estudiante compare su predicción con los resultados de las tablas. Resulta útil darse cuenta de que las tablas presentan los resultados de 5 análisis de regresión. ¿En qué difieren estas regresiones? Por ejemplo, el Modelo 1 hace más énfasis en variables básicas como las demográficas y dos variables de manipulación experimental (a saber, si el estudio rechazó la hipótesis nula y si el estudio mostró una tendencia a favor de liberales o de conservadores). Ahora cabe identificar qué variables tienen efectos estadísticos significativos. Por ejemplo, hay un efecto estadísticamente significativo del hecho de poseer un título secundario sobre el escepticismo – los que carecen de diploma secundario se muestran más escépticos sobre los resultados de la investigación. En los Modelos 3 y 5, se observa un efecto de la ideología y de la interacción (apareamiento) entre ideología y hallazgos del estudio. Es decir, los liberales fueron más escépticos que los conservadores y los que respondieron fueron más escépticos cuando el hallazgo era inconsistente con sus posiciones ideológicas. Finalmente, se pregunta acerca de la bondad del ajuste de los modelos. Aquí se pueden señalar los coeficientes R2 al final de la tabla. En los Modelos 1 y 4, son cero. En los Modelos 2,3, y 5, los R2 son muy reducidos pero significativos, lo que implica que las variables de los modelos explican una baja proporción de la variación observada en el escepticismo, pero que con todo son significativas2. 2 La tabla del Problema 5 sirve para discutir el problema de significatividad estadística de los coeficientes. Por ejemplo, las siguientes variables lo son: “No HS diploma” en el Modelo 1 (B=0.23*) y el efecto “Research findings favor liberals?” del Modelo 2 (B=0.17*). Estas variables pueden servir para discutir una regla que es de amplia aplicación aunque no necesariamente sea estrictamente precisa ni fiable en cada situación: un coeficiente que sea mayor que dos veces el valor absoluto de su error estándar es genéricamente significativo al 5%. Ver Robert J. MacCoun and Susannah Paletz, Citizens’ Perceptions of Ideological Bias in Research on Public Policy Controversies, Political Psychology, Vol. 30, No. 1, 2009. 4











