Ejercicio_1

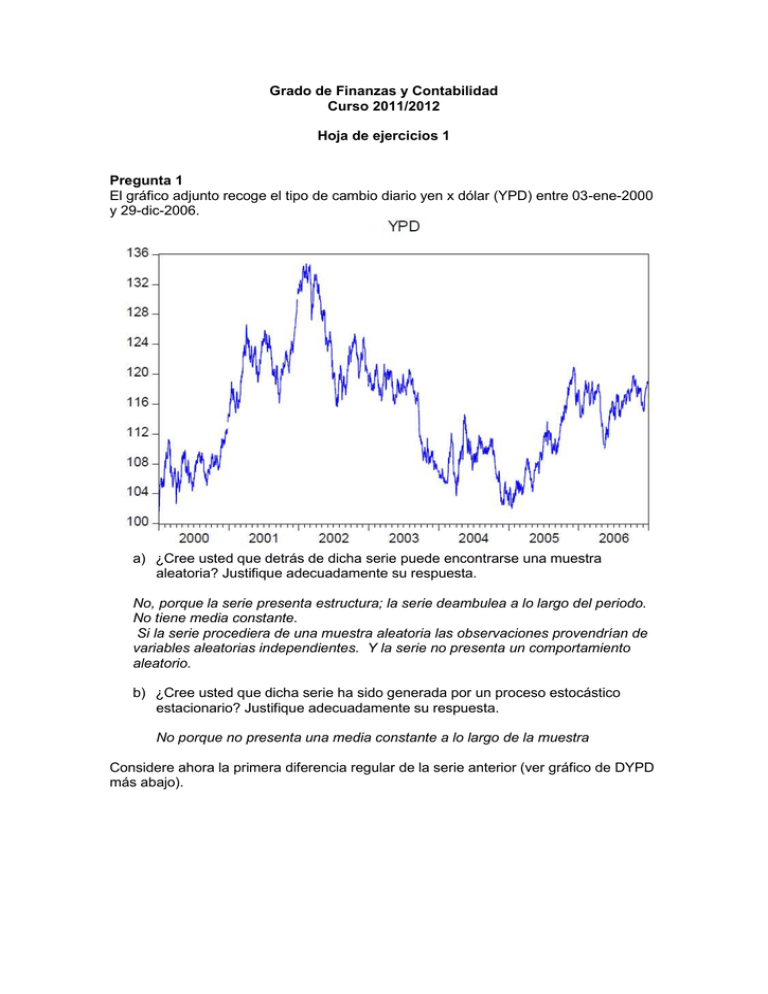
Grado de Finanzas y Contabilidad
Curso 2011/2012
Hoja de ejercicios 1
Pregunta 1
El gráfico adjunto recoge el tipo de cambio diario yen x dólar (YPD) entre 03-ene-2000
y 29-dic-2006.
a) ¿Cree usted que detrás de dicha serie puede encontrarse una muestra
aleatoria? Justifique adecuadamente su respuesta.
No, porque la serie presenta estructura; la serie deambulea a lo largo del periodo.
No tiene media constante.
Si la serie procediera de una muestra aleatoria las observaciones provendrían de
variables aleatorias independientes. Y la serie no presenta un comportamiento
aleatorio.
b) ¿Cree usted que dicha serie ha sido generada por un proceso estocástico
estacionario? Justifique adecuadamente su respuesta.
No porque no presenta una media constante a lo largo de la muestra
Considere ahora la primera diferencia regular de la serie anterior (ver gráfico de DYPD
más abajo).
c) Opine sobre la adecuación de la transformación.
Con la primera diferencia se ha obtenido estacionariedad en media, ya que
todos los valores oscilan en torno a un valor constante a lo largo de la muestra.
d) Proponga, según estime oportuno, argumentos a favor o en contra de
modelizar la no estacionariedad de la serie original con elementos
deterministas.
La estimación de la no estacionariedad con elementos determinístico no
permite modelizar adecuadamente dicho comportamiento, ya se trate de un
polinomio en el tiempo de orden 1 o superior.
Esta serie ha sido generada por un proceso estocástico. No presenta un
comportamiento determinístico
e) El correlograma de la serie diferenciada se muestra más abajo. A partir de este
se propone el siguiente modelo
donde
es un ruido blanco. ¿Considera el modelo propuesto válido?
El correlograma refleja que se puede aceptar estadísticamente la hipótesis nula
de que las correlaciones para los distintos retardos son iguales a la cero, tanto
de forma independiente, es decir, para cada retardo, como conjuntamente (los
valores de la Q son menores que los valores críticos en tablas; la χ2 igual a 50
aprox.).
Las distintas correlaciones muestrales se hallan dentro del intervalo de
confianza.
Pregunta 2
Considere el logaritmo de las exportaciones de España a EEUU mostrada en el
gráfico, junto a una tendencia lineal estimada y los residuos de dicha estimación.
a) ¿Cree que la serie original fue generada por un proceso estacionario?
No, la serie presenta un claro comportamiento alcista lo que implica que no
existe una media constante a lo largo del periodo considerado.
Por otra parte, tampoco presenta estacionariedad en la parte estacional. Tal
como refleja el gráfico, se observa claramente un comportamiento intraanual
que se repite cada año (los meses de agostos presentan significativas caídas,
por ejemplo). Por tanto la media de los meses no es constante.
b) ¿Le parece apropiado la tendencia lineal que se ha ajustado? ¿Qué estructura
plenamente estocástica propondría para la tendencia de dicha serie?
No es apropiada la tendencia lineal, pues como se observa en el gráfico la
serie residual no se ha logrado una media constante. No se ha logrado eliminar
la no estacionariedad en la parte regular..
c) Proponga de forma argumentada una transformación estacionaria que elimine
todos los aspectos de evolutividad en el nivel medio que aparecen en la serie.
Las transformaciones que habría que realizar son: una diferencia regular y una
diferencia estacional. La primera permite alcanzar estacionariedad en la parte
regular y la segunda elimina la diferencia de medias entre los meses, es decir,
la no estacionariedad en la parte estacional:
(1-L)(1-L12 ) log Xt
Pregunta 3
Considere una variable anual, sobre la cual haya que tomar una diferencia regular
para convertirla en estacionaria. Igualmente, considere que el modelo de la serie
estacionaria es un proceso autorregresivo de primer orden.
(1-0.6L) Δ log yt = at
Derive el modelo de la tasa de crecimiento. Y expréselo en términos de un proceso de
medias móviles. ¿Qué propiedad cumple el proceso para poderse expresar como
dicho proceso?
1.- el modelo de la tasa de crecimiento sería:
(1-0.6L) Tasa de crecimiento = at
2.- Denominemos Wt a la tasa de crecimiento:
Wt - 0.6W t-1 = at
Wt = 0.6W t-1 + at
W t-1= 0.6 W t-2 + a t-1
W t= 0.6 (0.6 W t-2 +a t-1)+ a t= 0.62 W t-2+0.6 a t-1+ at
W t-2= 0.6 W t-3+ a t-2
Wt= 0.62 (0.6 W t-3 + a t-2) +0.6 a t-1+ a t=
=0.63 W t-3 +0.62 a t-2+ 0.6 a t-1+ a t
Wt= 0.6t W0 + (at +0.6a t-1+ 0.62 a t-2+……+ 0.6t-1 a1)
3.- Para que un proceso autorregresivo se pueda expresar como una media móvil, es
necesario que el parámetro sea menor que la unidad, como es este caso. Es estacionario
Pregunta 4
Considere el siguiente modelo para la serie mensual
donde
es un proceso ruido blanco, y por tanto tiene media cero y varianza
una constante que se sabe que su valor cumple con la condición
y c es
.
a) Si c =0, la serie
es estacionaria.
Es falsa porque la serie y no es estacionaria ya que ha sido necesario tomar una
primera diferencia regular para conseguir la estacionariedad o constancia en media.
b) La serie
sigue un paseo aleatorio con constante si c ≠ 0. Es decir,
I(1,1) y el componente estocástico estacionario es ruido blanco.
es
Verdadera. La serie sigue un paseo aleatorio con deriva. Un paseo aleatorio es un
proceso en el que tras tomar una primera diferencia sobre la serie original se obtiene
un proceso ruido blanco. Si el modelo incluye una constante, se dice que presenta una
deriva.
c) La serie
tiene media igual a c.
Verdadera.
E(
) = E (c) + E ( at ) = c
d) La tasa de crecimiento anual media de
es del c·100%.
Verdadera, la tasa de crecimiento media es igual a c. La primera diferencia del
logaritmo de una serie es aproximadamente igual a la tasa de crecimiento. Y su
esperanza es la media que se ha calculado en el epígrafe anterior.
e) La varianza de
es
.
Verdadero.
Var (
) = var (c) + var (at )=
Pregunta 5
Considere la serie temporal
.
con el siguiente correlograma:
Señale cuáles de las siguientes afirmaciones son ciertas:
a) El estadístico Q-Stat correspondiente a la fila 36 que toma el valor 80.903 sirve para
contrastar la hipótesis nula de que las primeras 36 autocorrelaciones son iguales a
cero.
Verdadero, el estadístico Q sirve para contrastar la significatividad conjunta para
distintos retardos.
b) La correlación en la muestra entre
e
(o autocorrelación de primer orden) es
mayor que entre
e
(o autocorrelación de segundo orden).
Verdadera, en un proceso estacionario a medida que la distancia temporal entre las
variables aumenta disminuye la correlación. El presente depende del pasado cada vez
con menos intensidad.
En un proceso autorregresivo de primer orden la correlación es igual a φk , a medida
que aumenta k disminuye la correlación serial.
Podría ocurrir, en algún caso, que la correlación de orden dos fuese superior a la de
orden uno, seguramente porque estaría reflejando un comportamiento cíclico
relevante.
En todo caso, el presente correlograma refleja que la correlación de primer orden es
superior a la de segundo orden.
c) La autocorrelación de quinto orden es estadísticamente significativa.
Falsa, la autocorrelación de quinto orden no es significativa, porque su estimador
muestral se halla dentro de las bandas de confianza.
Las bandas del correlograma reflejan la varianza del estimador bajo la hipótesis nula
de que el verdadero parámetro es igual a cero. En este caso el valor del estimador
muestral es menor
d) Si
se sitúa por encima de la media de la muestra,
debajo de ésta.
tiende a situarse por
Falso. La correlación de primer orden en positiva, lo que indica que a un valor por
encima de la media tenderá a seguirle un valor igualmente por encima de la media.
e) La serie
es ruido blanco.
Falso. El correlograma tiene estructura y las autocorrelaciones hasta de tercer orden
son estadísticamente significativas.
Un proceso ruido blanco presenta incorrelación serial. El estadístico Q permite
rechazar la hipótesis nula de independencia serial. En este caso, dicho estadístico es
superior al valor en tablas, lo que nos lleva a rechazar incorrelación serial (líneal)
NO CONFUNDIR FUNCION
CORRELOGRAMA
DE
AUTOCORRELACION
(FAC)
CON
Pregunta 6
Considere el siguiente modelo para las ventas anuales de una empresa durante el
periodo 1985-2004.
Δ Log z t = 0.06 + 0.04 Dt 1995 + at
Donde T es la variable tiempo, at es un proceso ruido blanco y Dt 1995 es una
variable tipo escalón que toma valor 0 entre 1985 y 1994 y 1 a partir de 1995.
Señale la/las afirmaciones correctas y falsas, justificando la respuesta de todas ellas.
a) El nivel de las ventas presenta un comportamiento tendencial creciente.
Verdadera, la serie necesita una primera diferencia regular y además en el modelo hay
una constante. Indicativos de que la serie presenta una tendencia con crecimiento
sistemático.
b) En el período 1985-2004 las ventas tienen un crecimiento medio anual del 6%.
Falsa, hay que tener en cuenta la variable dummy.
E (Δ Log z t)= E(0.06 )+ E(0. 04 Dt 1995) + E(at)=
= 0.06+ 0.04 Dt 1995
c) En el período 1995-2004 las ventas tienen un crecimiento medio anual del 4%.
Falsa, es igual al 10%.
d) En el período 1995-2004 las ventas tienen un crecimiento medio anual superior al
del período 1985-1994.
Verdadera, en el primer periodo es del 6% y en el segundo del 10%
e) En el período 1995-2004 el crecimiento de las ventas tiene una media anual del
10%.
Verdadera.