guia 1 los nmeros reales
Anuncio

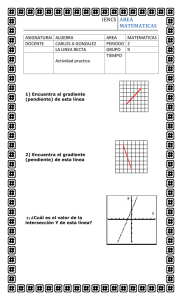
IENCS ASIGNATURA DOCENTE GUIA 1 DESEMPEÑO AREA MATEMATICAS 2015 ALGEBRA CARLOS A GONZALEZ Reconocer las propiedades de los números reales y realizar operaciones con la aplicación de sus propiedades AREA PERIODO GRUPO TIEMPO MATEMATICAS 1 8 Los números reales El conjunto formado por los números racionales Q e irracionales I es el conjunto de los números reales, se designa por Con los números reales podemos realizar todas las operaciones, excepto la radicación de índice par y radicando negativo, y la div isión por cero. a/0 4 √−4 La recta real IENCS AREA MATEMATICAS 2015 Representación de los números reales L o s núm er o s r ea les pue de n se r r e pr e se ntado s e n la r e cta co n tanta apr o xi mació n co mo q u e r amo s, pe r o hay caso s e n lo s que po de mo s r e pr e se ntar lo s de fo r ma e xacta. Ejercicios S e ñ a la e n cad a caso e l n ú me ro real al qu e co rre sp on d e la re p re sen t ación gr á f ica d ad a. Ob serva e l pu nt o gris. IENCS AREA MATEMATICAS 2015 Tomamos un cuadrado de lado 1. Entonces, usando el teorema de Pitágoras sabemos que su diagonal mide En efecto, pues 12 + 12 = d2, de donde, d = Basta coger esta medida y transportarla con el compás (tomando centro en 0 y con radio la diagonal de nuestro cuadrado). De este modo, representamos en la recta real el número . Tomamos un rectángulo de base 4 y lado 1. Entonces, usando el teorema de Pitágoras sabemos que su diagonal mide En efecto, pues 42 + 12 = d2, de donde, 17 = d2 y, por tanto, d = Basta coger esta medida y transportarla con el compás (tomando centro en 0 y con radio la diagonal de nuestro cuadrado). De este modo, representamos en la recta real el número Operaciones con números real es IENCS AREA MATEMATICAS 2015 P r o p i e da d e s d e l a S u ma d e n ú me r os r e al e s 1 . IN T ER N A El r e sulta do de s um a r do s núm e r o s r ea les e s o t r o núm er o r ea l . a + b + 2 . ASO C IAT IVA El mo do de agr u par lo s suma ndo s no var ía e l r e s ulta do . (a + b) + c = a + (b + c ) · 3 . C o nmutat iva: El o r de n de lo s s umando s no var í a la su ma. a + b = b + a 4 . Ele me nto ne utr o : El 0 e s e l e le me nto ne utr o de la suma po r que to d o núme r o sumado co n é l d a e l mismo núme r o . IENCS AREA MATEMATICAS 2015 a + 0 = a + 0 = 5 . Ele me nto o pue st o : Do s núme r o s so n o pue sto s si al sumar lo s o bte ne mo s co mo r e sultado e l ce r o . e − e = 0 El o pue sto de l o pue sto de un nú me r o e s igual al mismo núme r o . − (− ) = Dife r e ncia de nú me r o s r e ale s L a d ifer enc ia d e do s núme r o s r e ale s se de fine co mo la sum a del m in u endo m á s el o p uest o del s ust r a endo . a − b = a + (− b) Pr o ducto de nú m e r o s re ale s L a r egla de lo s signo s de l pr o d uc t o de lo s núm er o s ent er o s y r a c io na les se s igue mante nie n do co n lo s núm er o s r ea les . IENCS AREA MATEMATICAS 2015 Pr o pie dade s de l pr o ducto de nú me r o s r e ale s 1 . IN T ER N A El r e sulta do de mult ip licar do s n úme r o s r e ale s e s o tr o núme r o r e al. a b 2 . Aso ciat iva El mo do de agr u par lo s facto r e s no var ía e l r e sul tado . Si a, b y c so n n úme r o s r e ale s cuale squie r a, se cu mple que : (a b) c = a ( b c) (e ) =e · ( ) 3 . C o nmutat iva: El o r de n de lo s f acto r e s no var ía e l pr o ducto . a b= b a 4. Ele me nto ne utr o : El 1 e s el el em ent o neut r o de la m ult iplic a c ió n , po r que to do núme r o mul tip lica do po r é l d a e l mismo núme r o . a 1 =a IENCS AREA MATEMATICAS 2015 ·1 = 5 . Ele me nto o pue st o : Un núme r o e s in ve r so de l o tr o si al mu lt ipl icar lo s o bte ne mo s co mo r e sultado e l e le me nto uni d ad. 6 . Distr ib ut iva: El pr o duc to de u n núme r o po r un a suma e s i gual a la su ma de lo s pr o ducto s de dicho n úme r o po r cada uno d e lo s sumando s . a (b+ c)= a b+ a c ·(e + )= ·e + 7 . Sacar facto r co m ún: Es e l pr o ce so inv e r so a la pr o pie dad dis tr ib uti va. Si var io s s uman do s tie ne n u n fa cto r co mún, po d e mo s tr ansfo r mar la s uma e n pr o duc to e xtr aye ndo dich o facto r . a b+ a c = a ( b+ c ) ·e + = ·(e + ) D i vi si ón d e n ú mer os r e a l e s IENCS AREA MATEMATICAS 2015 L a divis ió n de do s núme r o s r e ale s se de fine co mo e l pr o ducto de l d iv i de ndo po r e l inv e r so de l diviso r . Ejercicios de la s pro pieda des de los números reales E lige la p rop ie dad de las op e racion e s con nú me ro s re ale s que se ap lica e n ca d a caso : IENCS AREA MATEMATICAS 2015