Velocidad instantánea en un movimiento circular
Anuncio

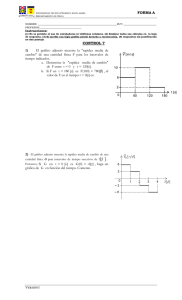
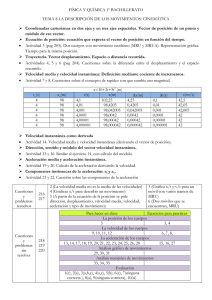
Liceo Luis Laborda Hijuelas Profesor: Francisco Soto Física I Semestre – 2013 Velocidad instantánea en un movimiento curvilíneo. Debemos recordar que la velocidad media es el cuociente entre el desplazamiento y el tiempo empleado: V X t La rapidez media es: Vm d t Cuando viajamos en un bus, y este gira bruscamente, sentimos que nuestro cuerpo sigue la misma dirección que traía el bus antes de girar, esto es por la primera ley de newton (de inercia). Esto nos dice que el vector velocidad al momento de girar tenía otra dirección que no era la del movimiento. Lo mismo sucede al amarrar un cuerpo con un hilo y lo empezamos a hacer girar. Si nos damos cuenta al soltar el cuerpo cuando lo estamos girando este sigue un movimiento en una línea tangencial a la trayectoria del círculo. De esto diremos entonces que la velocidad instantánea en un movimiento circular se representara entonces como un vector tangente a la trayectoria y la rapidez instantánea llamada también rapidez lineal. cuyo modulo será Recta Tangente Debemos recordar que una recta tangente es aquella que tota en un solo punto a una circunferencia. Además, es perpendicular al radio en dicho punto. Radio A partir de estas definiciones podemos analizar lo que sucede si representamos las velocidades a medida que nos acercamos al radio. Si los vectores están más alejados del eje de movimiento tienen un mayor modulo. Es por esto ultimo que la onda que uso David en los relatos bíblicos consistía en dos largas cuerdas de cuero que usaban para hacer girar una piedra, la que al soltar adquirirá una velocidad enorme. Aceleración en el movimiento curvilíneo. La aceleración es un vector que expresa el cambio de velocidad en el tiempo. Cuando un objeto describe un movimiento curvilíneo se dice que tiene aceleración ya que su velocidad no es constante (porque esta va cambiando de dirección a través del tiempo a medida que se desplaza). Esto ocurre aunque la rapidez sea constante. De esto último, definiremos aceleración media de la siguiente forma: v am t Donde delta v es la variación de la velocidad y delta t el intervalo de tiempo en que sucede la variación. V1 Radio V2