ppt deflexión de vigas integradoresdefinidos cálculointegral secc675
Anuncio

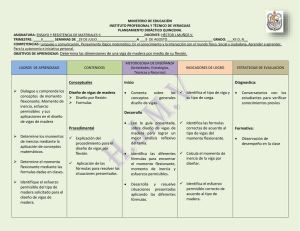
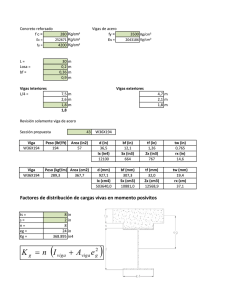
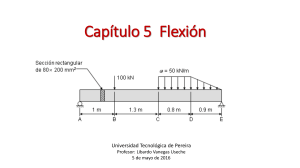
Aplicación de Integrales Deflexión de vigas, orientada a la ingeniería civil. Cálculo 1 (MAT 201) Sección: 675 Campus: Tegucigalpa M.D.C. Cátedratico: Julio César López Zerón Equipo de Trabajo: Jerson Orlando Castillo Berrios.....11411205 Jennifer Dayán Martinez Bustillo…11411081 Obdulio Jóse Ortega Juárez………….11341090 Trimestre: 3 Semestre: 2 Fecha: 13 Septiembre del 2015 INTRODUCCIÓN Al carga un cuerpo o estructura sus componentes se deforman, en las vigas sus cables se estiran y toma una forma panda o de flexión, al ocurrir esto la estructura se deforma y sus bases se desplazan, aunque estos desplazamientos son pequeños el ingeniero debe comprobar que estén dentro de los limites permitidos para asegurar que la estructura sea funcional. Estas deflexiones pueden provocar agrietamientos en paredes, techos de yeso, tuberías frágiles, desplazamiento lateral en los edificios. El cálculo de las deflexiones forma parte de procedimientos analíticos establecidos. Utilizar las integrales facilita la construcción de las ecuaciones para la deflexión y la pendiente a lo largo de la curva elástica en una viga cargada. DEFLEXIÓN FUERZA CORTANTE Y MOMENTO DE FLEXIÓN Antes hay que hablar de un componente importante ; esfuerzo que caracteriza la intensidad de la fuerza que puede aplastar, contraer o estirar una viga, causando su deformación, la cual es proporcional a la intensidad de esta. Cuando estas sobrepasan la resistencia de la viga, esta tiende a fracturarse o partirse. La fuerza cortante se desarrolla cuando las cargas externas tienden a provocar que dos segmentos de la viga resbalen y el momento de flexión es la suma de todos los momentos que actúan sobre una sección izquierda o derecha. ENUNCIADO ▪ Como se calcula la deflexión con el método de trabajo virtual: Como en el principio de conservación de energía obliga a que el trabajo virtual extremo “Wq” sea igual a la energía virtual de deformación “Uq”, ∑Qdp = 𝑥=𝐿 𝑀𝑞𝑑ⱷ, 𝑥=0 𝑑𝑥 dp = Mp 𝐸𝐼 Ecuación básica de trabajo virtual para vigas: ∑Qdp = 𝑥=𝐿 𝑀𝑝𝑑𝑥 𝑀𝑞 𝑥=0 𝐸𝐼 Q = carga virtual y sus reacciones. Dp = componentes en la dirección de la carga virtual de desplazamiento. Mq = momento producido por la carga virtual. Mp = momento producido por las cargas reales. E = modulo de elasticidad. I = momento de inercia de la sección transversal de la viga con respecto al eje centroidal. ESQUEMA DEL MODELO PROPUESTO No es posible escribir una única expresión para “Mq” y “Mp”. Por lo tanto se deben utilizar 3 integrales para calcular la energía virtual de deformación total. Se denota la región añadiendo un subíndice a la variable “X” la cual representa la posición de la sección donde se calcula el momento. Las expresiones para “Mp” y “Mq” en cada sección son las siguientes: PROCEDIMIENTO UTILIZADO ▪ Paso 1 : Para resolver el ejercicio se utiliza la formula y se sustituyen los valores. ▪ Paso 2 : Se procede a resolver la integral evaluando los limites correspondientes. ▪ Paso 3 : Luego se divide cada integral entre el momento de elasticidad “E” y el momento de inercia “I”. ▪ Paso 4 : Por último se multiplica por el factor de conversión 1728𝑃𝑢𝑙𝑔𝑎𝑑𝑎𝑠 3 para dejar el resultado expresado en pulgadas. ▪ Paso 1 : ▪ Paso 2 : ▪ Paso 3 : ▪ Paso 4 : RECOMENDACIONES • Cuando una estructura o viga se sobrecarga, al limite de sobrepasar su resistencia original o al ocurrir un sismo, la misma se deforma y sus puntos se desplazan. • El método del trabajo virtual solo es aplicable a vigas y armaduras, pues el mismo exige que los cambios en geometría sean pequeños, el mismo no podría aplicarse a un cable que experimenta un gran cambio debido a una carga concentrada. • El uso de la integral definida ayuda a encontrar la deflexión en las vigas entre un punto “a” y un punto “b” en las cuales se aplica una carga con lo que puede evitar defectos en las construcciones. • Continuar utilizando el método del trabajo virtual para calcular la deflexión de las vigas, a través de la integral definida.