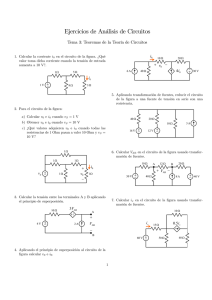
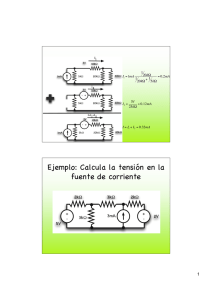
Máxima Transferencia de Potencia en circuitos AC

Máxima Transferencia de Potencia en circuitos AC
Prof. Gerardo Ceballos
∂
RTh + X Th j
A B∂A − A∂B
=
B
B2
Valor eficaz
IL =
VTh
RTh + RL + ( X Th + X L ) j
PL = I L RL
2
RL + X L j
IL
VTh
− 2 VTh RL ( X Th + X L )
2
PL =
(RTh + RL )2 + ( X Th + X L )2
2
− 2 VTh RL ( X Th + X L ) = 0
2
∂PL
=0
∂X L
[(R
[(R
Th
∂PL
∂P
=0
∂RL
Th + RL ) + ( X Th + X L
2
[(R
Th
=0
]
) ]V
+ RL ) + ( X Th + X L )
2 2
2
2
Th
VTh RL
2
X L = − X Th
− VTh RL 2(RTh + RL )
2
+ RL ) + ( X Th + X L )
2
]
2 2
(RTh + RL )2 + ( X Th + X L )2 − RL 2(RTh + RL ) = 0
2
2
RTh + 2 RTh RL + RL2 + ( X Th + X L ) − 2 RTh RL − 2 RL2 = 0
(R
Th
2
)
− RL2 + ( X Th + X L ) = 0
2
RL = RTh
Prof. Gerardo Ceballos
*
Z L = ZTh
=0
Máxima Transferencia de Potencia en AC
RTh + X Th j
VTh
IL
*
Z L = Z Th
RTh − X Th j
VTh
IL =
2 RTh
PLmax = I L RTh =
2
PLmax =
Prof. Gerardo Ceballos
VTh
2
Th
4R
VTh
2
2
4 RTh
RTh
Valor eficaz
MTP en DC vs AC
RTh + X Th j
RTh
RTh
2
p Lmax
RTh − X Th j
VTh
V
= Th
4.RTh
PLmax =
Prof. Gerardo Ceballos
VThrms
4 RTh
2
Máxima Transferencia de Potencia en DC
10‐6j Ω
10Vrms
10+6j Ω
PLmax =
Prof. Gerardo Ceballos
VTh
2
4 RTh
100
=
= 2,5w
40
Ejercicios:
Adicionalmente, hallar Z a colocar entre a y b para que reciba la máxima potencia que p
puede entregar el circuito. Hallar esta potencia media activa máxima entregada a la g
p
g
impedancia.
Prof. Gerardo Ceballos