REGLA DE BARROW
Anuncio

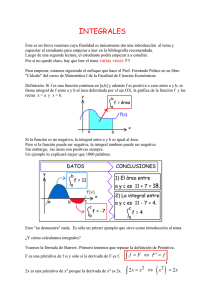
Departamento de Matemáticas REGLA DE BARROW Si f x es una función continua en a, b y F x es una primitiva de f x , entonces b a f x dx F x a F b F a b Demostración: Si F x es una primitiva de f x se verifica que d x f t dt f x dx a Supongamos que G x es otra primitiva de f x . Entonces: F ' x F x G x k Vamos a determinar k : F a 0 G a k 0 k G a F a G a k Por otro lado F b f t dt b a luego F b G b k G b G a de donde se deduce que f t dt G b G a b a C.Q.D. 1 Departamento de Matemáticas Demostraciones para E.S.O. y Bachillerato