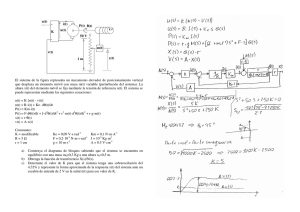
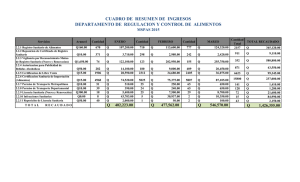
Fuerza Inerciales
Anuncio

Fuerza Inerciales Luis A. Núñez Esc. Física Universidad Industrial de Santander Velocidad angular y derivadas de vectores ûr = cos(✓(t))ı̂ + sen (✓(t))ˆ⌘
d (ûr )
d✓
˙
˙
= ✓(t) ( sen(✓(t))ı̂ + cos(✓(t))ˆ⌘) = !
~ ⇥ ûr con !
~ = ✓(t)k̂ ⌘
k̂
|
{z
}
dt
dt
û✓
⇣
⌘
⇣
⌘
d (ûr )
= ê1 ( r2 !3 ) + ê2 (!3 r1 ) = ı̂
sen(✓)✓˙ + ˆ⌘ ✓˙ cos(✓)
dt
En general para 2D dê1
dê2
˙ 3
=!
~ ⇥ ê1 y
=!
~ ⇥ ê2
con !
~ = ✓ê
dt
dt
d~c
dc1
dc2
dc3
dê1
dê2
dê3
=
ê1 +
ê2 +
ê3 + c1
+ c2
+ c3
dt
dt
dt
dt
dt
dt
dt
d~c
~c
=
+!
~ ⇥ ~c con
dt
t
~c
dc1
dc2
dc3
=
ê1 +
ê2 +
ê3
t
dt
dt
dt
2 ¿Centrífuga? 3 Velocidad angular y derivadas de vectores En general ~
~
d(·)
(·)
~
=
+!
~ ⇥ (·)
dt
t
Operador derivada vectorial ~
d(·)
2~
~
d (·)
d
(·)
dt
=
+!
~⇥
Operador segimda derivada vectorial 2
dt
⇣ t
⌘ dt ⇣
⌘
d
~
d2 (·)
=
2
dt
~
(·)
t
~
d2 (·)
=
2
dt
~
+!
~ ⇥ (·)
dt
=
~
(·)
t
~
+!
~ ⇥ (·)
t
+!
~⇥
~
(·)
~
+!
~ ⇥ (·)
t
⇣
⌘
~
~
(·)
!
~
(·)
~ + 2~! ⇥
~
+
⇥
(·)
+
!
~
⇥
!
~
⇥
(·)
t2
t
t
2
Variación del módulo del vector posición respecto al Sistema móvil Variación por rotación del sistema de coordenadas móviles 4 !
La velocidad angular y la aceleración lineal 2
d2~r
~r
!
~
~r
~a = 2 = 2 +
⇥ ~r + 2~! ⇥
+!
~ ⇥ (~! ⇥ ~r)
dt
t
t
t
Variación del módulo del vector posición respecto al Sistema móvil Variación por rotación del sistema de coordenadas móviles ~ oo0 (t) + ~
~
r 0 (t) = R
r (t)
~oo0 (t) + ~
~
v 0 (t) = V
v (t)
2
d ~rI
=
dt2
d2
⇣
⌘ Sistema NO Inercial ~ oo0 + ~r
R
2
~ oo0
~r
!
~
~r
d2 R
= 2 +
⇥ ~r + 2~
!⇥
+!
~ ⇥ (~
! ⇥ ~r) +
dt2
t
t
t
dt2
Sistema Inercial 5 ¿Fuerzas ficCcias? ¿Fuerzas no inerciales? 2
~ oo0
d2~rI0
~r
!
~
~r
d2 R
m 2 =m 2 +m
⇥ ~r + m2~! ⇥
+ m~! ⇥ (~! ⇥ ~r) +
dt
t
t
t
dt2
Supongamos que el sistema está aislado respecto a un sistema INERCIAL de coordenadas ~ oo0
~r
!
~
~r
d2 R
0=m 2 +m
⇥ ~r + m2~! ⇥
+ m~! ⇥ (~! ⇥ ~r) +
t
t
t
dt2
2
Las fuerzas que mide un sistema NO INERCIAL serán: 2
~r
m 2 =
t
!
~
m
⇥ ~r
t
Azimutal ~r
m2~! ⇥
t
Coriolis m~! ⇥ (~! ⇥ ~r)
Centrífuga ~ oo0
d2 R
dt2
Traslacional 6 Traslacionales 7 Traslacionales: Equilibrio 8 E pur si muove (1) …. 9 E pur si muove (2)…. 10 E pur si muove (3)…. 2
d2~r
~r
!
~
~r
~a = 2 = 2 +
⇥ ~r + 2~! ⇥
+!
~ ⇥ (~! ⇥ ~r)
dt
t
t
t
11 E pur si muove (3)…. 2
d2~r
~r
!
~
~r
~a = 2 = 2 +
⇥ ~r + 2~! ⇥
+!
~ ⇥ (~! ⇥ ~r)
dt
t
t
t
12 Coordenadas polares, cilíndricas y esféricas 13 Centrífuga 14 ¿Centrífuga? 15 Coriolis 2
d2~r
~r
!
~
~r
~a = 2 = 2 +
⇥ ~r + 2~! ⇥
+!
~ ⇥ (~! ⇥ ~r)
dt
t
t
t
16 Péndulo Foucault 17