1 universoexacto.com Matriz insumo
Anuncio
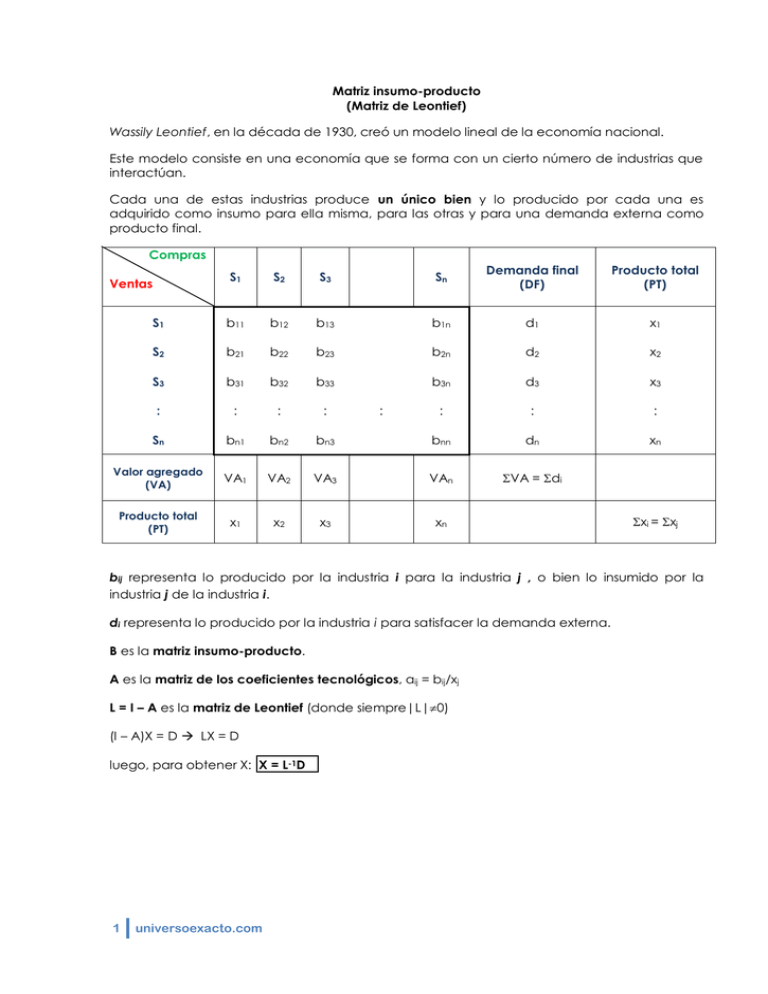
Matriz insumo-producto (Matriz de Leontief) Wassily Leontief, en la década de 1930, creó un modelo lineal de la economía nacional. Este modelo consiste en una economía que se forma con un cierto número de industrias que interactúan. Cada una de estas industrias produce un único bien y lo producido por cada una es adquirido como insumo para ella misma, para las otras y para una demanda externa como producto final. Compras S1 S2 S3 Sn Demanda final (DF) Producto total (PT) S1 b11 b12 b13 b1n d1 x1 S2 b21 b22 b23 b2n d2 x2 S3 b31 b32 b33 b3n d3 x3 : : : : : : : Sn bn1 bn2 bn3 bnn dn xn Valor agregado (VA) VA1 VA2 VA3 VAn VA = di Producto total (PT) x1 x2 x3 xn Ventas : xi = xj bij representa lo producido por la industria i para la industria j , o bien lo insumido por la industria j de la industria i. di representa lo producido por la industria i para satisfacer la demanda externa. B es la matriz insumo-producto. A es la matriz de los coeficientes tecnológicos, aij = bij/xj L = I – A es la matriz de Leontief (donde siempre|L|0) (I – A)X = D LX = D luego, para obtener X: X = L-1D 1 universoexacto.com Matriz insumo-producto (Matriz de Leontief) Ejemplo: Considera una economía hipotética de 2 industrias, S1 y S2, representada en la tabla: S1 S1 80 S2 VA S2 DF 32 0 30 40 PT PT --110 --- Determina la nueva tabla (completa) si la demanda final cambia a 42 para S 1 y 28 para S2. Solución: S1 S1 80 S2 VA 30 40 S1 110 --- S2 DF 30 40 S1 S1 80 S2 80 VA 40 PT 110 PT 32 0 PT PT --- 80 S2 VA DF 32 0 PT S1 S2 110 --- 110 --- S2 DF PT 32 0 30 110 --- 110 --- Si sumamos los elementos de esta columna obtenemos la producción total de S1 que es la misma de aquí 2 universoexacto.com La suma de estos tres elementos debe dar 110, por lo tanto el primero es 80. S1 S1 80 S2 80 VA 40 PT 200 S2 0 DF PT 32 200 30 110 --- 110 --- La suma de esta fila debe dar 200, por lo tanto obtenemos el valor de este elemento haciendo 200 – (80 + 32) = 88 S1 S2 DF PT S1 80 88 32 200 S2 80 0 30 110 VA 40 PT 200 --110 --- La suma de esta columna debe dar 110, por lo tanto obtenemos el valor de este elemento haciendo 110 – (88 + 0) = 22 Por último calculamos los totales que deben coincidir por fila y columna. S1 S2 DF PT S1 80 88 32 200 S2 80 0 30 110 VA 40 22 62 --- PT 200 110 --- 310 Una vez que hemos completado la tabla, escribimos la matriz insumo-producto: B= y con ella obtenemos la matriz de los coeficiente tecnológicos dividiendo a cada columna por la producción total: A= Calculamos la matriz de Leontief: 3 universoexacto.com L=I –A= La nueva producción total la calculamos con la ecuación matricial (I – A)X = D, siendo D= la nueva demanda final. Como queremos averiguar la nueva producción total, X, la despejamos: X = (I – A)-1D Entonces debemos calcular la matriz inversa de Leontief. (I – A)-1 = (1/|I – A|)·(adj (I – A))t Primero calculamos el determinante |I – A| = = — Para calcular la matriz transpuesta de la adjunta en una matriz de orden 2x2, simplemente intercambiamos los elementos de la diagonal principal y le cambiamos el signo a los elementos de la diagonal secundaria. (adj (I – A))t = Por lo tanto, (I – A)-1 = Finalmente, X = (I – A)-1D = = Acabamos de obtener la nueva producción total, es decir que, S1 debe producir 230 y S2 debe producir 120. Ahora vamos a construir la nueva tabla. Recordemos que la matriz que nunca cambia es la matriz de coeficientes tecnológicos, A, mientras que la matriz insumo-producto cambió al cambiar la demanda final. Sabemos que: S1 4 DF PT S1 42 230 S2 28 120 universoexacto.com S2 VA PT --230 120 --- Necesitamos calcular la nueva matriz insumo-producto, para ello multiplicamos las columnas de la matriz A por los nuevos valores de producción total. A= B= S1 S2 DF PT S1 92 96 42 230 S2 92 0 28 120 VA 46 24 70 --- PT 230 120 --- 350 230 – (92 + 92) = 46 5 universoexacto.com 120 – (96 + 0) = 24 Totales obtenidos de sumar las filas o las columnas.











