Inductores
Anuncio

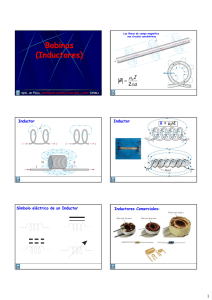
Las líneas de campo magnético son círculos concéntricos Bobinas (Inductores) B = μo I 2π a Dpto. de Física. Facultad de Ciencias FísicoFísico-Mat. y Nat. (UNSL) Inductor Símbolo eléctrico de un Inductor Inductor B = μ0nI Inductores Comerciales: 1 Ley de Faraday: B - Tensión Autoinducida - + I ε = −N + Tensión Autoinducida i(t) - + La INDUCTANCIA es la propiedad que tiene todo conductor, de oponerse a que la corriente eléctrica cambie, generando una tensión inducida que se opone al cambio que la produce. (Ley de Lenz) ∆ΦB ΦB ~ i(t) di(t) ε = -(KN) ∆t ΦB =Ki(t) dt Tensión Autoinducida di (t ) ε = −L dt L=(KN) L es la AUTOINDUCTANCIA del Inductor ó simplemente INDUCTANCIA L se mide en Henry (H) ε = −L di (t ) dt H = s.Volts/A Joseph Henry Henry:: (1797 17971878)) 1878 Físico y Matemático estadunidense.. Fue el estadunidense primer director del Instituto Smithsonian Smithsonian.. Características de los inductores: La Inductancia sólo depende de factores geométricos y del material.. material L= N 2μ A l 2 Características de los inductores: Características de los inductores: Comportamiento de un Inductor en Continua Combinación de Inductores en Serie: L1 v1 = L1 L2 L3 i di di di v2 = L2 v3 = L3 dt dt dt Ln vn = Ln vTotal = v1 + v2 + v3 + ...vn = (L1 + L2 + L3 + ...Ln ) v =L di dt di dt di (t ) dt * La i no puede cambiar en forma instantánea en un inductor En Continua un Inductor se comporta p como un corto circuito Lequivalente = L1 + L2 + L3 + … Ln i ≡ LEquivalente Energía Almacenada en el campo magnético del Inductor: Energía Almacenada en el campo magnético del Inductor: p(t)=v(t) (t)=v(t)ii(t) p(t)=d (t)=dw w(t)/dt v(t)=Ldii(t)/dt v(t)=Ld dw(t)/d(t)=L (t)/d(t)=Lii(t)d (t)dii(t)/dt w(t)= (t)=½L ½Lii2(t) 3 Circuitos RL: i Estado Estacionario V0 - VL(t) – VR(t) = 0 VL(t) = Ld Ldii(t)/dt V0 VR((t)) = i((t)R ) Estado Transitorio V0 - Ld Ldii(t)/dt (t)/dt- i(t)R = 0 t/ττ) i(t)= V0/R( /R(1 1-e-t/ 100% 95% Vfinal 0 t Inductor voltage after switch c losure Iinitial R L 63% 60% t 98% 99% t/ττ) i(t)= V0/R( /R(1 1-e-t/ τ = L/R 40% 37% 20% 0 Current after switch closure t/ττ) VL(t)=V0e-t/ 86% 80% Percen nt of final value Cuando un inductor es conectado en serie con una resistencia y una fuente de tensión continua: τ = L/R t/ττ) VL(t)=V0e-t/ 14% 5% 0 0 1τ 2% 2τ 3τ 4τ Number of time constants 1% 5τ Capacitor:: es un par de conductores con Capacitor Capacitores (Condensadores) cargas de igual magnitud pero signos opuestas Definición de Capacidad Capacidad:: C=Q/∆V La capacitancia de un capacitor es la cantidad de carga que puede almacenar por unidad de Tensión Tensión. Unidad [Faraday]=[ araday]=[C Cuolombs]/[ uolombs]/[V Volts] Dpto. de Física. Facultad de Ciencias FísicoFísico-Mat. y Nat. (UNSL) 4 Combinación de capacitores capacitores:: Energía Almacenada en un capacitor cargado C = Q/∆V Qtotal = Q1 C = Q/∆V dW= ∆V ∆Vdq dq = (q/C q/C)dq )dq Paralelo + Q2 CEquiv∆V= C1∆V + C2∆V CEquivalente = C1 + C2 W = Q2/2C U= Q2/2C = Q∆V/ ∆V/2 2 = C∆V2/2 360 Joules en 2 ms ms.. Serie 3000 ∆V= ∆V1 + ∆V2 Veces de la Q/CEquiv = Q/C1+Q/C2 potencia una 1/CEquiv=1/C1+1/C2 Lamparita de 60 W! Comportamiento de los Capacitores en Continua. Continua. Q = C∆V Estado Estacionario ∆Q/∆t = C∆V/∆t I = CdV/dt En Continua, un capacitor se comporta como un circuito abierto ≡ Transitorios en circuitos RC RC:: Carga de un Capacitor ε - VC(t) – VR(t) = 0 VC(t) = q(t)/C Estado Transitorio ε - q(t)/C – Rdq(t)/dt = 0 q(t) = εC( C(1 1-e-t/(RC)) VR(t) = i(t)R t/ττ) q(t) = QMáx(1 (1-e-t/ QMáx=εC τ = RC i(t) t/ττ) = ε(1-e-t/ t/ττ) VC(t) = (QMáx/C)( /C)(1 1-e-t/ ε - q(t)/C – i(t)R = 0 i(t) = dq(t)/dt ε - q(t)/C – Rdq(t)/dt = 0 i(t) = dq(t)/dt t/ττ =(ε/R t/ττ i(t) = IMáxe-t/ /R)) e-t/ 5 Ejemplo: ε=12 V Qmáx= R= 800 kΩ kΩ = 8x105 Ω t/ττ) q(t) = QMáx(1 (1-e-t/ C= 5 μF = 5x10-6F q(t=ττ) = QMáx(1 q(t= (1-e-τ/τ) Qmáx =εC= ((12V)(5x10 (12V)( V)(5 V)(5 5x10-6μF) q(t=ττ) = Qmáx(0.63) q(t= = 60x10-6C = 60μ 60μC τ = RC RC = )(5x10 5x10-6μF)= 4s (8x105Ω)( t=5 t= 5τ t/4 4) [mC] q(t) = 60(160(1-e-t/ t=ττ t= IMáx= ε= t/ττ =(ε/R t/ττ i(t) = IMáxe-t/ /R)) e-t/ i(t=ττ)= Imáx(0.37) i(t= 37) t/ττ) VC(t) = ε(1-e-t/ t=ττ t= Transitorios t=ττ t= Estacionario 6 Transitorios en circuitos RC RC:: Descarga de un Capacitor ε - q(t)/C – i(t)R = 0 -q(t)/C – Rdq(t)/dt = 0 t/ττ VC(t) =εe-t/ t/ττ) q(t) = QMáx(e-t/ t/ττ i(t) = -IMáxe-t/ Resumen: Resumen: Inductores y Capacitores t/ττ) i(t)=(V0/R)( /R)(1 1-e-t/ t/ττ VL(t)=V0e-t/ R, L y C sólo dependen de factores geométricos y I = t/ττ VL(t)= (t)=-V0e-t/ t/ττ i(t)= ( ) (V0/R (t)=( /R))e-t/ t/ττ i(t)= ( ) -(V0/R (t)=/R))e-t/ t/ττ) VC(t)=V0(1-e-t/ t/ττ VC(t)=V0e-t/ τ=RC Estado Transitorio. material.. material No Dependen ni de V ni de I ni de q t/ττ i(t)=(V0/R)e-t/ τ =L/R del iL (t ) = 1 VR R t =t L ∫t =0 iC (t ) = C VR = IR νL (t )dt dvC (t ) dt vL (t ) = L vC (t ) = 1 C di (t ) dt t =t ∫t =0 iC (t )dt Válidas para todo tiempo 7 iL(t)= (t)=5 5(t (t-2) 2<t< <t<4 4 iL(t)= (t)=5 5(t (t-2) 2<t< <t<4 4 iL(t)= (t)=0 0 iL(t)= (t)=-2(t (t-4)+ )+10 10 4<t< <t<10 10 0<t< <t<2 2 L = 4mH iL(t)= (t)=0 0 0<t< <t<2 2 vL(t)=L (t)=L5 5 2<t< <t<4 4 iL(t)= (t)=-2(t (t-4)+ )+10 10 4<t< <t<10 10 di (t ) vL (t ) = L dt vL(t)=L (t)=L5 5 2<t< <t<4 4 (t)=0 0 vL(t)= vL (t ) = L di (t ) dt vL(t)= (t)=-L2 4<t< <t<10 10 vL(t)= (t)=-L2 4<t< <t<10 10 Ejemplo Que pasaría con señales senoidales? 8